버블 정렬 (Bubble sort)

bubble sort.gif

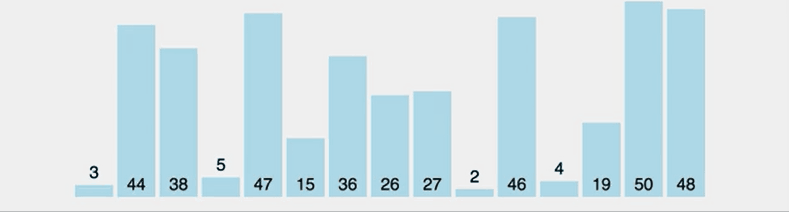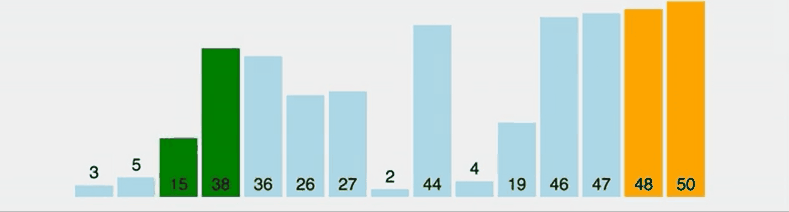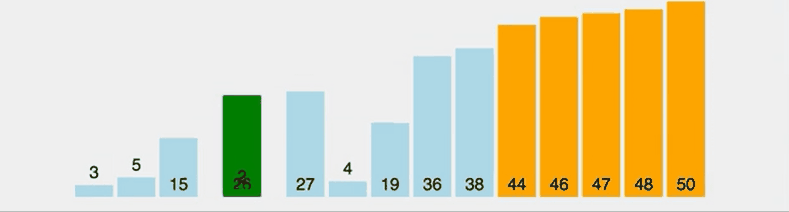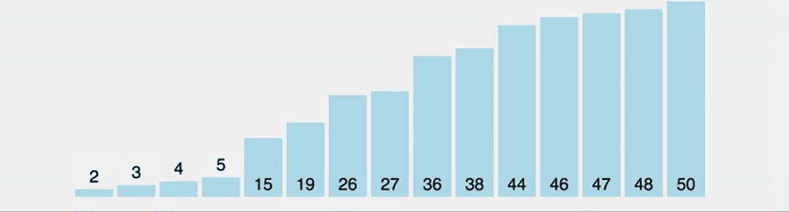
버블 정렬은 서로 이웃한 두 노드의 크기를 비교한 뒤 결과에 따라 교환을 반복하는 알고리즘으로 단순 교환정렬이라고도 부른다. 버블 정렬은 옆에 있는 노드끼리만 교환하므로 안정적인 정렬이다. 버블정렬은 정렬 알고리즘 중에서 가장 간단하지만 매우 비효율적인 알고리즘이다.

버블 정렬은 목록이 이미 정렬되어 있어도 모든 항목을 검사하기때문에 O(N²)의 시간 복잡도를 가진다.

def bubble_sort(li):
  length = len(li) - 1

  for i in range(length):
    for j in range(length - i):
      if li[j] > li[j+1]:
        li[j], li[j+1] = li[j+1], li[j]
  return li

삽입 정렬 (Insertion sort)

insertion sort.gif

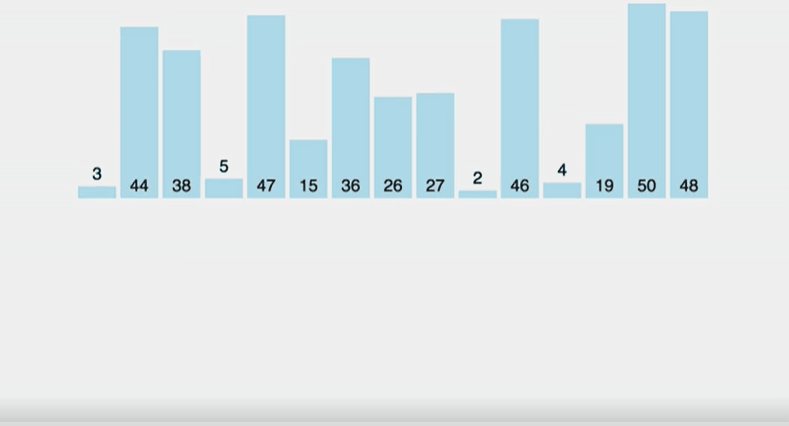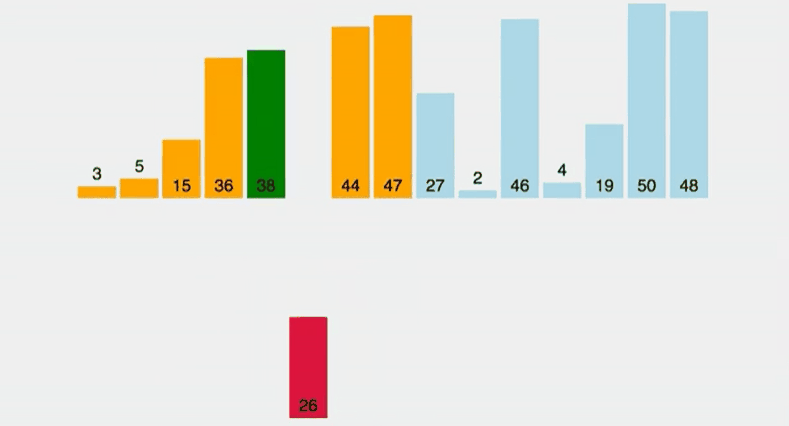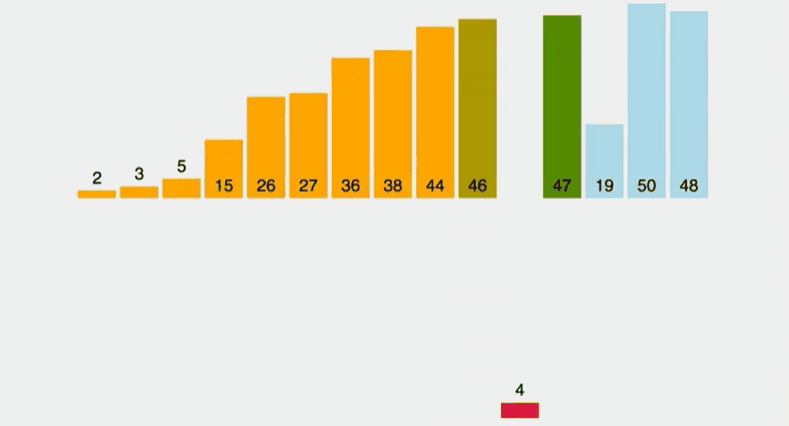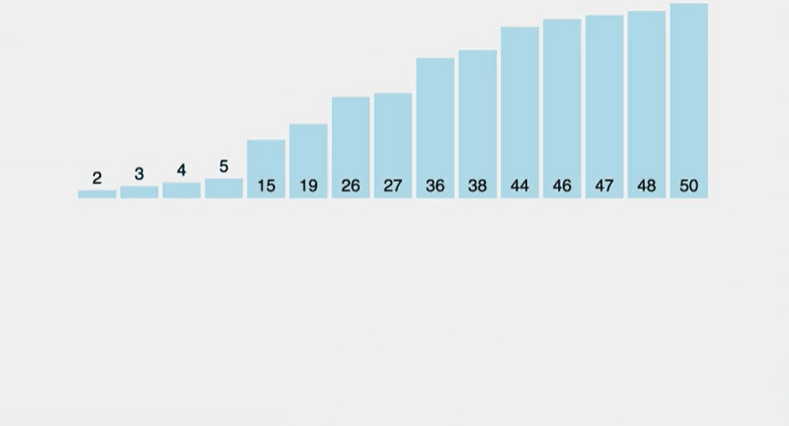
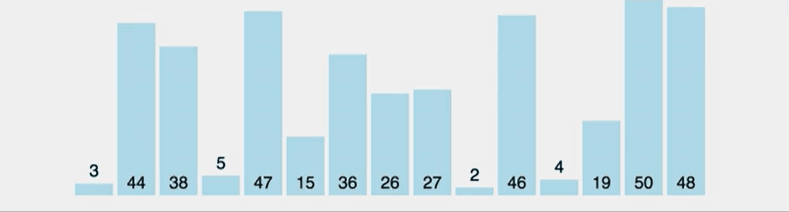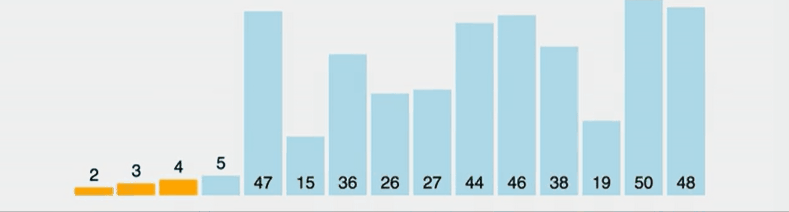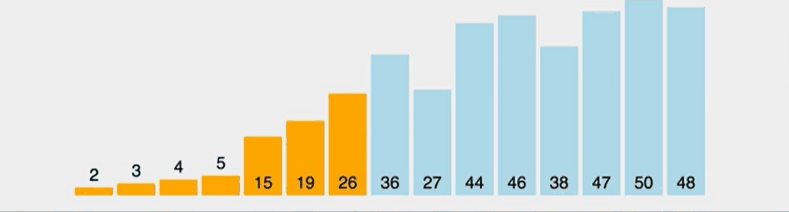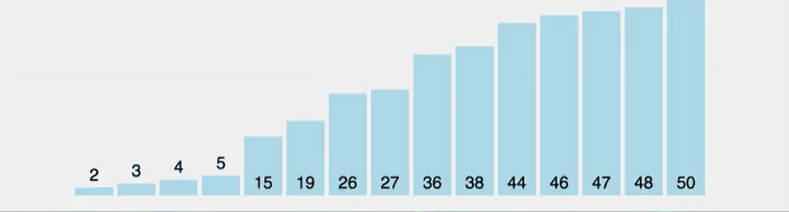
삽입 정렬은 아직 정렬되지 않은 노드와 정렬된 노드의 값을 비교해 값이 더 큰 노드의 인덱스보다 작은 인덱스에 삽입해가며 정렬하는 알고리즘이다. 선택 정렬과 비슷해보이지만 선택 정렬은 가장 작은 데이터를 선택하지만 삽입 정렬은 그렇지 않다는 차이점이 있다.

만약 삽입 정렬을 실시할 리스트가 이미 정렬된 경우에는 코드 수행 시간이 오래 걸리지 않으며 시간 복잡도가 O(N)이 되지만 내림차순으로 이미 정렬되어 있는 리스트를 오름차순으로 재정렬하려면 반복문으로 오름차순으로 정렬될때까지 수행해야하기 때문에 시간 복잡도가 O(N²)가 된다.

def insertion_sort(li):
  for i in range(1, len(li)):
    j = i - 1
    key = li[i]
    while li[j] > key and j >= 0:
      li[j+1] = li[j]
      j -= 1
    li[j+1] = key
  
  return li

선택 정렬 (Selection sort)

selection sort.gif

선택 정렬은 정렬할 데이터 중 가장 작은 데이터를 선택한 뒤 맨 앞부터 순서대로 정렬하는 알고리즘이다. 루프문을 통해서 모든 인덱스에 접근해야하고, 최소값을 찾게 되면 현재 인덱스와 최소값을 서로 스왑해야하기 때문에 O(N²)의 시간 복잡도를 가진다.

def selection_sort(li):
  for i in range(len(li) - 1):
    mid = i
    for j in range(i + 1, len(li)):
      if li[j] < li[mid]:
        mid = j
    if mid != i:
      li[i], li[mid] = li[mid], li[i]

  return li