학습률
학습률은 매 가중치에 대해 구해진 기울기 값을 얼마나 경사 하강법에 적용할지 결정하는 하이퍼파라미터이다.

위의 식에서 학습률은 얼마나 이동할지를 조정하는 하이퍼파라미터이다. 경사 하강법이 산을 내려가는 과정이라면 학습률은 보폭을 결정하게 된다. 학습률이 크다면 산을 내려가는 보폭이 커져서 성큼성큼 이동하게 되고, 학습률이 작다면 산을 내려가는 보폭이 작아져서 조심조심 이동하게 된다.
산을 내려가는 보폭이 작아서 너무 천천히 내려오게 된다면 날이 어두워져서 산을 내려오는데 문제가 생길 것이고, 산을 내려가는 보폭이 크다면 서둘러서 내려가려고 하다보니 발을 잘못 디뎌서 다치게 될 수도 있다.
이와 같이 학습률이 너무 낮으면 최적점에 이르기까지 너무 오래 걸려서 주어진 Iteration 내에서 최적점에 도달하는 것에 실패할 수도 있다. 반대로 학습률이 너무 높다면 경사 하강 과정에서 발산하게 되면서 모델이 최적값을 찾을 수 없게 되어버린다.
이러한 문제를 해결하기 위해서 사용되는 방법이 바로 학습률 감소/계획법이다.
학습률 감소 (Learning rate Decay)
학습률 감소는 Adagrad, RMSProp, Adam과 같은 주요 옵티마이저에 이미 구현되어 있기 때문에 쉽게 적용할 수 있다. 해당 옵티마이저의 하이퍼파라미터를 조정하면 감소 정도를 변화시킬 수 있다.
model.compile(optimizer = tf.keras.optimizer.Adam(
lr=0.001, # 학습률
beta_1=0.89, # 0보다 크고 1보다 작은 float 값. (공식 문서 참고)
loss='sparse_categorical_crossentropy',
metrics=['accuracy'])위의 코드와 같이 .complie 내에 있는 optimizer= 에 옵티마이저를 적용한 후 내부 하이퍼파라미터를 변경하면 학습률을 감소시킬 수 있다.
학습률 계획법 (Learning rate Scheduling)
학습률 계획은 다음과 같이 .experimental 내부의 함수를 사용해 설계할 수 있다.
first_decay_steps = 1000
initial_learning_rate = 0.01 # 초기 학습률
lr_decayed_fn = (
tf.keras.experimental.ConsineDecayRestarts(
initial_learning_rate,
first_decay_steps))
model.complie(optimizer=tf.keras.optimizers.Adam(
learning_rate=lr_decayed_fn,
loss='sparse_categorical_crossentropy',
metrics=['accuracy'])가중치 초기화 (Weight Initialization)
가중치 초기화는 초기 가중치 설정과 관련된 신경망에서 매우 중요한 요소이다.
Xavier 초기화 (Xavier initialization)
Xavier 초기화는 가중치를 표준편차가 고정값인 정규 분포로 초기화 했을 때의 문제점을 해결하기 위해 등장한 방법이다.
Sigmoid 함수를 사용했을 경우에는 Xavier 초기화를 사용하는 것이 유리하기 때문에 주로 Xavier 초기화를 사용해준다.
Xavier 초기화는 표준편차가 루트 1/n인 정규분포를 따르도록 가중치를 초기화 시켜준다.
He 초기화 (He initialization)
Xavier 초기화는 Sigmoid 함수가 활성화 함수로 설정된 신경망에서는 잘 작동하지만 ReLU 함수의 경우는 층이 지날수록 활성값이 고르지 못하다는 문제를 갖고 있다. 이러한 문제를 해결하기 위해 나타난 것이 바로 He 초기화이다.
He 초기화는 표준편차가 루트 2/n인 정규분포를 따르도록 가중치를 초기화 시켜준다.
과적합을 방지하는 방법
Weight Decay (가중치 감소)
과적합을 방지할 수 있는 방법 중 하나는 바로 가중치를 감소시키는 것이다.
과적합을 가중치의 값이 클 때 주로 발생하므로 가중치가 너무 커지지 않도록 손실 함수에 조건(=가중치와 관련된 항)을 추가하는 것이다.
조건을 어떻게 적용할지에 따라서 L1 Regularization(LASSO)와 L2 Regularization(Ridge)로 나뉘며 식은 아래와 같다.

위의 식에서 람다(λ)의 값을 조절해서 가중치를 조절한다. 람다의 값이 커지면 규제가 강해지므로 기울기가 완만하게 변하고, 람다의 값이 작아지면 규제가 약해지므로 기울기가 급격하게 변한다.
여기서 L1(LASSO)는 규제가 강해진다면 0이 될 수 있지만, L2(Ridge)는 규제가 강해진다고 해도 0에 가까워질 뿐이지 0이 될 수는 없다는 차이를 가지고 있다.
람다의 값이 0이 된다면 학습이 잘 되지 않으므로 L1보다는 L2를 선호하는 경향이 있다고 한다.
Dense(64,
kernel_regularizer = regularizers.l2(0.01),
activity_regularizer = regularizers.l1(0.01))Dropout
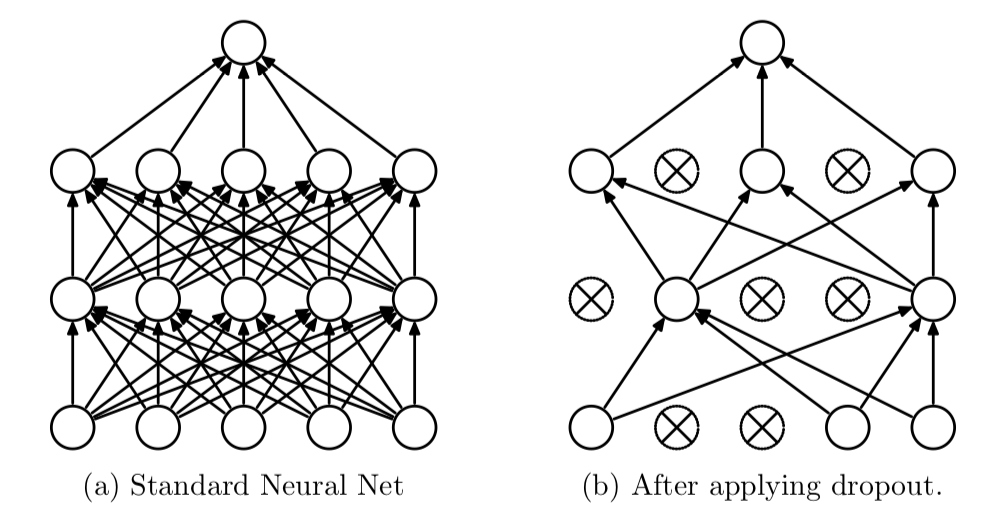
Dropout은 Iteration마다 레이어 노드 중 일부를 사용하지 않고 학습을 진행하는 방법이다.
Dropout을 사용하면 매 Iteration마다 다른 노드가 학습되면서 전체적인 가중치가 과적합 되는 것을 방지할 수 있다.
Dense(64,
kernel_regularizer = regularizers.l2(0.01),
activity_regularizer = regularizers.l1(0.01))
Dropout(0.5) # 50%의 노드만 사용해서 학습할게!위의 코드와 같이 Dropout은 사용하고 싶은 층 바로 다음에 Dropout 함수를 추가해주면 된다. 이때 Dropout 함수의 파라미터로 들어가는 것은 0~1 사이의 실수로 지정하려는 레이어 내의 노드 연결을 입력한 비율만큼 강제로 끊는다.
이때 꺼지는 노드는 Iteration마다 랜덤이며 Dropout은 학습할 때만 사용되고 출력할 때는 사용되지 않는다.
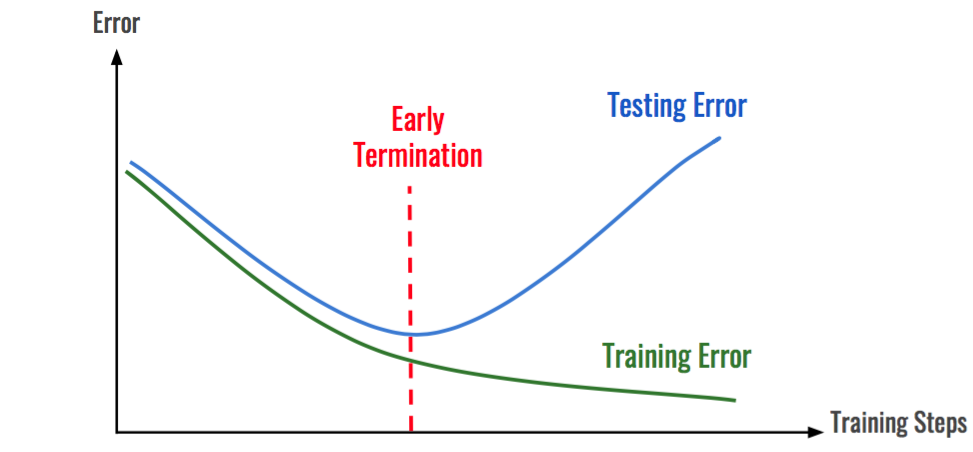
Early Stopping (조기 종료)
조기 종료는 학습(Train) 데이터에 대한 손실은 계속해서 줄어들지만 검증(Validation) 데이터셋에 대한 손실은 증가하면 학습을 종료하도록 설정하는 방법이다.
early_stop = keras.callbacks.EarlyStopping(
monitor='val_loss', # 'val_loss' 값 살펴볼거야
min_delta=0,
patience=5, # val_loss 값이 제일 작은
# Epoch로부터 5가 지날때까지 감소하지 않으면 멈춰!
verbose=1)
model.fit(X_train, y_train, # 훈련 데이터셋
batch_size = batch_size,
epochs = 30, # 30번 반복할거야!
verbose = 1,
validation_data=(X_test, y_test), # 검증 데이터셋
callbacks=[early_stop, save_best])
# early_stop = 조기종료 할거야
# save_best = Best 모델 저장해줘위의 코드를 돌리면 다음과 같은 결과를 얻을 수 있다.

결과를 해석해보자면, val_loss의 값은 Epoch 1일때가 제일 작은 값인 0.7761이 나오는데 5번이 지났 Epoch 6까지 0.7761 이하의 값이 나오지 않았으므로 해당 모델의 학습을 조기종료시킨 것이다. 굳이 val_loss 값을 살펴보지 않아도 알 수 있는 방법이 있는데 바로 바로 윗줄에 있는 "val_loss improved from inf 0.77609" 부분을 살펴보면 된다.
val_loss의 값이 줄어들었으면 improved가 줄어들지 않았으면 did not improve가 뜨므로 쉽게 값이 줄어들었는지 아닌지를 알 수 있다.
