Activity-selection algorithm

Activity-selection 정의

• 활동 선택 알고리즘은 그리디 알고리즘의 일정으로 스케쥴링과 관련된 알고리즘이다.
• 특정 시간내에 많은 활동을 할 수 있는 최적의 방법을 찾는 방법이다.

상세 설명

BOJ 1931

• 활동을 모아둔 집합 $S = \{a_1, a_2, \dots, a_n\}$ 이 있고, 원소 $a_{i}$ 는 각 활동시간을 표현함
• 각 활동 $a_{i}$ 는 시작시간 $s_{i}$ 와 종료시간 $f_{i}$ 을 가지고 있음
• 시작 시간과 종료 시간은 $0 \leq s_i < f_i \leq \ \infty$ 의 영역에 존재한다.

1. 입력 표현

• 만약 11개의 a를 입력받았다고 하면 아래와 같이 표현이 가능 함
  $\begin{array}{c|ccccccccccc} i & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11 \\ \hline s_i & 1 & 3 & 0 & 5 & 3 & 5 & 6 & 8 & 8 & 2 & 12 \\ f_i & 4 & 5 & 6 & 7 & 9 & 9 & 10 & 11 & 12 & 14 & 16 \\ \end{array}$

2. 종료시간 기준으로 오름차순 정렬

• 위의 테이블을 종료시간 기준으로 오름차순을 정리하면 다음과 같다.
• 백준의 문제 같은 경우에는 예시가 종료시간을 오름차순으로 입력받았기 때문에 변화가 없음

3. 부분 문제 선정

• 중복없는 부분 집합을 만들기 위해서는 구간의 중복없이 가장 빨리 끝나는 회의를 찾으면 된다.

• 이미 종료 시간을 기준으로 회의를 오름차순으로 정렬 해뒀기 때문에 인덱스 i를 탐색하면서 아래의 조건에 맞는 회의를 찾는다.

  $s_i >= f_{k}$

  k는 부분탐색 조건을 만족할 때 선택된 회의의 인덱스를 의미함

• 이를 활용하여 의사 코드를 나타내면 아래와 같음
  
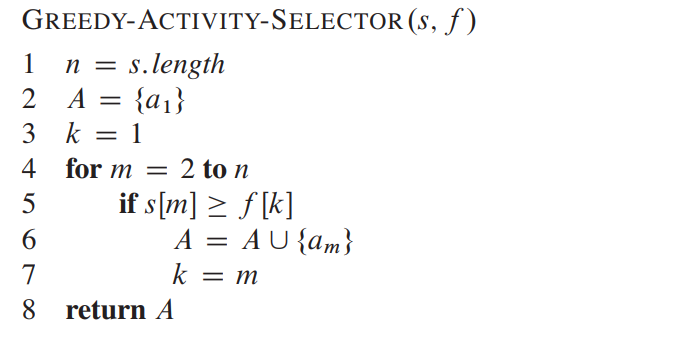
  출처: Introduction to Algorithms, Third Edition

python 구현

import sys

N = int(input())
reservation = []
for i in range(N):
    A, B = list(map(int,sys.stdin.readline().split()))
    reservation.append([A,B])

reservation.sort(key=lambda x: (x[1], x[0]))
#print(reservation)

k = 0
cnt = 1

#start 조건 찾기

for i in range(1,N):
    if(reservation[i][0] >= reservation[k][1]):
        cnt += 1
        k = i



print(cnt)