LCS Algoritm

Mechboy·2024년 7월 28일

String algoritm python

Algorithm

목록 보기

4/5

Longest Common serise

LCS 정의

LCS는 두 수열이 주어졌을때 공통으로 존재 하는 가장 긴 부분 수열을 만드는 알고리즘
이때 각 원소들이 연속해서 근접 하지 않아도 된다.

구현 방법

BOJ 17218

BOJ 17218 문제의 풀이 방법을 기준으로 설명

두 문장을 입력 받아 가장 가장큰 부분 문자열을 찾는 문제
-. 입력으로 비교할 문장을 Sentense_A, Sentense_B로 정의 한다.
-. Row = len(Sentense_B) , col = len(Sentense_A)인 2차원 리스트를 생성하여 각 문자열의 원소값을 비교

우선 Sentence_B의 각문자열의 원소들을 Sentence_A의 원소와 하나씩 비교를 진행한다

0. Sentense_B[0] = 0

\begin{array}{c|cccccccccccc} & 0 & A & U & T & A & B & B & E & H & N & S & A \\ \hline 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ \end{array}

1. Sentense_B[1] = B

\begin{array}{c|cccccccccccc} & 0 & A & U & T & A & B & B & E & H & N & S & A \\ \hline 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ B & 0 & 0 & 0 & 0 & 0 & 1 & 1 & 1 & 1 & 1 & 1 & 1 \\ \end{array}

Sentense_A[5] 일때 똑같은 문자 B가 존재하기 때문에 해당 위치부터 마지막까지 +1을 해준다.
Sentense_A[6] 일때 똑같은 문자 B가 존재하지만, Sentense_A[5] 일때 카운팅을 해줬기 때문에 카운트를 해주지 않음

2. Sentense_B[2] = C

\begin{array}{c|cccccccccccc} & 0 & A & U & T & A & B & B & E & H & N & S & A \\ \hline 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ B & 0 & 0 & 0 & 0 & 0 & 1 & 1 & 1 & 1 & 1 & 1 & 1 \\ C & 0 & 0 & 0 & 0 & 0 & 1 & 1 & 1 & 1 & 1 & 1 & 1 \\ \end{array}

Sentense_A에서 C가 존재하지 않기 때문에 윗줄과 똑같은 값을 가진다.

3. Sentense_B[3] = U

\begin{array}{c|cccccccccccc} & 0 & A & U & T & A & B & B & E & H & N & S & A \\ \hline 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ B & 0 & 0 & 0 & 0 & 0 & 1 & 1 & 1 & 1 & 1 & 1 & 1 \\ C & 0 & 0 & 0 & 0 & 0 & 1 & 1 & 1 & 1 & 1 & 1 & 1 \\ U & 0 & 0 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 \\ \end{array}

Sentense_A[2]에서 똑같은 문자 U가 존재하기 때문에 해당 위치에 인덱스 4까지 +1을 가산해준다.
Sentense_A[5] 일때 테이블값이 1을 가지고 있지만 이미 앞쪽영역에서 1을 갱신해줬기 때문에 가산을 해주지 않음

4. Sentense_B[4] = A

\begin{array}{c|cccccccccccc} & 0 & A & U & T & A & B & B & E & H & N & S & A \\ \hline 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ B & 0 & 0 & 0 & 0 & 0 & 1 & 1 & 1 & 1 & 1 & 1 & 1 \\ C & 0 & 0 & 0 & 0 & 0 & 1 & 1 & 1 & 1 & 1 & 1 & 1 \\ U & 0 & 0 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 \\ A & 0 & 1 & 1 & 1 & 2 & 2 & 2 & 2 & 2 & 2 & 2 & 2 \\ \end{array}

Sentense_A[1]에서 똑같은 문자 A가 존재하기 때문에 해당 위치에 +1을 해준다.
Sentense_A[2] 일때 테이블값이 1을 가지고 있지만 이미 앞쪽영역에서 1을 갱신해줬기 때문에 가산을 해주지 않음
Sentense_A[4] 일때 똑같은 문자 A가 존재 하고 테이블 바로 왼쪽에도 값을 가지고 있기 떄문에 해당 위치에 마지막 인덱스까지 +1을 가산해준다.

여기서 자세히 보면 아래와 같은 규칙을 확인 할 수 있음

$Sentense_A[i] = Sentense_B[j]$ 를 만족 하는 경우에는 아래의 값을 가지게됨

$LCS_{test}[j,i] = LCS_{test}[j-1,i-1] + 1$

$Sentense_A[i] \neq Sentense_B[j]$ 인 경우

$LCS_{test}[j,i] = max(LCS_{test}[j-1,i],LCS_{test}[j,i-1] )$

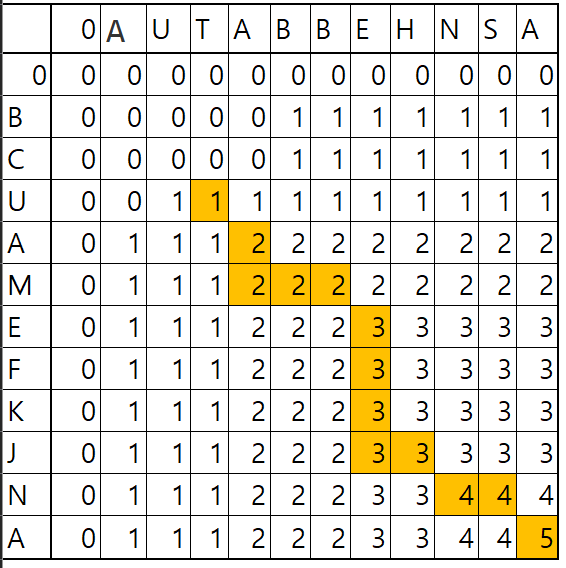
위조건에 맞춰서 테이블 채우면 아래와 같이 표현이 가능하다.

\begin{array}{c|cccccccccccc} & 0 & A & U & T & A & B & B & E & H & N & S & A \\ \hline 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ B & 0 & 0 & 0 & 0 & 0 & 1 & 1 & 1 & 1 & 1 & 1 & 1 \\ C & 0 & 0 & 0 & 0 & 0 & 1 & 1 & 1 & 1 & 1 & 1 & 1 \\ U & 0 & 0 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 \\ A & 0 & 1 & 1 & 1 & 2 & 2 & 2 & 2 & 2 & 2 & 2 & 2 \\ M & 0 & 1 & 1 & 1 & 2 & 2 & 2 & 2 & 2 & 2 & 2 & 2 \\ E & 0 & 1 & 1 & 1 & 2 & 2 & 2 & 3 & 3 & 3 & 3 & 3 \\ F & 0 & 1 & 1 & 1 & 2 & 2 & 2 & 3 & 3 & 3 & 3 & 3 \\ K & 0 & 1 & 1 & 1 & 2 & 2 & 2 & 3 & 3 & 3 & 3 & 3 \\ J & 0 & 1 & 1 & 1 & 2 & 2 & 2 & 3 & 3 & 3 & 3 & 3 \\ N & 0 & 1 & 1 & 1 & 2 & 2 & 2 & 3 & 3 & 4 & 4 & 4 \\ A & 0 & 1 & 1 & 1 & 2 & 2 & 2 & 3 & 3 & 4 & 4 & 5 \\ \end{array}

최종적으로 우측 제일 하단을 보면 공통으로 존재 하는 값이 공동으로 존재하는 가장 큰 원소 값이다.

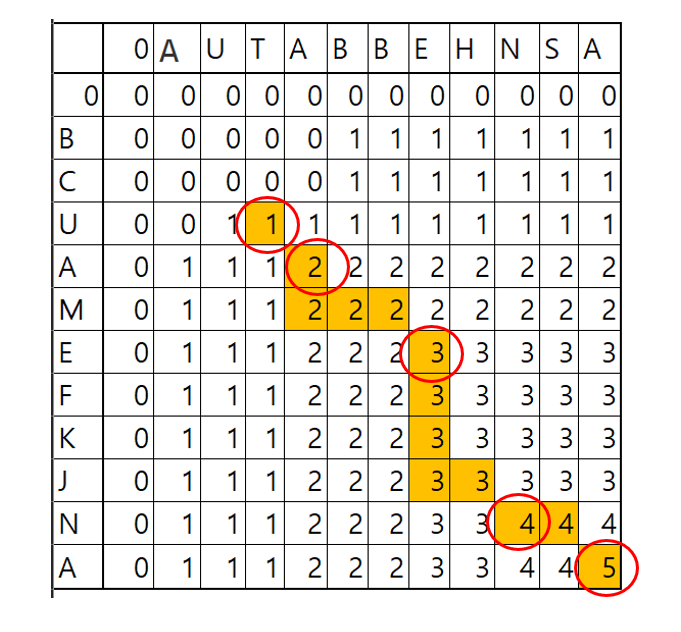
계산방법

만약 공통으로 존재하는 수열을 찾기 위해서는 우측 하단을 기준으로 아래의 조건에 맞춰서 각 원소를 찾으면된다.

확인하려는 원소값과 좌측, 상단의 원소가 똑같을 경우
$LCS_{test}[j,i] = LCS_{test}[j-1,i] = LCS_{test}[j,i-1]$
위의 조건을 만족 하는 경우에는 좌표 포인터를 좌측으로 옮긴다.

확인하려는 원소값-1 과 좌측, 상단의 원소가 똑같을 경우
$LCS_{test}[j,i]-1 = LCS_{test}[j-1,i] = LCS_{test}[j,i-1]$
위의 조건을 만족 하는 경우에는 좌표 포인터를 좌측상단으로 옮긴다.

$LCS_{test}[j,i]-1 = LCS_{test}[j,i-1]$
$LCS_{test}[j,i] = LCS_{test}[j-1,i]$
위의 조건을 만족 하는 경우에는 좌표 포인터를 상단으로 이동한다.

코드구현

import sys

sentense_A = "0"+sys.stdin.readline().strip()
sentense_B = "0"+sys.stdin.readline().strip()

N = len(sentense_A) #coloum
M = len(sentense_B) #row

LCS_test = [[0]*(N) for _ in range(M)]

for i in range(1,M):
    for j in range(1,N):
        if sentense_B[i] == sentense_A[j]:
            LCS_test[i][j] = LCS_test[i-1][j-1] + 1
        else:
            LCS_test[i][j] = max(LCS_test[i-1][j],LCS_test[i][j-1]) 

#for k in range(M):
#    print(LCS_test[k])   

A_pointer = N-1
B_pointer = M-1
value = LCS_test[i][j]

result = []

while value != 0:

    A_test = LCS_test[B_pointer][A_pointer-1]
    B_test = LCS_test[B_pointer-1][A_pointer]
    #print(A_pointer,B_pointer)
    if (A_test== B_test) :
        if A_test == value:
            B_pointer -= 1
            continue
        elif A_test == (value-1):
            #print(sentense_B[B_pointer]) 
            result.append(sentense_B[B_pointer])
            A_pointer -= 1
            B_pointer -= 1
            value -= 1
    elif A_test > B_test:
        A_pointer -= 1
    elif A_test < B_test:
        B_pointer -= 1
           


print(''.join(reversed(result)))