2차 digital filter 설계

기본적으로 2차 필터를 활용해서 DSP 필터 설계를 많이함. 보통 그이유는 아날로그 필터설계에서도 대표적으로 많이 활용되는것이 2차 필터모델이며 고차수의 필터모델을 설계할때에도 필터를 직렬로 연결하는 방법을 활용하기 때문임. 더 나아가 연속함수의 s공간에서 설계된 필터도 Bilinear 변환을 통해서 z공간으로 이산공간으로 변환이 가능하기 때문에 디지털과 아날로그 간의 이동이 편한점도 한 몫한다고 봐도 됨.

The Biqud

• 기본적으로 신호처리 영역에서 필터를 구현한다는 것은 아래 영역에서 필터계수 b와 a를 구하는것임

  $y_n=b_0 x_n+b_1 x_{n-1}+b_2 x_{n-2}-a_1 y_{n-1}-a_2 y_{n-2}$
  $y:$ 출력값, -1,-2는 이전 샘플을 의미함
  $x:$ 입력값, -1,-2는 이전 샘플을 의미함

• 그리고 더 나아가 해당 식을 Z변환을 해주면 아래와 같은 전달함수를 얻을 수 있음

  $H(z) = \frac{b_0+b_1 z^{-1}+b_2 z^{-2}}{1+a_1 z^{-1}+a_2 z^{-2}}$

• 필터설계에서는 이 전달함수에서 영점과 극점의 계산을 통해서 필터의 성격을 결정짓는다고 생각하면 된다
  

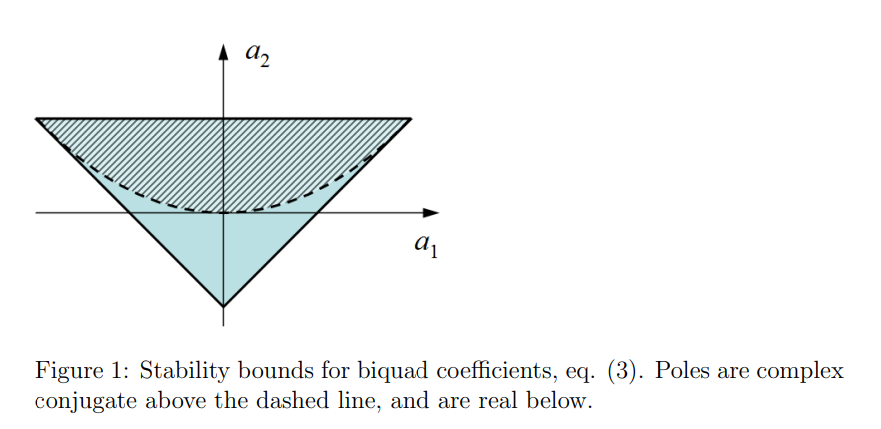
The Biqud

• 기본적으로 신호처리 영역에서 필터를 구현한다는 것은 아래 영역에서 필터계수 b와 a를 구하는것임

  $y_n=b_0 x_n+b_1 x_{n-1}+b_2 x_{n-2}-a_1 y_{n-1}-a_2 y_{n-2}$
  $y:$ 출력값, -1,-2는 이전 샘플을 의미함
  $x:$ 입력값, -1,-2는 이전 샘플을 의미함

• 그리고 더 나아가 해당 식을 Z변환을 해주면 아래와 같은 전달함수를 얻을 수 있음

  $H(z) = \frac{b_0+b_1 z^{-1}+b_2 z^{-2}}{1+a_1 z^{-1}+a_2 z^{-2}}$

• 필터설계에서는 이 전달함수에서 영점과 극점의 계산을 통해서 필터의 성격을 결정짓는다고 생각하면 된다
  

Bilinear transforms

• bilinear transforms 이란 S공간에 있는 변수를 Z공간의 변수로 이동하는것을 의미함.

$H(s) = \frac{b_2+b_1 s^{1}+b_0 s^{2}}{a2+a_1 s^{1}+a_2 s^{2}}$

의 S공간의 전달함수에

$s = \frac{2}{T}\frac{1-z^{-1}}{1+z^{-1}}$

를 대입하여 z 공간으로 대입시켜 준다. 이때 T는 (1/fs) 로 샘플링레이트의 역수

• 여기서 s에다가 무식하게 대입해서 전부 계산하면 아래와같이 z공간에서의 전달 함수를 구할 수 있음
  

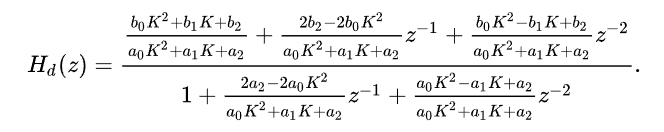
• 즉 고정된 파라미터가 필요한 상황이라면 위의 조건을 따라서 계산을 하면 정확하겠지만 실시간의 파라미터 변화를 추적하기 위해서는 연산자체의한계가 존재하기 때문에 간략한 방법을 쓰기도 함. 해당 방법은 각 필터 설계를 진행하면서 설명

출처 : https://en.wikipedia.org/wiki/Infinite_impulse_response