Faster R-CNN

Mechboy·2025년 1월 18일

논문 분석

목록 보기

4/5

Deep Residual Learning for Image Recognition 논문정리

1. introduction

1.1 도입 배경

기존 2 stage object detection에서는 바운딩 박스를 지정하는데 많은 자원이 필요하여 계산속도가 느려지는 병목현상이 문제가 됨
RPN은 기존에 추출된 feature map을 통해서 연산을 하기 때문에 추가 연산을 필요하지 않은 장점이 있음
더나아가 신경망으로 모든 모델이 구현되어 학습이 용이하여 시스템 최적화에 대한 이점이 있음

2. Faster R-CNN

2.1 Faster R-CNN의 구조

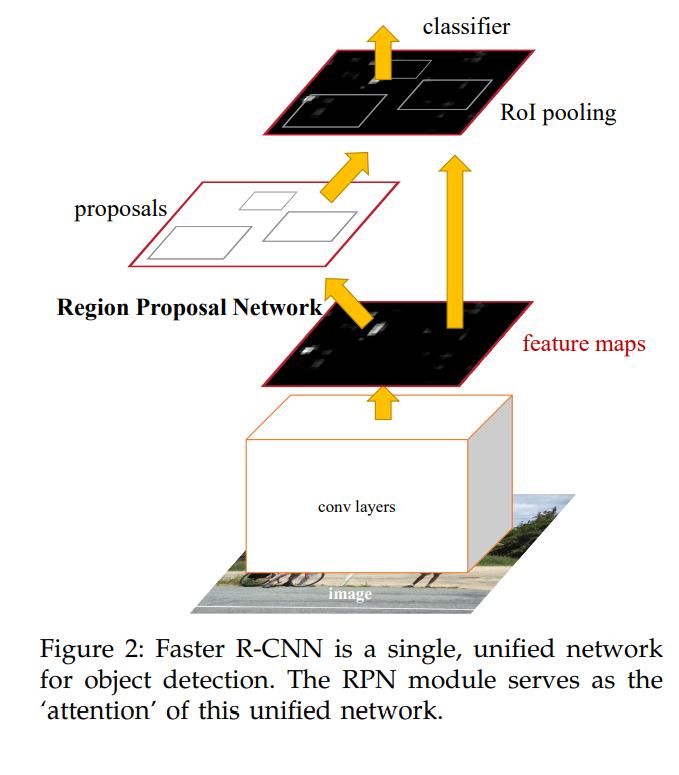
Faster R-CNN은 크게 2가지 영역으로 구분이 된다.

추출된 Feature Maps 를 기준으로 주목해야 되는 ROI를 제안 해주는 'Region Proposal Network'
해당 ROI를 기준으로 사물을 분류 하는 classifier로 나누어져 있음

2.2 RPN layer

RPN layer 기본적으로 사물의 유무를 판단하는 Regression layer와 사물이 있는 좌표를 출력함
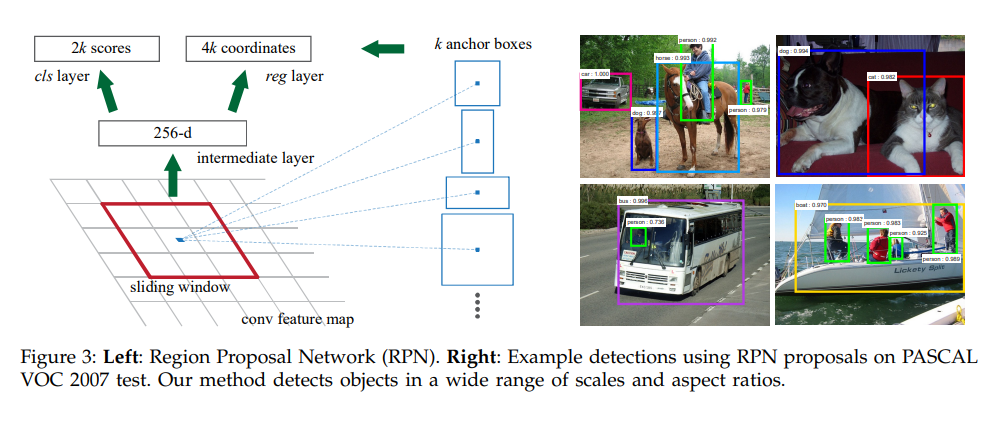
RPN의 입력으로는 CNN-layer를 통해 원본이미지에서 추출한 convolutional feature map을 사용함. 각 레이어는 sliding window 기법으로 스캔하여 영역제안에 필요한 데이터를 입력을 받음. 이떄 사용하는 슬라이딩 윈도우의 사이즈 (n*n)은 최종 feature map의 크기에 따라 결정이됨.
그리고 최종적으로 regression layer와 classification 레이어로 나뉘어서 결과값이 전달이 됨.

2.3 Anchors

앵커는 레퍼런스 박스의 중간지점의 좌표를 의미함.
앵커는 특정 크기와 종횡비를 가지게 되며 해당 논문에서는 k=9를 기준으로 설정
각 슬라이딩 윈도 위치에서 여러개의 영역을 제안할 수 있음. 각 위치에서 만들 수 있는 제안의 최대 개수는 k로 가정
reg layer는 k의 박스좌표를 인코딩 하는 4k개 출력, 각 포인트에서 출력은 시작점(x1,y1), 끝점(x2,y2)로 총4개를 가짐
cls layer는 k의 박스좌표를 인코딩 하는 2k개 출력, 각 포인트에서 출력은 사물이 있을 확률과, 없을 확률로 구분이 됨

2.4 Translation-Invariant Anchors

앵커를 기준으로 영역을 계산하는 함수도 위치 이동(Translation)에 대한 불변성을 갖는게 특징임
앵커를 사용하게 되면 k=9 일 경우에 (4+2)*9 차원의 컨불루션 레이어만 사용하여 학습이 가능함 -> 즉 컨볼루션의 feature map의 채널에 따라 채널수만 변경이 되는것이지, 절대적인 채널 수가 많은것이 아니라 모델이 가벼운 장점이 있음

2.5 Multi-Scale Anchors as Regression References

앵커 기반 설계는 기존 2가지 방법 feature pyramids, sliding window 방식 보다 효율 적임.
여러 스케일의 박스 앵커를 기준으로 바운딩 박스를 사용하여 단일 스케일의 특징맵만 사용할 수 있어 연산시간의 이점을 가지게 됨.

2.6 loss function of RPN

RPN은 각 앵커에 대해 두 가지 연산을 함
- 이진 분류(Classification): 주어진 앵커가 객체를 포함하고 있는지 아닌지 판단
- 바운딩 박스 회귀(Bounding box regression): 객체를 포함하고 있는 앵커라면 앵커의 위치와 크기가 실제 객체 맞게 조절
이를 활용하여 RPN은 multi-task 손실함수를 사용 함
1. 분류손실
- 각 앵커에 대해서 객체 유무를 판단하는 이진 분류 문제, 교차 엔트로피 손실을 사용해서 계산
1. 회귀 손실
- 객체가 있다고 예측된 앵커에 대해, 실제 개체의 경계 박스와 얼마나 차이가 있는지를 측정하는 회귀 문제에 데한 손실, 보통 Smooth L1 loss function을 사용하여 계산함
각 손실을 계산하면 아래와같이 계산이됨 $L({p_i},{t_i}) = \frac{1}{N_{ds}}\sum_i L_{ds}({{p_i}{p_i^*}}) + \lambda\frac{1}{N_{reg}}\sum_i p_i^*L_{reg}({{t_i}{t_i^*}})$

i는 앵커의 인덱스를 의미

$p_i$ 는 객체일 확률을 의미하고, $p_i^*$ 는 실제 레이블의 여부

$p_i^* = 1$ 일때만 바운딩 박스 loss fucntion을 계산함, 즉 배경이라고 판단되면 바운딩 박스를 생성하지 않음

$t_i$ 는 예측된 바운딩 박스 값이고 , $t_i^*$ 는 실제 바운딩 박스 값임

$L_{ds}$ 와 $L_{reg}$ 는 각각의 classification, regression의 로스 함수를의미

$\lambda$ 는 각각의 classification, regression의 로스 함수의 균형을 맞춰주는 하이퍼 파라미터임, 한쪽이 일방적으로 크거나 작은것을 방지함

$N_{ds}$ 와 $N_{reg}$ 는 각각의 classification, regression의 정규화 상수를 의미