Image sementation

이미지 프로세싱에서는 대표적으로 2가지 방법으로 필터링을 진행함

-. Spatial filtering : 커널 행렬을 이용하여 특정 지점의 이미지 행렬의 원소값을 바꾸는 방법
-. Intensity Transformations : 행렬의 한 원소지점을 변환 하는 방법

이 글에서는 우선적으로 contrast stretching이라고 하는 단일 원소의 픽셀 값 변환에 대해서 먼저 이야기 해볼 예정이다. contrast stretching을 사용하는 이유는 Enhancement라고 불리는 기본적인 이미지 처리방식을 하기 위해서임.

출처 : https://www.mathworks.com/discovery/image-enhancement.html

위 그림과 같이 쌀알과 배경의 구분을 명확하게 하여 쌀의 형상의 검출을 쉽게 한다거나 하는 방식으로 원본이미지를 의도적으로 처리하여 컴퓨터비전에서 쉽게 처리하거나 시각적으로 보기 좋은 이미지로 수정하는 방법임

1. contrast stretching
   이미지 매트릭스에서 이웃 픽셀의 값을 고려하지 않고 단일 픽셀만 변환 할 때 사용함

s= T(r)

함수 T는 픽셀변환 함수로 r은 원본 이미지 매트릭스의 원소 I_ij를 이미지 매트릭스 S로 매핑을 시켜주는 함수로 보면 된다.

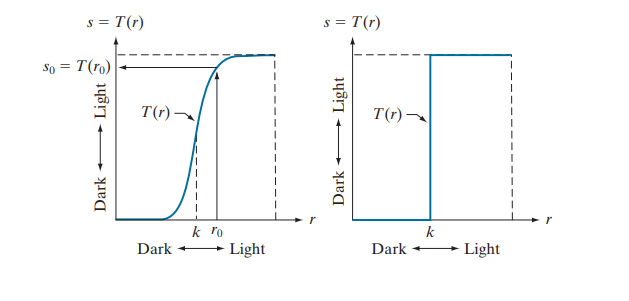
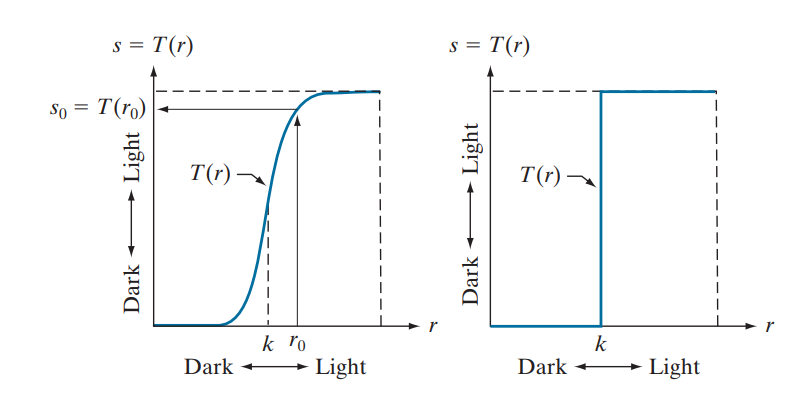
이때 k 기준점을 중심으로 하여 밝기 변환을 의미함

본격적인 이미지 프로세싱에 앞서 샘플 이미지 생성

#이미지 생성
import cv2
import numpy as np
import plotly.express as px

image = cv2.imread("Image_Processing_tutorial.jpg",cv2.IMREAD_GRAYSCALE )
image_matrix = np.array(image)
Original_image= image_matrix

fig = px.imshow(image_matrix,color_continuous_scale=px.colors.sequential.gray)
fig.show()

2. 대표적인 contrast enhancement 함수

Negative fixel

s = T(r) = L - 1 - r

Python으로 구현 하면 아래와 같이 표현이 가능함
(Jypyter notebook을 활용하여 위쪽 소스코드의 변수를 계속 사용중)

def Negatvie_fixel(size,r):
    s = 2**size - 1 - r
    return s

X, Y = image_matrix.shape
NEGATIVE_IMAGE = np.zeros((X,Y))

for i in range(X):
    for j in range(Y):
        NEGATIVE_IMAGE[i,j] = Negatvie_fixel(8,image_matrix[i,j])

fig = px.imshow(NEGATIVE_IMAGE,color_continuous_scale=px.colors.sequential.gray)
fig.show()

위와 같이 밝기 정보를 바꾸어 준다. 일반적으로 이미지픽셀 밝기 분포가 어두운쪽이 많을때 쓰면 좋다. 반대로 밝은 픽셀의 분포가 많다면 저렇게 되니 조심

2. Sigmoid function

$T(r) = (L-1) * \frac{1}{1 + e^{-a(x+k)}}$
라는 수식으로 표현 가능함
a는 시그모이드 함수의 기울기를 결정하고 k는 기준점으로 나타내고 $L-1$는 픽셀 발기 범위를 표현함

def Sigmoid(size,A,K,R):
    result = (2**size - 1) * ((1/(1+np.exp(-A*(R-K)))))
    return int(result)

Z = []

for i in range(256):
    Z.append(Sigmoid(8,0.5,150,i))

fig = px.line(x=list(range(256)), y=Z, title='Sigmoid function')
fig.show()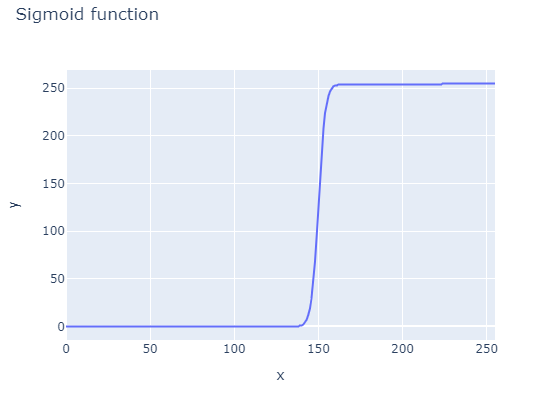

이 함수를 이미지에 적용시켜보면

def Sigmoid(size,A,K,R):
    result = (2**size - 1) * ((1/(1+np.exp(-A*(R-K)))))
    return int(result)

X, Y = image_matrix.shape
Sigmoid_TEST = np.zeros((X,Y))

for i in range(X):
    for j in range(Y):
        Sigmoid_TEST[i,j] = Sigmoid(8,0.5,150,image_matrix[i,j])

fig = px.imshow(Sigmoid_TEST,color_continuous_scale=px.colors.sequential.gray)
fig.show()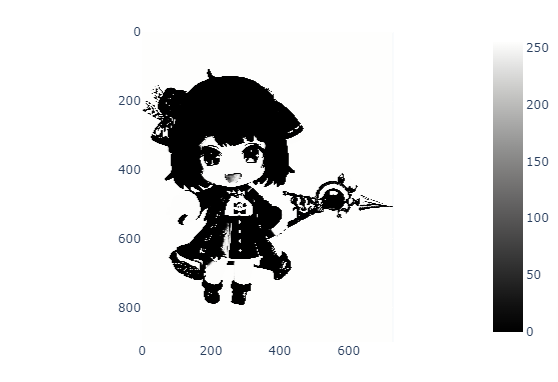

위와 같이 나온다 일반적으로 우리가 흔히 사진으로 찍는 이미지에서는 활용도가 떨어지고 기하학적으로 구분이 명확한 이미지에서 효과가 좋음. 아래 이미지는 IC칩의 단면도 인데 여기서 웨이퍼의 실리콘과 금속선을 구분을 명확하게 하기 위해 Sigmoid function을 사용하여 금속선을 좀 더 명확하게 볼 수 있도록 이미지 전처리가 가능함.

이미지 출처 : https://www.cl.cam.ac.uk/~djg11/socdam-patterns-hls-touchstones/soc-design-patterns/sp2-power/zhp416c1cc9d.html

<적용전>

<적용후>

일단 이외에도 다양한 방법 LOG 함수 혹은 exponential와 같은 방법이 있지만 이방법에 대해서는 추가적으로 작성할 예정