convolution

• convolution은 합성곱이라는 의미에서 시스템 분석에서 많이 활용 하는 기법
• 컨벌루션을 이해하기 위해서는 우선 LTI(linear time invarient) 와 impulse 함수에 대한 응답을 알아야 함

Impulse function

• 임펄스 함수의 정의는 적분을 했을때 값이 1로 표시 되는 함수이다.

${\delta}(t) = \int_{-\infty}^t \delta(\tau) \, d\tau$

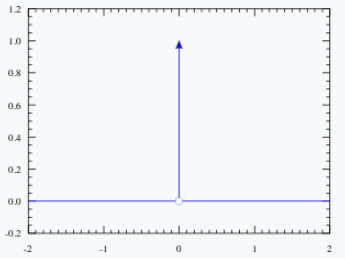
impulse 함수의 대표적인 성질

1. $t$가 0이 아닐때는 ${\delta}(t) = 0$
2. $t$가 0인 경우에는 ${\delta}(t) = \infty$
3. $1 = \int_{-\epsilon}^\epsilon \delta(t) \, dt$ 입실론의 크기와 관계 없이 성립
4. impulse 함수는 even funtion

• impulse 함수의 경우 시스템의 전달함수를 구할때 사용함

LTI

• Linear time invarient system은 신호 및 시스템을 구성하는데 매우 중요한 개념이다.
• 시스템은 입력과 출력이 시간에 독립적이고
• 입력이 선형이면 출력도 선형이라는 의미가 있음
• 수식으로 표현하면 다음과 같다.

LTI 시스템의 특징

1. 선형성
   $f(x+y) \rightarrow F(x) + F(y)$
   $f(a*x) \rightarrow aF(x)$
2. 시불변성
   $f(x+t_0) + g(x+t_0) \rightarrow F(x+t_0) + G(x+t_0)$

convolution

• convolution은 시간,공간 영역에서 입력함수와 전달함수의 관계를 나타 내주는 식으로 특정 시스템에 입력을 넣으면 나오는 출력을 연산해주는 연산자임

1. 연속시간에서의 컨볼루션 연산

$F(t) = \int_{-\infty}^{\infty} f(\tau) \cdot h(t-\tau) \, d\tau$

2. 이산시간에서의 컨볼루션 연산
   ${F}(x) = \sum_{i=0}^{k-1} \text{h}(i) \cdot \text{f}(x+i)$

• 여기서 입력을 임펄스 함수로 넣어주면 아래와 같은 출력으로 나타낼 수 있음
• 입력함수로 임펄스 함수를 활용하면 시스템의 전달 함수를 바로 확인 할 수 있는 강점이 있음

1. 연속시간에서의 컨볼루션 연산

$h(t) = \int_{-\infty}^{\infty} \delta(\tau) \cdot h(t-\tau) \, d\tau$

2. 이산시간에서의 컨볼루션 연산
   ${h}(x) = \sum_{i=0}^{k-1} \text{h}(i) \cdot \delta(x+i)$

이미지 영역에서 convolution

• 이미지 영역에서 convolution은 x,y좌표를 2차원계를 기초로 하여 진행함
• x 공간에 대한 convoution 연산 1번, y공간에 대한 convolution 연산 1번 총 2번이 수행 되어야 함

1. 이미지 공간에서의 convolution
   ${Output}(x, y) = \sum_{i=0}^{h-1} \sum_{j=0}^{w-1} \text{Input}(x+i, y+j) \times \text{Kernel}(i, j)$