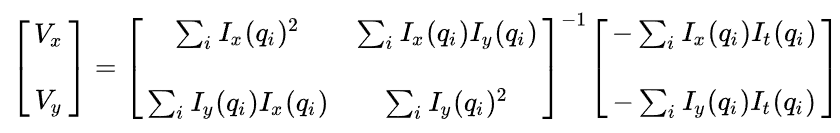옵티컬 플로우 (Optical Flow)

1. 서론

1.1 옵티컬 플로우의 정의와 활용

• optical flow는 관찰자와 배경간의 상대적인 움직임으로 인해 나타나는 패턴 변화를 추적하는 방법중 하나임.
• 주로 영상압축이나 모션 추적에 대해서 활용함

2. 이론적 배경

2.1 움직임과 밝기 불변 가정(Brightness Constancy)

• 밝기 불변 법칙은 어떤 물체가 한프레임에서 다른 프레임으로 이동하더라도, 물체의 밝기값이 변하지 않는 다는 가정임
• 즉 관찰자의 시선이 고정이 되어있다면 물체의 위치만 평행이 이동을 하는것이지 밝기가 변하지 않는다고 가정
• 수식으로 표현하면 아래와 같이 표현가능
  $I(x,y,t) = I(x+u,y+v,t+1)$

3. Lucas Kanade 알고리즘

3.1 Brightness Constancy 의 문제점

• 한개에 수식에 표현된 optical flow에 대한 식을 보면 변수가 $u, v$ 2개 있는 문제가 있음
• 해당 식에서 고유한 $u, v$를 찾기 위해서는 추가 제약이 필요하게 됨.

3.2 Lucas Kanade 제약 조건

• Lucas Kanade는 임의의 영역 $(n,n)$ 공간에서의 모든 픽셀의 방향이 일정하다고 가정
• 즉 해당 윈도우에서 u,v가 전부 동일하다고 가정하고 윈도우 영역내의 n*n의 좌표에 대한 식을 연립으로 세워 u,v를 구한다.
  $I(x_1,y_1,t) = I(x_1+u,y_1+v,t+1)\\ I(x_2,y_2,t) = I(x_2+u,y_2+v,t+1)\\ \cdots$

4. Lucas Kanade 계산

4.1 기본적인 IDEA

• 기본적으로는 옵티컬 플로우는 E(v) 목표함수에서 가장 작은 벡터 V를 찾는 함수를 찾는 과정을 의미함
  $E(v) = \|A\,v - b\|_2^2 \;=\; (A\,v - b)^{T}(A\,v - b)$
• 여기서 $E(v)$ 에대해서 그래래디언트 연산을 해서 0이 되는값을 찾으면 자연스럽게 E(v)구간에서 가장 작은 값을 가지는 구간을 얻게 될 것으로 아래 식을 계산하는것이 방법

4.2 $\nabla_E(v) =0$ 계산

• 여기서 A,b에서 각 구간의 포인트가 n가 있다고 가정하면 A,b 행렬은 아래와같이 표현이 가능함

  $A = \begin{bmatrix} I_x\bigl(q_1\bigr) & I_y\bigl(q_1\bigr) \\ I_x\bigl(q_2\bigr) & I_y\bigl(q_2\bigr) \\ \vdots & \vdots \\ I_x\bigl(q_n\bigr) & I_y\bigl(q_n\bigr) \end{bmatrix} ,\quad b = \begin{bmatrix} -\,I_t\bigl(q_1\bigr) \\ -\,I_t\bigl(q_2\bigr) \\ \vdots \\ -\,I_t\bigl(q_n\bigr) \end{bmatrix}$

• $\nabla_{v}E = 2\,A^{T}(A\,v - b) \;=\; 0$ 식에 맞게 식을 유도하면 아래와 같이 최종식을 구할 수 있음
  $A^{T}Av \;=\; A^{T}b$
  $v \;=\; (A^{T}A)^{-1}A^{T}b$

• 즉 $v \;=\; (A^{T}A)^{-1}A^{T}b$ 를 계산하면 최종값을 얻을 수 있고 계산식을 일반화 하면 아래와 같음
  

5. 출처

• https://en.wikipedia.org/wiki/Lucas%E2%80%93Kanade_method
  -https://en.wikipedia.org/wiki/Optical_flow