Gaussian Mixture Model(GMM)

*본 포스팅은 서울대학교 데이터사이언스 대학원 이상학 교수님의 "데이터사이언스를 위한 머신러닝과 딥러닝2" 강의록을 기반으로 함.

• Clustering에는 많은 방법들이 있다.
• Clustering 방법들에 대한 평가를 위해서, 어떠한 측도가 필요할 것이다.
• 이를 위한 하나의 접근법은, Data가 특정 생성모델에 의해 generated 되었다고 보는 것이다. 즉 특정 모델을 가정하고, 통계학에서의 MLE와 비슷한 방법론을 이용하여 파라미터를 추정한다.

• Gaussian Mixture Model의 pdf는 단순히 정규분포의 가중합이다.
• Gaussian의 선형 결합은 거의 모든 smooth density를 근사할 수 있다고 한다.
  - 이에 대한 직관적인 설명을 stack exchange에서 찾았다.
  
  아주아주 간단히 요약하면, 임의의 pdf는 direc-delta함수의 선형결합으로 표현되고, gaussian distribution은 분산을 0으로 보내면 direc-delta로 수렴하므로 gaussian의 mixture를 통해서 any pdf를 근사할 수 있다는 논리다. 이것만 보면 꼭 임의의 pdf를 근사하기 위해 gaussian의 mixture를 쓸 필요는 없어보인다.

• GMM을 fitting 할 때의 기본적인 접근법은, Maximum Likelihood Estimator를 찾는 것이다.
• 이 때 두 가지 문제가 발생한다.
  - Singularities : 만약 mixture model 내에 한 component가 단 하나의 데이터셋에 대응된다면, 해당 component에 해당되는 likelihood가 무한대로 발산하게 된다(해당 component는 direc-delta로 수렴하게 된다) 또한, 해당하는 원소의 분산이 0으로 수렴하므로, X의 공분산행렬은 singular하게 된다. (해당 원소가 대응되는 row/column의 원소가 모두 0으로 수렴) 공분산 행렬의 Inverse는 MLE를 산출하는데 필요한데, 이를 구하기 어렵게 된다.
  - Identifiability : GMM은 Gaussian의 단순 가중합이므로, parameter의 순서에 상관이 없이 같은 모델에 대응될 수 있다.
• 결론적으로, 일반적인 미분 방법을 이용하여 GMM을 fitting하는 것은 무리가 있다.

• Naive 한 ML방식 대신, GMM을 Fitting 할 때는 각 Data point x가 어떠한 Gaussian component에서 왔는지를 나타내는 Latent variable Z를 도입하여 문제를 단순화한다.

• 이러한 잠재변수의 도입이 어떻게 기존 ML방식의 문제점을 해소시키는가?
  - 이는 Latent Variable하에서의 optimization 방식인 EM 알고리즘을 설명 한 후 다시 언급하도록 하자.

• Hidden latent variable Z를 도입하여 기존의 log-likelihood를 다시 표현했다.
• sum-inside-log의 상황은 다음과 같은 이유로 최적화가 어렵다.
  - 여기서 u와 $\Sigma$는 벡터다. log 안에 sum이 있으면, log는 비선형 함수이므로 component별로 분리가 매우 어렵고, 즉 각 component 간의 상호작용을 모두 고려한 최적화가 이루어져야 한다. 즉 문제가 복잡해진다.
  • 비슷한 맥락에서, 해가 closed-form으로 나오지 않는다.
    
  • 이 함수의 최적화를 위해 Gradient Descent를 쓰지 않는 이유도 이에 대응될 것이다.

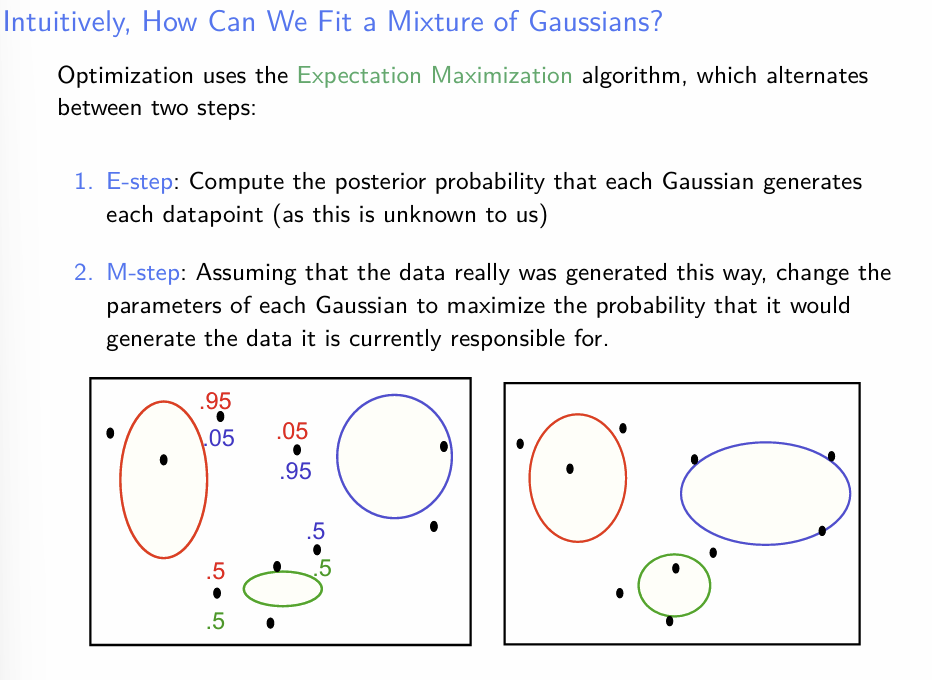
• 직관적인 EM에 대한 설명이다.
  - observed data 를 기반으로 한 complete data(X,Z)의 가능도를 계산한다
  - 위의 가능도를 최대화시키는 방향으로 parameter를 update 시킨다.

• 다시 말하면, E-step에서는 observed data를 조건부로 하여 latent variable의 posterior를 산출한다.
  - 이 때, 각 data point에 대하여 z의 값이 확률적으로 부여되므로, 하나의 데이터 포인트가 하나의 가우시안 컴포넌트에 과도하게 맞춰지는 문제를 해결 할 수 있다.
• M-step에서는 posterior를 최대화시키는 방향으로 parameter-update를 진행한다.
  

• E step을 조금만 더 자세히 살펴보자.
  앞서 언급되었던 E-step에서의 posterior은 Bayes Theorem을 이용하여 간단하게 계산이 가능하다.

• M-step에서는 앞서 구했던 $\gamma$를 이용하면 sum-inside-log 상황을 탈피할 수 있다.
• 위의 EM step 을 반복한다.

• 요약하면 전체적인 흐름은 다음과 같다.
• E-step에서는 given data에 대한 Latent Variable에 대한 조건부 분포를 구하고, 이를 이용해서 계속해서 parameter를 update시킨다.