Hidden Markov Models(HMM)

*본 포스팅은 서울대학교 데이터사이언스 대학원 이상학 교수님의 "데이터사이언스를 위한 머신러닝과 딥러닝2" 강의록을 기반으로 함.

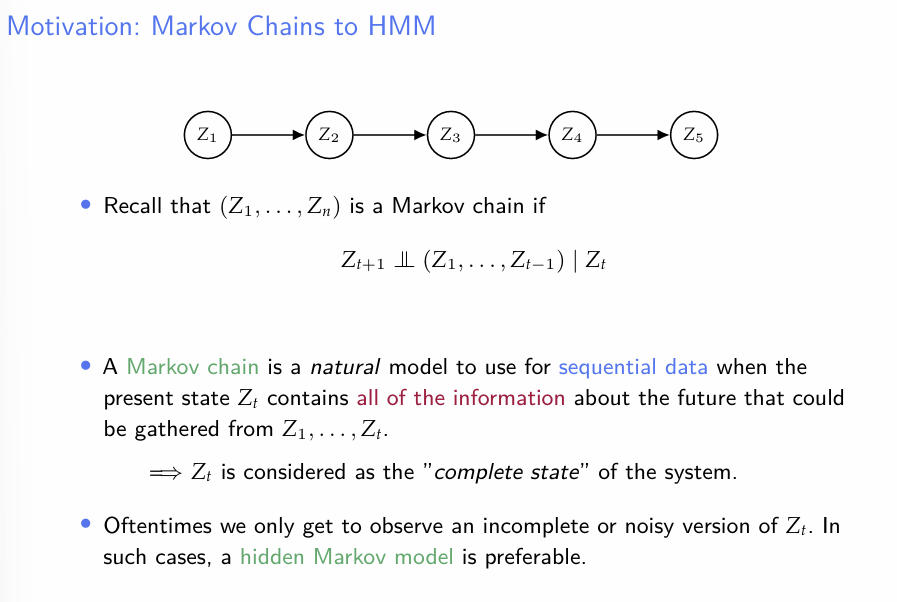
• 기존의 markov chain의 가정에 의하면, 모든 상태는 그 직전 상태에만 의존하므로, 이전 상태에 현 상태에 대한 모든 정보가 포함된다고 생각되는 경우에 한하여 사용될 것이다.

• 만약 우리가 현 상태에 대한 불완전한 정보나 missing이 포함된 데이터만 관찰 할 수 있다면, Hidden Markov Model은 적절한 선택지일 것이다.

• 여기서 Z는 Hidden state, X는 Outcome state를 의미이며, 우리는 X를 현재 관찰하고 있다.
• 예를 들면, 우리가 과거 날씨에 관한 정보를 잘 알지 못하는 상황이라고 가정하면 Z는 weather, X는 그 날에 했던 activity라고 둘 수 있다.

• HMMs는 다양한 sequential data에 대하여 효과적인 모델이라고 한다.
• HMM에 관한 inference와 그에 대한 알고리즘 세 개를 소개한다.
  - Viterbi : Z의 Value가 관심대상이다. 즉, $argmaxP(Z|X)$를 알고자 한다.
  - Forward-Backward : State에 대한 확률계산을 위한 알고리즘이다.
  - Baum-Welch : Parameter 추정에 관한 알고리즘이다.
  

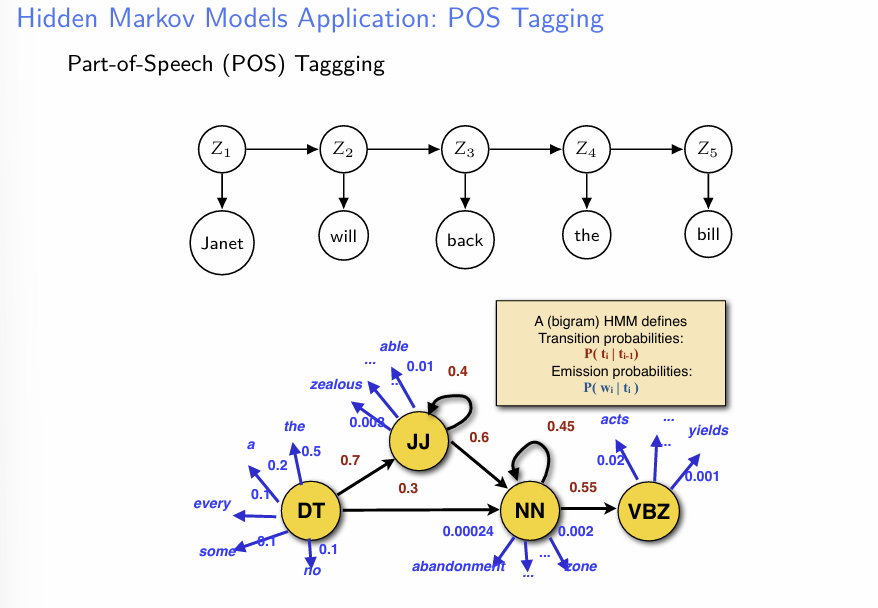
• Markov Chain의 활용 예시를 소개한다. POS는 NLP문제에서 단어의 품사를 예측하는 방법론이다.
  - 자료와 같이, 품사 Z를 Hidden State로 생각하고, 우리는 현재 실제 문장 X를 관측하는 상황이라고 가정한다.

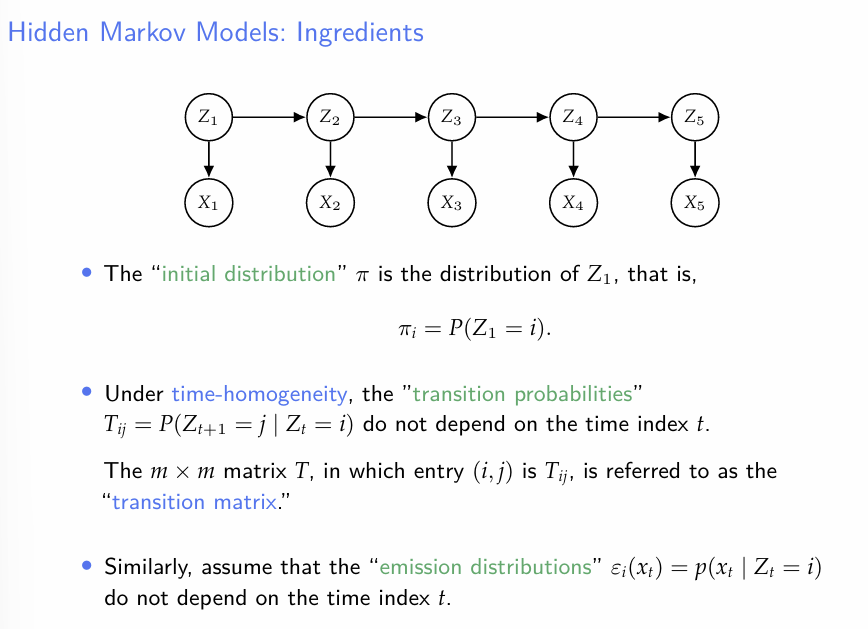
• HMM의 기본 셋팅에 대하여 설명한다.
• Hidden State Z의 전이확률은 시간 t에 관련 없이 동일하다(우리가 지금까지 다룬 Markov Chain은 이를 가정하고 있다. 물론 당연히 Markov Chain이 이 조건을 만족할 필요는 없다)
• $X_i$의 $Z_i$에 대한 조건부분포는 시간 t에 관계가 없다.

• 위의 셋팅에 따라서 HMM을 정의했다고 생각하면, 이제 우리에게 남은 과제는 일단 위의 세개가 있다.

• $\arg \max_z P(Z|X)$ 를 찾기 : viterbi 알고리즘은 이를 해결하는 방법 중 하나다.

• $P(X)$ 찾기 : ex) Forward-Backward 알고리즘

• $\arg\max_\theta P(x:\theta)$ 찾기 : ex) baum-welch

• 이 때, $\theta$는 $<\pi, T, \epsilon>$를 포함한다.

  • $\pi$는 초기상태를 의미한다.
  • T는 Z의 전이행렬을 의미한다

Viterbi Algorithm

• 먼저, viterbi 알고리즘에 대하여 설명하자.
• 알고리즘의 목적은 $P(Z|X)$를 최대화시키는 Z를 찾는 것이다.
• 만약 이 문제에 대하여 Naive하게 접근한다면, 확률계산을 $n * m^n$번 만큼 해야한다.
  • $nm^n$이라는 숫자가 나온 이유는 다음과 같다. 일단 z의 모든 조합은 $m^n$개이다. 또한, 각 z에 대한 조건부확률을 계산하는 것은 아래의 공식 때문에 최대 n번 필요하다.
    
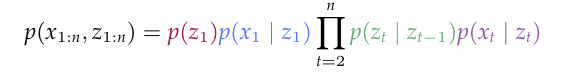
  • 즉 naive한 접근으로의 order는 $n*m^n$이 된다
• 이러한 복잡도를 줄이기 위해 Viterbi 알고리즘이 사용된다.
  

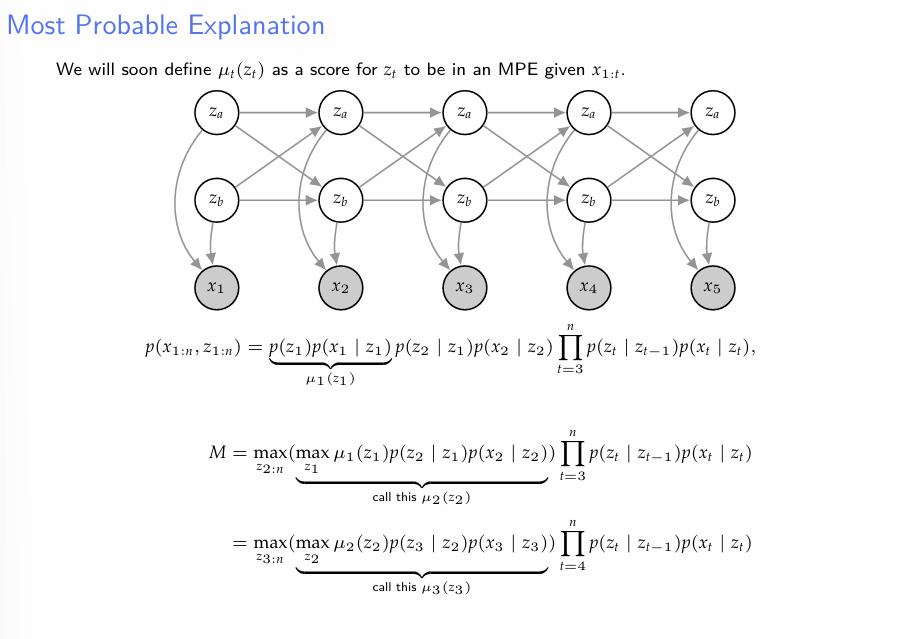
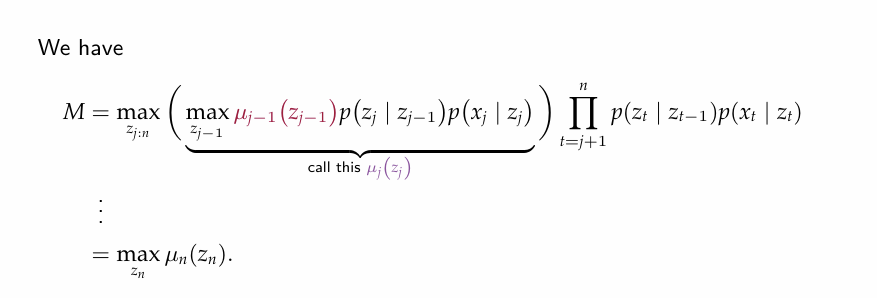
• Viterbi Algorithm의 기본적인 아이디어는 다음과 같다.
• Naive한 접근을 할 때, 우리는 모든 z1..zn의 조합 총 $m*n^m$ 개의 조합에 대하여 모두 확률을 계산하게 된다.
• 하지만, 흥미있는 대상이 확률의 Maximum일 때는, 굳이 모든 상태공간을 다 찾아 뒤질 필요가 없다.
• 예를들어, $Z_1 \rightarrow Z_4$ 까지의 경로 중 X에 대하여 가장 높은 조건부확률을 가지는 경로를 조사하기 위해선, Z가 2개의 state를 가질 수 있다는 상황 하에서 naive한 방법론으로는 $2^4 = 16$개의 Route를 비교해야 한다.
• 하지만 만약 우리가 현재 최대확률을 가지는 $Z_1 \rightarrow Z_3(A)$, $Z_1 \rightarrow Z_3(B)$ (여기서 A,B는 Z의 state. 즉 $Z_1 \rightarrow Z_3(A)$는 $Z_3$이 A로 끝나는 경로를 의미한다.) 를 알고 있다면, 우리는 최대확률을 가지는 $Z_1 \rightarrow Z_4(A)$ 를 찾기 위해 2개의 경로만 비교하면 된다. $Z_1 \rightarrow Z_4(B)$의 경우에도 마찬가지다.

• 결론적으로 위의 아이디어를 체계화하면 다음과 같은 알고리즘을 생각 할 수 있다.

• $\mu_j(z_j)$는 t = j-1에서 각 상태로의 최적 경로에서, 주어진 상태 $z_j$로 가는 경로의 확률이다.

• 이를 연쇄적으로 반복한 후, $M = \max_{z_n}\mu_n(z_n)$을 구하면, 시간 1부터 n까지의 최적의 경로를 찾을 수 있다.

• viterbi 알고리즘의 시간복잡도는, $O(n*m^2)$이다. 기본 아이디어를 생각해보면 이해가 될 것이다.

• Viterbi 알고리즘의 문제점은, 서로 다른 확률들을 연쇄적으로 곱하다보니 결과값이 수치적으로 0이 될 가능성이 존재한다.
• 간단한 해결책은 log를 통해서 확률들의 곱을 log들의 합으로 만드는 것이다.

Forward-Backward Algorithm

• 다음으로 Forward-Backward 알고리즘에 대하여 알아보자. 앞서 언급한대로, 이 알고리즘의 목적은 확률의 계산. 즉 observed X에 대한 Z의 다양한 조건부확률을 계산하는 데 있다.

• forward-backward 알고리즘은 그 이름에서 알 수 있듯이, Forwrad, Backward의 두 부분으로 구성된다.
• Forward probability $s_t(i) = P(Z_t = i, x_{1:t})$
• Backward probabilty $r_t(i) = P(x_{t+1:n}|Z_t=i)$
• $s_t(i) * r_t(i) = P(x_{1:n},Z_t=i)$ : 이러한 성질 덕에 다양한 x에 대한 조건부확률을 구하는 데에 쓰일 수 있다.

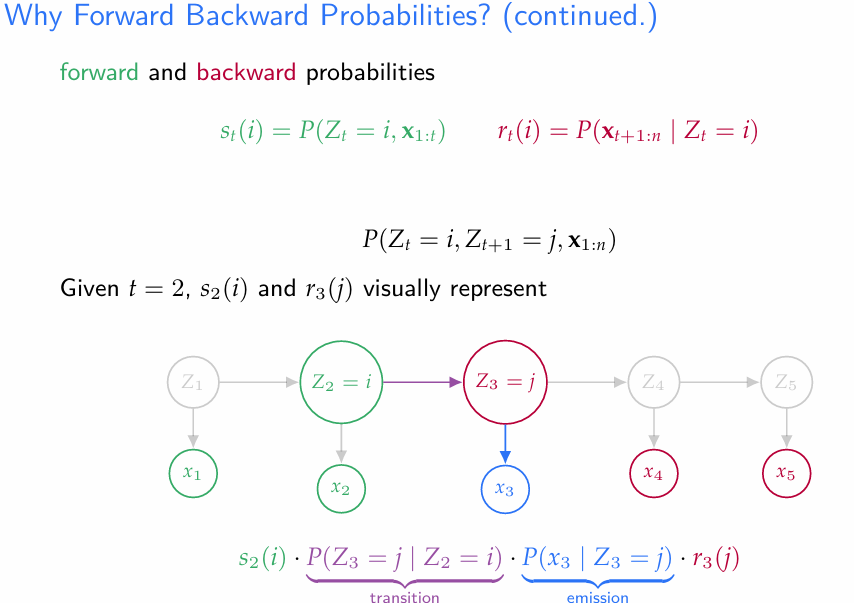
• 이와 같이 forward-backward 알고리즘을 통해 forward, backward probability를 알고 있으면, 적절히 조합하여 원하는 조건부확률을 찾을 수 있다.

• 여기서, Forward probabilty $s_j(z_j)$가 어떻게 정의되었는지 주목하자
• $s_j(z_j) = \sum_{z_{j-1}}s_{j-1}(z_{j-1})p(z_j|z_{j-1})p(x_j|z_j) = \sum_{z_{j-1}}p(z_{j-1}, x_{1:j-1})p(z_j|z_{j-1})p(x_j|z_j) = \sum_{z_{j-1}}p(x_{1:j-1},z_j,z_{j-1})p(x_j|z_j) = \sum_{z_{j-1}}p(x_{1:j},z_j)$

• Backward prob는 위와 같이 계산한다.
  

Baum-Welch algorithm

지금까지의 두 상황은(Z추론, 확률추론) 모두 $\theta = <\pi, T, \epsilon>$을 우리가 알고 있다는 상황하에서 이루어진 것이다. 이제 $\theta$ 자체를 추론하기 위한 Baum-Welch algorithm 을 소개한다.

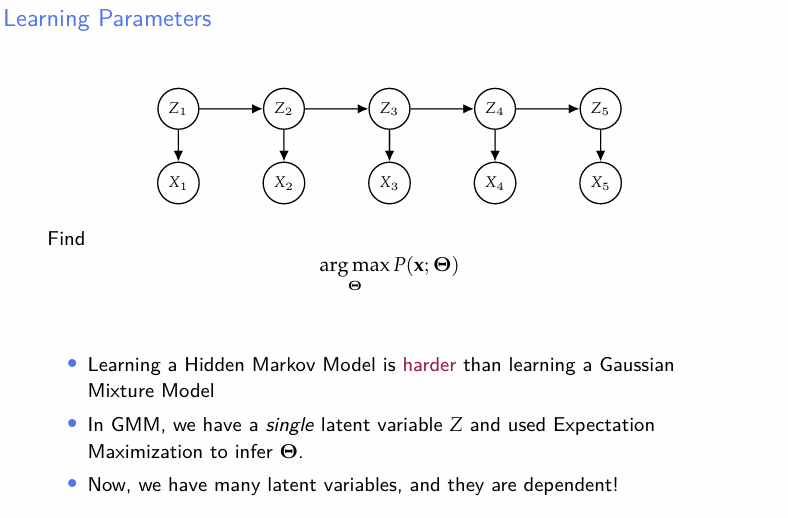
• 일반적으로 HMM에서의 파라미터 추정은 GMM에서에 비해 더 어렵다.

• 잠재변수 Z가 하나가 아니고, 그리고 그들간에 의존성이 있기 때문임.

• Transition probabilty 즉 Z의 전이확률은 위의 그림과 같이 추정할 수 있다. 이는 직관적이기도 하지만, 사실 잘 생각해보면 이산형 Markov Chain에서 어느 상태 i에서 다른 상태로 전이하는 사건은 다항분포를 따르게 되고, 다항분포의 MLE는 그냥 표본비율이 되기 때문에 위와 같이 생각해도 무리가 없다.
• 이를 구하기 위해 우선 $P(Z_t = i, Z_{t+1} = j , x_{1:n})$을 추정해보자.

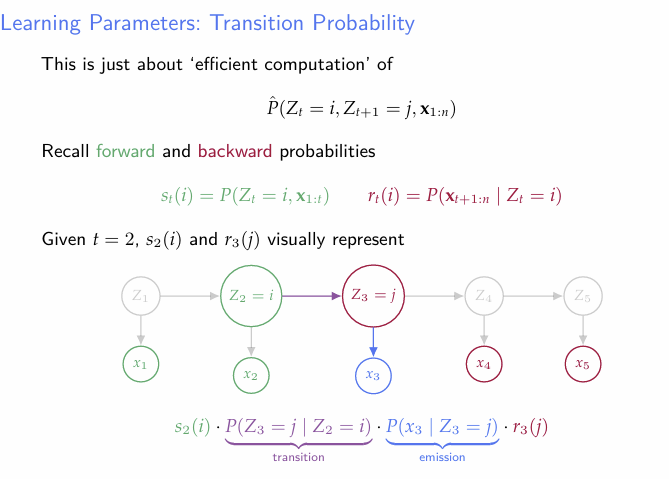
• 예를 들어, Forward Backward를 이용해 $P(Z_2 = i, Z_{3} = j , x_{1:n}) = s_2(i)P(Z_3 = j|Z_2 = i)P(x_3|Z_3 = j)r_3(j)$로 구할 수 있다.