
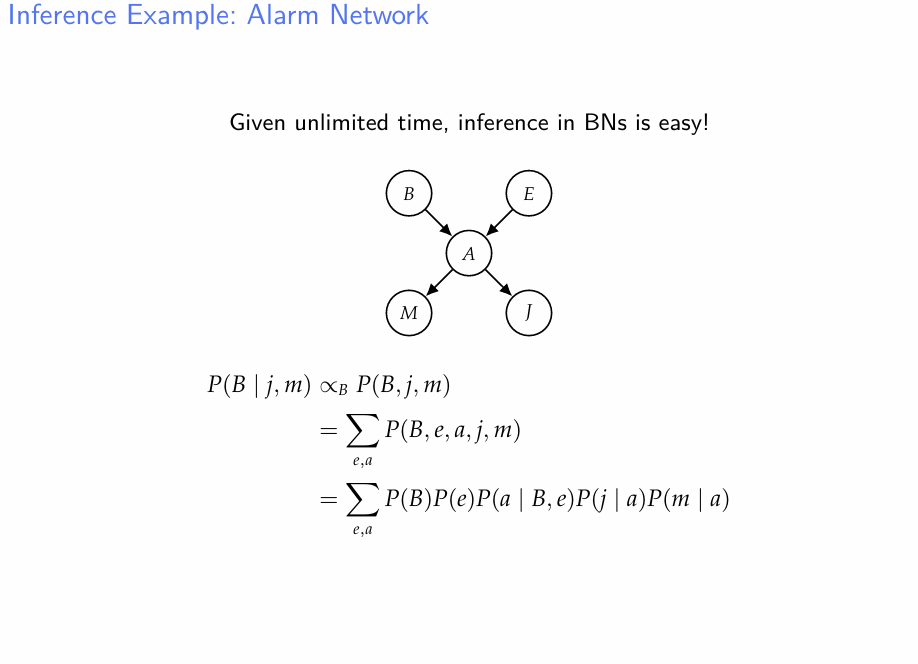
- 베이지안 네트워크에서 값을 모르는 노드를 추론하려면 주로 Bayesian Posterior을 통하여 접근하는 방법을 생각할 수 있다.
-
Markov property를 이용하여 이러한 posterior를 구하는 식을 쓰는 건 매우 간단하다.
-
우리가 사전에 가지고 있는 정보는 Conditional probality table(direct edge간의 조건부분포)임을 다시 한번 상기하자.
-
CPD가 Full로 주어진 상황이 많이 있을지는 생각해봐야겠다. 아마 흔한일은 아닐 것 같다.

-
어쨋든 간에, 시간이 무한대라면, 이러한 inference는 그냥 계산하면 된다.
-
이러한 naive한 접근방식은 의 시간복잡도를 가진다.
- 엣지 수 만큼 곱하는 것을 |e||a| 번 만큼 해야하고, |B|만큼 반복해야 P(B,j,m) 얻을 수 있음
- 더하기는 |e||a||B|번 하면 됨
- 최종 연산량 = (|edge|+1)|e||a||B|
- Hidden variable이 늘어남에 따라서 기하급수적으로 증가한다.
-
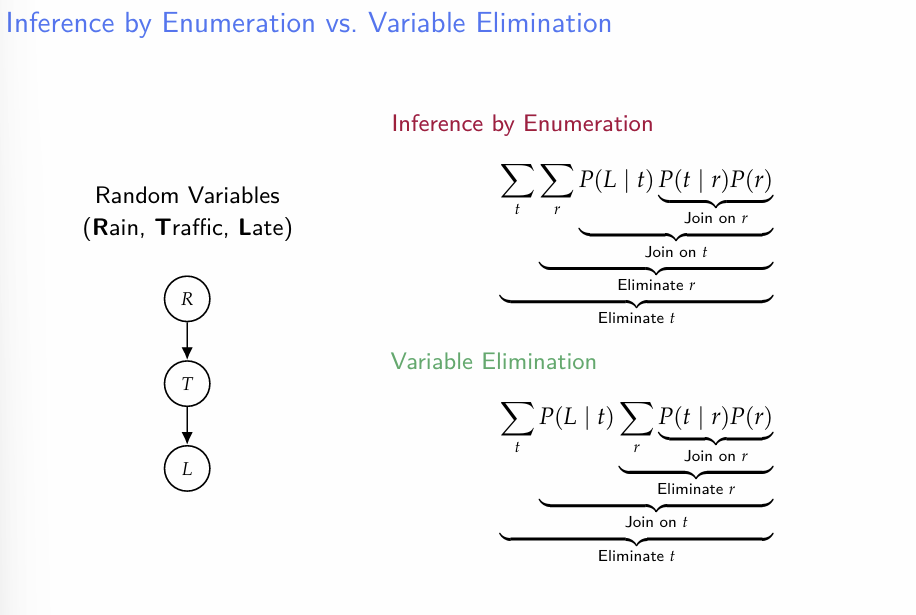
시간복잡도를 줄이기 위해, Variable Elimination이라는 기법을 사용한다.
-
variable elimination은 단순히 sum의 순서를 바꿔서 연산량을 줄이는 기법임.
-
위의 P(L,t,r)을 구하는 두 예제를 생각해보면,
- Enumeration 연산량 : |2||T||R||L| + |T||R||L| = 3|T||R||L|- Variable Elimination 연산량 : (|R|+|R|)|T| + |L|(|T| + |T|) = 2|L|T| + 2|R||T|
-
random L에 대한 확률을 구하려면 결국 L의 원소개수만큼 반복해야하는데, 그 안에 L과 관련이 없는 인자들을 따로 factor로 묶은 다음에 L의 변화에 따른 factor에 대한 연산을 생략하는 technique라고 이해하면 될 것 같다.
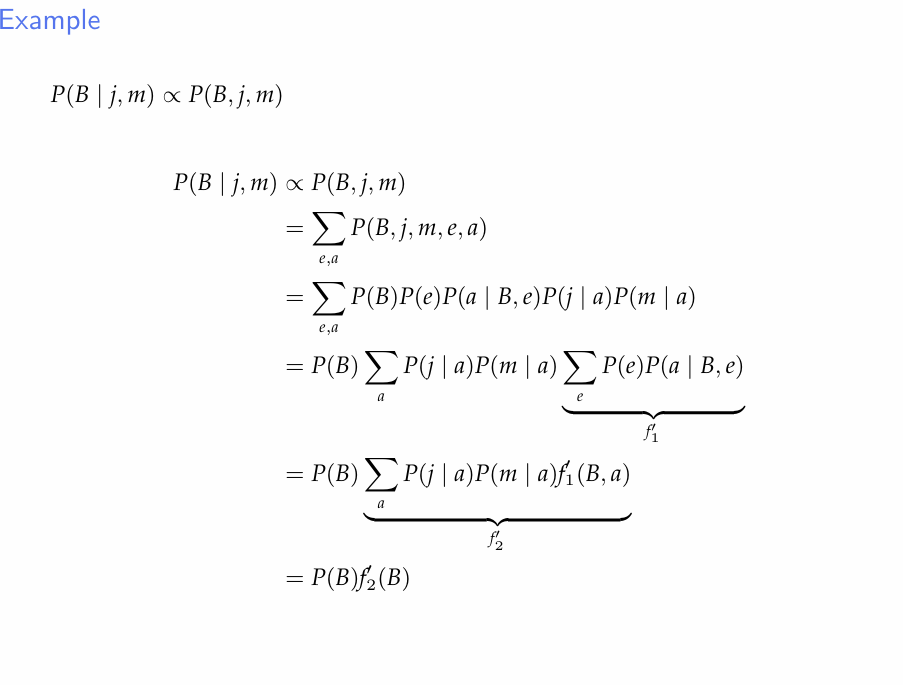
- 아까 나왔던 그래프에 대한 예제를 variable elimination으로 계산하면 다음과 같다.
- sum을 최대한 안쪽으로 넣으면, 일단 곱하기 연산수가 감소한다.
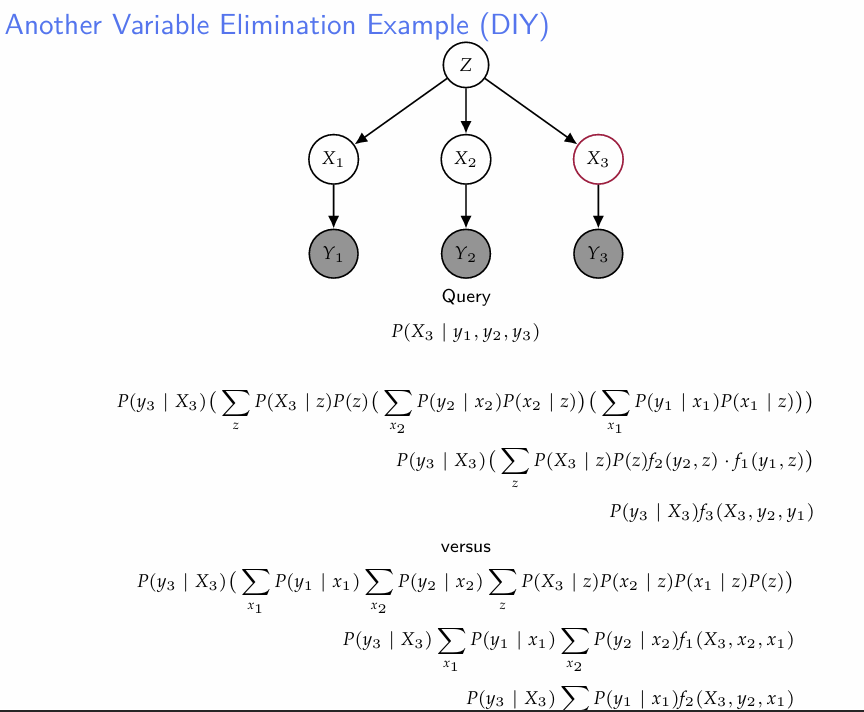
-
하지만 variable elimination하는 방법이 유일한 것은 아니다. 변수 순서를 바꿈에 따라 필요한 계산량이 천차만별이다.
-
그 전에, 왜 이러한 방법에 "variable elimination"이라는 이름이 붙었는지 확인해보자. 사실 sum의 순서를 바꿔서 어느 변수를 소거하는 것은, "소거 변수"를 제외한 나머지 변수들 간의 joint prob을 구하는 것과 같은 연산이다.
-
위의 슬라이드를 보면, 첫번째 방법은 X1, X2, Z 순서대로 변수를 제거하고, 두번째 방법은 Z, X2, X1 순으로 제거한다. Z를 먼저 제거하면, (X1,X2,X3)에 대한 joint를 계산해야 한다. 이 세 변수는 종속적이기 때문에, 직관적으로 보면 연산량이 많아질 위험이 있다.

- 가장 큰 factor의 크기에 의해 연산량이 달라진다고 말하고 있다. 가장 큰 factor의 크기가 작을수록 연산효율이 좋다.
- Factor의 크기 : 각 factor가 가질 수 있는 값의 크기. 즉 factor가 이진변수 n개로 표현되면 크기는 이다.
- 이게 뭔말인고 하니, 결국 위에서 (X1, X2, X3)에 대한 joint를 계산하기 때문에 연산량이 많아진 다는 것과 같은 맥락이다.
- 아까 두 방법 중 첫번째 방법에서는 f1,f2,f3의 크기가 모두 2이다.
- 두번째 방법에서는 f1의 크기가 이 된다.
- 하지만, 어떠한 최악의 경우에는 variable elimination을 무슨 순서로 하든지 exponential 한 연산량에서 더 나아질 수 없다고 한다.

- 지금까지 한 것은 참 값을 구하는 Exact Inference 방법이다.
- 우리는 Exact가 아니라 approximate하게 확률을 추론 할 수도 있다. 정확한 결과 대신 계산 속도와 효율성에 장점이 있다.
