FFT(Fast Fourier Transform)연산을 수행할 때, 화면에 포착된 신호의 앞과 끝이 일치하지 않는 경우가 발생할 수 있다. 이렇게 이어지는 윈도우와 완벽하게 일치하지 않는 불연속에 의해서 발생하는 이슈에 대해서 다루는 것이 window라고 불리는 테크닉이다.
불연속에 의해서 발생하는 이슈를 줄이거나 제거하려고 윈도우를 적용할 때, 윈도우의 종류가 많아서 어떤 윈도우를 적용할 지 결정하는 것이 또다른 이슈가 되곤 한다. 어떤 윈도우를 적용하느냐에 따라 결과의 분해능, 얼마나 높은 주파수의 리키지가 발생하는 지 또는 주파수 성분과 다른 주파수 성분 사이의 왜곡이 발생하는 지의 결과가 달라진다.
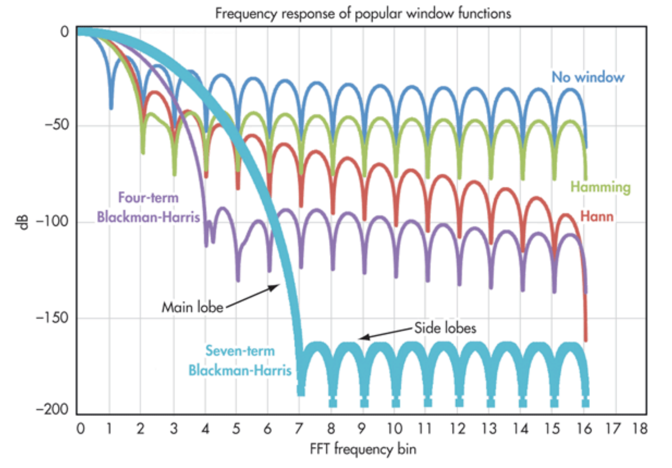
위 그림은 몇 가지 자주 사용되는 윈도우 함수들의 주파수 응답 곡선이다. 맨위는 윈도우를 적용하지 않은 것이고, 바로 아래의 초록색은 Hamming 윈도우 함수를 적용한 플롯이다. 그리고 다음에 보이는 것이 Hanning 윈도우를 적용한 결과이다. 특별한 이유가 없다면, 양호한 분해능과 높은 주파수 리키지가 낮아 적절한 균형을 이루고 있는 Hanning 윈도우가 적절하다.
hanning window
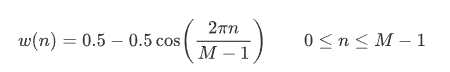
오스트리아의 기상학자인 Julius vos Hann의 이름을 따서 명명되었다.
hamming window
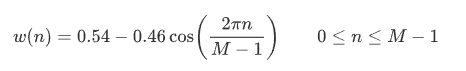
RW Hamming의 이름을 따서 명명되었으며, 시간 영역에서 절단된 자기공분산 함수를 평활화하기 위해 권장된다.
black harrison
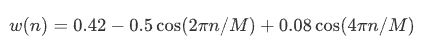
값을 평활화하기 기능.
3가지 윈도우 함수 모두 비슷한 값의 양상을 보이는 것을 확인할 수 있다.
출처: https://m.blog.naver.com/PostView.naver?isHttpsRedirect=true&blogId=lecroykorea&logNo=221549211257
