알고리즘
1.[2156] 포도주 시식

알고리즘 실력이 너무 바닥인 거 같다.. 오랜만에 복습 겸 초급 문제를 풀고 있는데 아직까지 제자리인 기분..ㅠㅠ알고리즘은 기계적인 외움보다 원리를 계속 고민해야하는 데 이 과정이 되게 어렵다...이 문제는 전형적으로 연속성을 따지는 문제 이다. 나는 2차원 배열로 풀
2.[11055] 가장 큰 증가하는 부분 수열

이 문제는 LIS의 기본적인 문제를 응용한 것인데, 나같은 알린이는 초기값때문에 많이 고생을 했다....여기에서 주목해야 할 것은 주석 처리한 di = ai 인데, 초기값으로 di = ai 를 갖고 있지않다면 다음과 같은 반례가 존재한다. 여기서 3 다음 2,1이 d
3.브루트 포스 - 순열

모든 순열을 구할 때 시간 복잡도는 O(N!)이다. 따라서 문제를 풀 때 n의 크기와 시간 제한을 주의 깊에 보아야 한다. c++같은 경우 , next_permutation , prev_permutation 을 이용하여 풀 수 있다.
4.브루트 포스 - 비트 마스크

not 연산을 하는 경우에는 자료형에 따라 달라 진다. 정수로 집합을 나타낼 수 있다. int 는 32비트 이기 때문에 2^32 즉, 4294967296을 넘어서면 안된다. 비트 마스크는 0~n-1 의 정수로 이루어진 집합을 나타낼 때 사용한다!! 1~n까지 정수는 공
5.[15663] N과 M (9)

재귀를 연습하기 위해서 풀어보았는데 너무 어려웠다..기록용으로 남겨놓는다.N과M 9번째 문제는 중복 제거가 핵심이다. 예를 들어 입력 케이스라 4 2 /9 7 9 1 라고 주어질 경우, 9가 두개 있다고 해서 1 9/ 1 9 로 두번 출력해서는 안된다. 위의 예시를 들
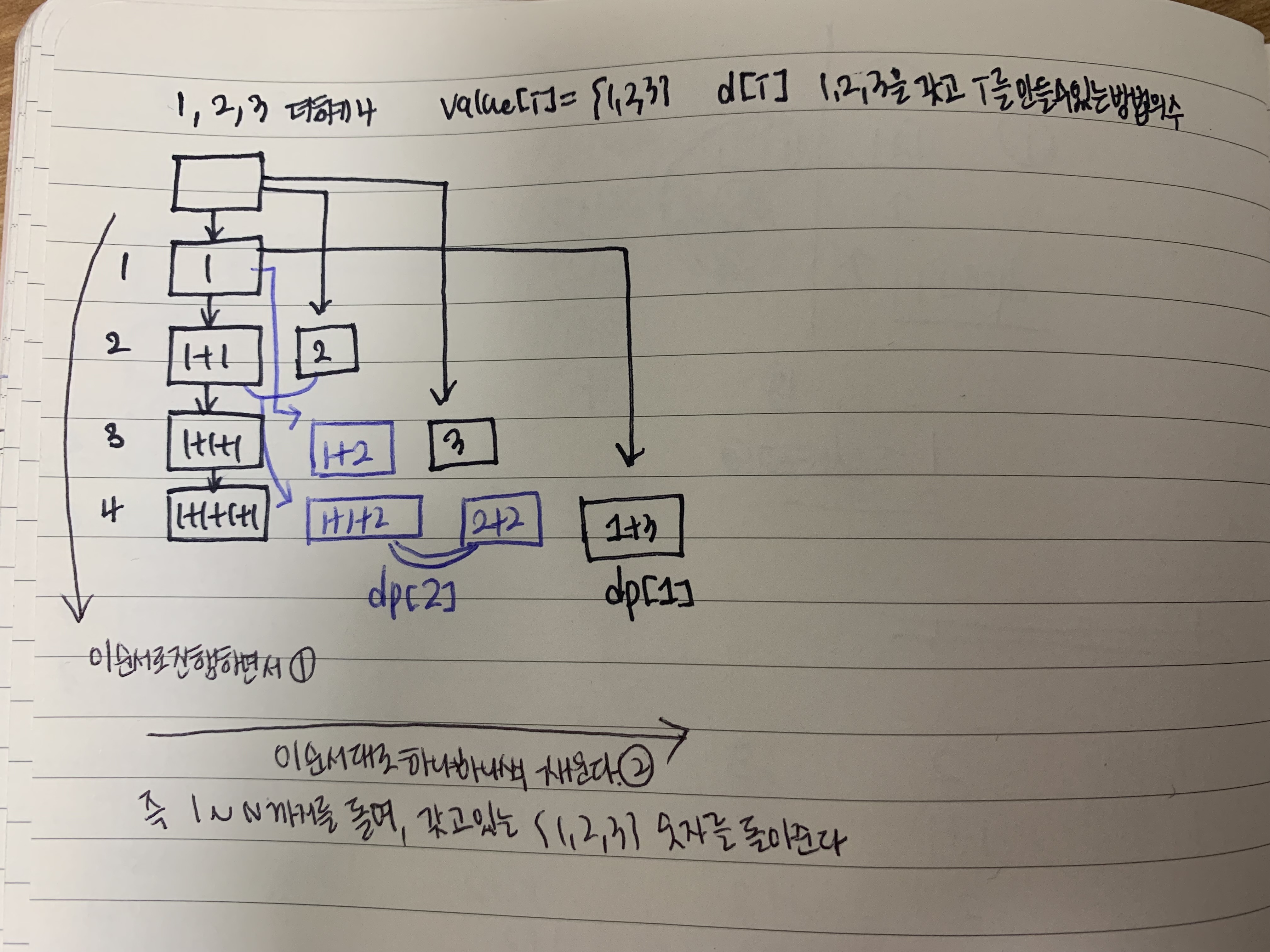
6.[9095] 1,2,3 더하기

재귀 방법을 이용해 풀어보았다\-void void hello(int target ,int sum) { if (sum == target) { count1++; } if (sum > target) return; hello(target, sum + 1); hello(tar
7.[1759] 암호 만들기

n과 m의 응용 문제 인듯 하다. 될 수 있는 거 다 뽑고 ( 브루트 포스) ,check 함수로 확인!!
8.[14889] 스타트와 링크

여름방학 때까지만 해도 코드를 이해하지도 못했는데 이제 스스로 구현할 수 있다니!! 뿌듯하당 ㅠㅠㅠ
9.[2529] 부등호

시간 초과 날 줄 알았는데 정답 되버렸다..다시 고민해야 겠다...
10.[1248] 맞춰봐

처음 : -10 ~ 10 까지 모든 수를 조합해서 수를 계산하면, 21^10 이 되어 시간 초과 발생한다. 2: 따라서 부호를 나눠봤는데 ai가 i==j 일때는 tempi 와 ai 의 부호가 같다. 따라서 경우를 나눠주면 +, - ,0 으로 10^10 으로 줄어든다.
11.16940

12.[16993] 벽 부수고 이동하기 3

1) 목표 : (1,1) 에서 (N,M) 으로 이동하는 최단 거리를 구하여야 함2) 조건 : k개 까지 벽을 깰 수 있고, 낮에만 벽을 깰 수 있다. 3) 입력 : N, M, K 를 받는다.4) 출력 : 최단 거리를 출력한다. 불가능할 때는 -1을 출력한다. 기존의 벽
13.[16954] 움직이는 미로 탈출

t초후 배열 만들기 (0초, ~ 8초까지, 8\*8 배열이므로)몇 초후에 내려가는 것이 중요하므로, 이를 check 배열에 설정해주어야함.bfs 돌리기.
14.[23743] 방탈출

스패닝 트리 : 모든 정점 포함, 순환 X 최소 스패닝 트리 : 가중치의 합을 최소로 만드는 스패닝 트리이를 위해, 크루스칼 알고리즘, 프림 알고리즘 등이 존재1) 간선의 가중치를 오름차순으로 정렬2) 가중치가 가장 작은 간선을 선택.3) 2개의 노드가 연결 되지 않았
15.[23741] 야바위 게임

bfs 를 활용하는 문제이다. 처음에 시도했을때 메모리 초과가 났는데, queue 에 중복된 것이 넣어지면 메모리 초과가 난다. 따라서, checki 함수를 통해 i번째 정점 중 tempcount 가 j 일때 방문하는 것을 기록함으로써 queue 의 중복을 방지해준다
16.세그먼트 트리

데이터가 연속적으로 존재할 때, 특정한 범위의 데이터의 합을 빠르고 간단하게 구할 수 있는 자료구조.만약 1~N 까지의 수의 합을 구하려면 선형적으로 계산을 하여야 하기에, 시간 복잡도가 O(N) 이 나온다. 하지만, 트리구조의 특성상, 세그먼트 트리는 O(logN)
17.[16236] 아기 상어

입력: 공간의 크기(2<=N<=20) 입력, 공간의 상태 입력 조건 : 아기상어 초기 2, 1초에 상하좌우 이동. 크기 자신 보다 작은 물고기만 먹을 수 있다. 물고기 없으면 종료. 물고기가 1마리 보다 많으면, 가까운 물고기. 가까운 물고기 중에서는 가장
18.배낭 문제

무게의 최대값이 정해져 있을때, 가치의 합이 최대가 되도록 짐을 고르는 문제물건을 쪼갤 수 있는 문제가치가 큰 물건 부터 담고, 남은 무게 만큼 무게를 쪼갠다. -> greedy 물건을 쪼갤 수 없는 문제동적 계획법으로 해결. dpi = i번째 물건까지 넣을 수 잇고,
19.다익스트라

다이내믹을 활용한 최단 경로 알고리즘. https://m.blog.naver.com/ndb796/221234424646출발 노드 설정출발 노드 기준으로 각 노드의 최소 비용 저장방문하지 않은 노드 중 가장 비용이 적은 노드 선택.해당 노드 거쳐서 특정 노드로
20.다익스트라 알고리즘 2

stl 을 이용하며 priority_queue<pair<int,int>> pq; 를 선언한다. pop 되는 순서 pair 에서 첫번째가 큰 순으로, 그 다음 두번째가 큰 순으로 나온다. O(ElogV)를 보장하여 해결할 수 있다.V는 노드 개수 E는 간선 개
21.[11779] 최소 경로 구하기 2

푸는 방법.1\. 기존의 다익스트라 알고리즘에서 경로만 추가되었다. 틀렸던 요인1\. INF 조정. 그리고 dist 배열의 자료형 (int 가 아닌 long long )
22.플로이드

모든 쌍의 최단 경로를 구하는 알고리즘for (int k=1; k<=n; k++) {for (int i=1; i<=n; i++) {for (int j=1; j<=n; j++) {if (di > di + dk) {di = di + dk;}}}}
23.[11404] 플로이드

24.[11780] 플로이드 2

전형적인 플로이드 알고리즘에 경로를 추가한 알고리즘이다. 다익스트라와 같이 플로이드 알고리즘은 간선의 next 를 정보를 저장하면 없는 간선을 next 로 가르키기 때문에 next 배열을 새로 만들어야 한다.
25.DAG

Directed Acyclic Graph사이클이 없는 방향 있는 그래프선행 관계가 있다.오직 DAG 를 할 수 있는 알고리즘그래프의 간선 u -> v 가 u가 v 가 먼저라는 의미일 때 정점의 순서를 찾는 알고리즘.어떤 정점 v의 순서에 추가되는 것은 u → v의
26.[1766] 문제집

bfs 를 활용한 위상 정렬 알고리즘이다. 여기서 주의 해야할 점은 최소 힙을 썼다는 것인데, 문제의 조건에 의하면 가능하면 쉬운 문제 부터 풀어야 한다라는 것이 있으므로, 가장 작은 수부터 큐에서 pop을 하여야 한다.
27.[1916] 최소비용 구하기

전형적인 다익스트라 알고리즘이다. 양방향 그래브가 아닌, 한 방향 그래프!계속 틀렸었는데 이유는 두가지가 있었다. 출발 노드에서 도착 노드로 갈때 가는 방법이 여러가지 일때 최소 비용으로 입력값을 받아야함. 이는 인접 리스트일 때는 상관이 없지만, 내가 쓰는 인접 행렬
28.최소 스패닝 트리

스패닝 트리 : 모든 정점 포함, 순환 X최소 스패닝 트리 : 가중치의 합을 최소로 만드는 스패닝 트리이를 위해, 크루스칼 알고리즘, 프림 알고리즘 등이 존재1) 간선의 가중치를 오름차순으로 정렬2) 가중치가 가장 작은 간선을 선택.3) 2개의 노드가 연결 되지 않았다
29.우선순위 큐 정렬 방식

priorty_queue<자료형, Container ,비교 함수> 변수명.https://travelbeeee.tistory.com/126
30.[1922] 네트워크 연결

우선순위 큐를 이용하여 선택되지 않은 정점을 연결하는 가장 작은 간선을 뽑는다.우선순위 큐의 작동 방식의 시간 복잡도가 O(log E) 이므로, 모든 간선을 push , pop 한다는 가정하에, 전체 시간 복잡도는 O(ElogE) 가 나온다.
31.벨만포드

a -> b 의 최단 경로는 정점의 개수를 n이라고 했을 때, 최대 n-1 개의 간선으로 이루어져 있다. from -> to (cost)
32.[1753] 최단 경로

다익스트라를 다시 구현해 보고 싶어서 풀어봤는데 시간초과로 되게 해맸다...;;입출력에 의해 시간 초과가 날 수 있다. 이 코드를 추가 시켜 줘야 한다. https://www.acmicpc.net/problem/15552우선순위 큐에 { 노드번호, 가중치 }
33.[11657] 벨만 포드

벨만포드 알고리즘이다long long 으로 해주어야 한다. aa\[edgesi.from] != INF 라는 조건을 추가해 줘야한다. 이어 지지 않았는데 만약 cost 가 음수면 INF+ cost 가 값이 더 작으므로 값이 업데이트된다. 음수 사이클을 체크 해줘야 한다.
34.[1865] 웜홀

https://www.acmicpc.net/board/view/72995
35.Stable sorting

같은 것이 있는 경우에 정렬하기 전의 순서가 유지되는 정렬 알고리즘. 시간복잡도가 nlogn 인 알고리즘에는 병합정렬이 있다. stable sorting 이 아닌 정렬 알고리즘은, 원래 순서를 의미하는 변수를 하나 더 저장해서 Stable sort 의 효과를 만들 수
36.[1377] 버블 소트

버블 소트가 몇 번째 횟수 만에 완성되는지 찾는 것인데, 문제에 있는 코드로는 버블 소트의 시간 복잡도가 O(N^2) 이므로 시간 초과가 난다. sort 를 O(nlogn) 만에 하고 인덱스 차이를 통해 비교한다. 즉, 뒤에 있던 숫자가 앞에 어느정도 까지 앞당겨 졌
37.[11048] 이동

나는 DP 가 너무 약하다.. 그래서 일단 저번에 풀던걸 복습하는 겸 풀어보았다. 문제
38.[11060] 점프점프

가장 왼쪽끝에 위치하고 가장 오른 쪽으로 가려고 할 때, 최소 점프 횟수 -> DP 다이내믹 프로그래밍을 이용한다. di = 위치 i 까지 이동했을때 걸리는 최소 점프 횟수따라서 1~ ai을 더한 만큼 i 가 이동할 수 있고 이를 j 로 놓았다.d i + j =
39.[15989] 1,2,3 더하기 4

1,2,3 더하기 문제와 다르게, 오름차순 정렬 된 것만 따진다. 따라서 다이내믹 배열을 1차원이 아닌 2차원으로 선언한다. di 은 i 의 합을 끝자리 1로 채웠다는 뜻이다. 따라서 i-1 원소에다가 +1 만 더해주면 된다. 따라서 식이 di = di-1 가 된다.
40.[12869] 뮤탈리스크

다이나믹으로 접근. dpik = scv 가 i 체력이 있고, scv 두번째가 j 체력이 있고, scv 세번째가 k 체력이 있을 때 공격해야 하는 최소 값. 이는 1,3,9 dpi-1k-9 + 1;1,9,3 dpi-1k-9 + 1;3,1,9 dpi-3k-9 + 1;3,9
41.[10422] 괄호

다이내믹으로 풀 수 있다. Ds = 길이가 s일때 올바른 괄호 문자열의 개수
42.15989, 2293
처음에 전에 접근했던 2차원 배열로 2293 문제를 풀어보려니, 메모리 초과가 났다. 이는 제한이 4MB 로 되어 있는데 dp10001 을 할당 받으니까, 10000 100 4 를 초과하기 때문.. 따라서 1차원 배열로 풀어야 했다. 15989 의 문제접근 방식을
43.[9251] LCS

다이나믹 프로그래밍
44.[2407] 조합
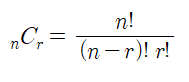
메모리 제이션을 이용하여, 계산 속도를 최적화 해야한다. 서로다른 n개에서 r개를 순서 상관없이 선택하는 경우의 수https://ko.wikipedia.org/wiki/%ED%8C%8C%EC%8A%A4%EC%B9%BC%EC%9D%98\_%EC%82%BC%EA%
45.[13549] 숨바꼭질 3

너비 우선 탐색을 이용중요한 것은 순간이동을 하면 0초가 걸리고, 순간이동을 하지 않는 이동은 1초가 더 늘어난다는 사실. 그래서 순간이동의 우선순위를 먼저 따져줘야함. 따라서 덱을 이용해서 순간이동을 front 에 집어넣고, 보통 이동은 back 에 집어넣어주므로써
46.[11660] 구간 합 구하기 5

다이내믹 프로그래밍, 구간 합 이용다이내믹 프로그래밍을 이용하여 0,0 부터 i,j 위치까지의 구간합을 di에 구한다. 이는 di = di-1 +di - di-1 +ai 로 구할 수 있다.(x1, y1) , (x2,y2) 가 주어졌으면 우리가 구하고자하는 넓이는 dx2
47.[2263] 트리의 순회

트리 pre, post, inorder 방식의 흐름을 직접 그려가며 코드를 작성한다. preorder 방식은 루트 -> 왼 -> 오 를 탐구하는 방식이다. inoder 방식은 왼 -> 루트 -> 오 를 탐구하는 방식이다. postorder 방식은 왼 -> 오 -> 루트
48.[2166] 다각형의 면적
다각형을 삼각형으로 쪼갠다. 삼각형 -> 신발끈 정리를 활용한다. x, y input 입력 받고각각의 삼각형 넓이구해주고더해서 출력x,y 처음에 int 로 받음. x,y가 큰 숫자일 경우, 오버플로우가 나서, double 의 형식으로 고쳐줌abs 를 맨마지막에 해줘야함
49.[2467] 용액

순차 탐색으로 o(n^2) 으로 시간 초과 가 난다. 이분탐색으로 시간 복잡도가 O(nlogn) 이다. 정렬함 (시간 복잡도 o(nlogn))sum = 두개 선택한 것만약 sum 이 음수라면, start 를 늘려줌. 양수로 가는 방향sum 이 양수라면, end 를 줄여
50.[1647] 도시 분할 계획

최소 스패닝 트리 - 프림 알고리즘임의의 정점하나를 선택. 연결된 모든 간선 우선순위 큐에 넣어줌.가장 작은 cost 갖는 노드 선택하고그 노드와 관련된 모든 간선 다시 우선순위큐에 넣어줌.모든 노드가 선택될 때 까지 반복. 최소 스패닝 트리 - 프림 알고리즘을 이용한
51.[2239] 스도쿠

해결 방법
52.구글 코드잼 2022

cf) 참고 https://blog.naver.com/pasdfq/22269042766542 개포 아카데미에서 평가가 안잡혀서 마침 코드잼을 하길래 풀어보았다..1,2,3 번은 풀었는데 4번을 풀다가 맞왜틀 과정을 겪고 빡쳐서 집에 왔다ㅎㅎㅎ어제 저녘에 풀라고
53.[13458] 시험 감독

자바로 한번 풀어볼 겸 쉬운 문제를 풀어보았다.
54.[28245] 배고파(Hard)
정말 많이 해맸다.풀고 나서 보니 왜이렇게 어렵게 생각했을까 싶다.최대 크기가 2^60 이므로 나이브하게 2^x + 2^y 에 해당하는 x와 y수를 구할 수 있다는 것만 알면 된다.처음에 이분탐색으로 풀으려고 했는데, 2^x+ 2^y 를 정확하게 딱 떨어지지 않는 수를
55.[28242]수학 선생님의 고민(Hard)

처음에 easy를 풀었을 때, n <= 5000 까지여서, 브루트 포스로 접근해야 겠다고 생각이 들었고, n^2 의 알고리즘으로 바로 풀렸다. 하지만 hard 같은 경우는 n<= 2n^6 이다. 이는 최적화를 시켜야 하고, 최적화를 시키는 방법중에서 나누어
56.[19638] 센티와 마법의 뿅망치
방법 PQ에 넣고 최대인 것 반으로 줄인 후 다시 넣는다. 코드 참고자료
57.[7570] 앱
https://www.acmicpc.net/board/view/6667
58.[14938번] 서강그라운드

맞왜틀 과정을 겪음. 결론적으로는 bfs 돌릴때 checktemp.num = true 다음에, total += arrtemp.num 을 했었는데, bfs 끝나고 나서, checki 될때 total += arri 을 하니 맞았다아마, 중복되어 가는 경우가 있나보다.
59.[5639] 이진검색트리
