Machine Learning with PyTorch and Scikit-Learn_chapter3

Loss function(손실함수)와 Cost function(비용함수).

• Loss function is usually a function defined on a data point, prediction and label, and measures the penalty. -> single data set에 대한 것.
• Cost function is usually more general. It might be a sum of loss functions over your training set plus some model complexity penalty (regularization). -> single data set의 합, entire data set에 대한 것.

=> A loss function is a part of a cost function
=> 크게 보면, 두 개념의 차이는 없음.

Objective function is the most general term for any function that you optimize during training.
MLE is a type of objective function (which you maximize)

https://stats.stackexchange.com/questions/179026/objective-function-cost-function-loss-function-are-they-the-same-thing

---

분류(또는 예측)을 위한 모델의 type(chapter3에 언급된 모델 기준).

1. Model-based Learning(모델을 생성하여 task 실시)

training data가 주어졌을 때, 분류/예측 모델을 구축.

새로운 데이터가 주어졌을 때, 이 분류/예측 모델로 output(분류/예측)을 도출.

• logistic regression
• Support Vector Machine
• Decision tress

1.1. Logistic Regression

1.2. Support Vector Machine

1.3. Decision tress

특정한 분류 규칙을 통해 데이터를 분류/회귀하는 모델.

Decision tree에서는 어떠한 질문(또는 정답)을 node라고 함.

• Root node: 첫 분류 기준이 되는 node
• Intermediate node: 중간 분류 기준이 되는 node # Root node와 Leaf node가 아닌 node
• Leaf node(terminal node): 마지막 node

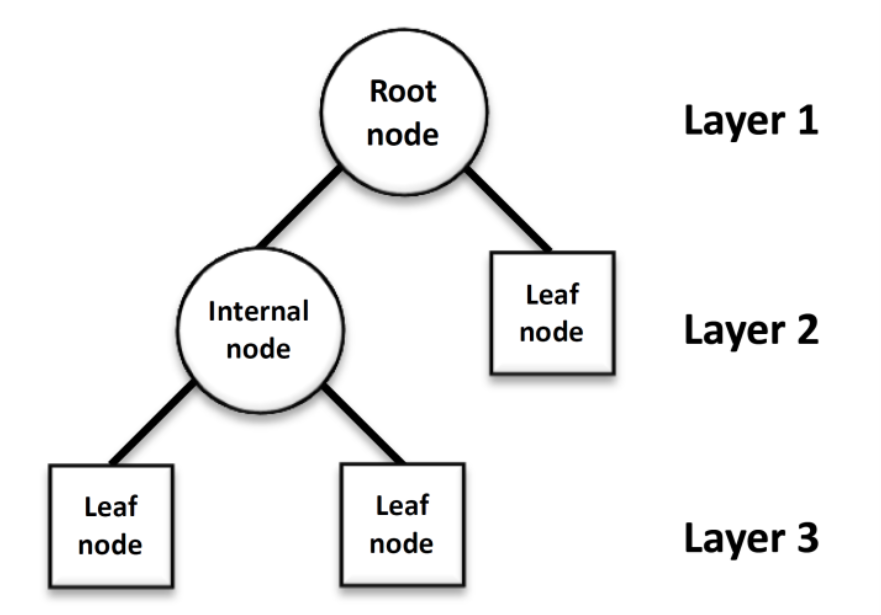
Decision tree의 main idea는 데이터를 2개 혹은 그 이상으로 분할하는 것. 또한 leaf node가 완전히 분류되게끔 하는 것.

• Decision tree의 성능을 평가하기 위해서는 Impurity(불순도)라는 개념을 알아야 함.
• 불순도(Impurity)란 같은 카테고리 안에 서로 다른 데이터가 얼마나 섞여 있느냐. 즉, 분리 후에 불순도가 낮을수록 결과가 좋은 것.
• 하위 node일수록, 불순도가 낮아져야 한다(그러하도록 설정해야 한다).
  - 부모 node와 자식 node의 불순도 차이를 Information Gain(IG)라 함.
  - 자식 node의 불순도가 작을수록, IG가 큰 것. IG를 최대화하는 것이 decision tree의 목적. 즉, Root node에서부터 leaf node까지 IG가 최대가 되도록 데이터를 분류.

불순도를 수치적으로 나타낼 수 있는 지표로는 아래의 3가지가 있음(decision tree_classification의 cost function)

1) Gini
2) Entropy
3) MisClassification error(책에서는 Classification error)

• Gini와 Entropy는 실질적으로 비슷한 tree 구조를 형성함. Gini가 계산량이 상대적으로 빠르기 때문에 기본값으로 좋음. 그러나 빈도가 높은 class를 한쪽으로 고립시키는 경향이 있음(entropy는 상대적으로 균형 잡힌 tree 구조를 형성).
• misclassification error는 Gini, entropy와 달리 미분이 불가능하여, 자주 쓰이지 않음.

leaf node의 순도가 100%(즉, 불순도가 0인)인 상태를 Full tree라고 함. 이렇게 되면, Decision tree의 모형이 너무 복잡해진다(즉, overfitting의 문제가 발생할 수 있음).

이를 해결하기 위해, node의 깊이를 제한하여 tree를 pruning(가지치기)함.

• 최대 depth 설정, leaf node 개수 제한, node 분할 기준 제한 등
• Decision tree에서 overfitting을 피하기 위해, pruning을 사용하는데 이 방법은 2가지로 나뉨.
  - Pre-pruning: tree를 다 그리기 전에 알고리즘을 멈춤.
  - Post-pruning: tree를 다 그린 후에 leaf node부터 가지치기를 실시.

Pruning의 cost function

CC(T) = Err(T) + α × L(T)

• CC(T)
  - 의사결정나무의 비용 복잡도
  - 오류가 적으면서 terminal node 수가 적은 단순한 모델일 수록 작은 값
• ERR(T)
  - 검증데이터에 대한 오분류율
• L(T)
  - terminal node의 수
• Alpha
  - ERR(T)와 L(T)를 결합하는 가중치
  - 사용자에 의해 부여됨, 보통 0.01~0.1의 값을 씀

Decision tree는 decision boundary가 데이터 축에 수직이어서 특정 데이터에만 잘 작동할 가능성이 높음. 이러한 단점을 보안하기 위해 나온 것이 Random forests.

Random forests: 같은 데이터에 대해 Decision tree를 여러 개 만들어 그 결과를 종합해 예측 성능을 높이는 기법. Random forests can be considered as an ensemble of decision trees.

https://ratsgo.github.io/machine%20learning/2017/03/26/tree/

2. Instance-based Learning(모델 생성 없이, 인접 데이터를 활용하여 task 실시)

새로운 데이터가 주어졌을 때, training data의 패턴을 파악하여 output(분류/예측)을 도출.

• K-Nearest Neighbor

2.1. K-Nearest Neighbor

• 어떤 데이터가 주어지면 그 주변(이웃)의 데이터를 살펴본 뒤 더 많은 데이터가 포함되어 있는 범주로 분류하는 방식
• 다른 지도학습 모델과 달리, 별도의 모델 구축(생성) 및 training data의 학습이 불필요함.
• 별도의 모델 구축 없이, task가 실행된다는 뜻에서 Lazy model이라고 함.

K-Nearest Neighbor 알고리즘을 사용할 때는 데이터들을 Noramlizaion 해주어야 함. 각 데이터의 특성을 나타내는 각각의 column의 scale이 다를 수 있기 때문.

KNN은 학습을 통해 결정되는 parameter가 없고, user define hyper parameter만 존재.

1) K: ‘가장 가까운 근접 이웃 데이터를 몇 개까지 탐색할 지.

• 1 <= K <= total data ea
• K가 너무 크면 overfitting, 너무 작으면 underfitting 문제 발생.
• optimal한 K는 K를 조정하면서 선택해야 함.

2) Distance Measures: 데이터와 데이터 사이의 거리를 어떤 방법으로 계산할 지.

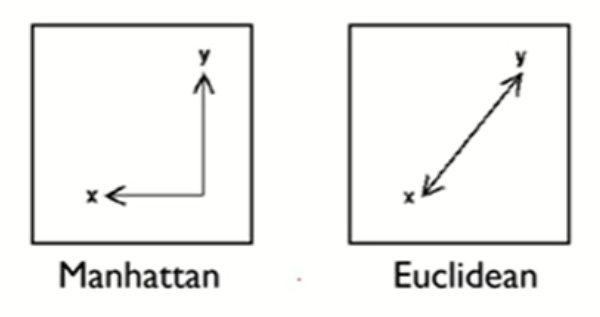
• Euclidean distance: 두 관측치(data point) 사이의 직선의 거리(두 벡터 사이의 직선의 거리; 피타고라스 정리).
• Manhattan distance: 두 관측치 사이의 격자를 통한 거리.
• Minkowski distance: generalization of the Euclidean and Manhattan distance.

3) Weighted: 새로운 데이터와 기존 관측치(data point) 간의 거리를 계산할 때 가중치를 고려하는 것. => Weighted KNN(데이터의 가중치를 고려하여 보다 정확하게 분류)

sklearn 기준, hyper parameter

1) n_neighbors: 탐색할 이웃의 수로 K를 의미함(default = 5).
2) metric: Distance Measures(default = minkowsi).
3) weights: 예측에 사용되는 가중치(uniform은 모두 동일한 가중치 부여, distance는 가까울 수록 더 가중치를 부여).
-> Gridsearchcv를 통해, 최적화된 parameter 탐색 가능.

KNN algorithm process

• Step0: input testing data & Normalize the data.
• Step1: Choose the number of K and a distance metric
• Step2: Find the k-nearest neighbors of the data record that we want to classify
• Step3: Assign the class label by ‘majority vote’
• Step4: print output

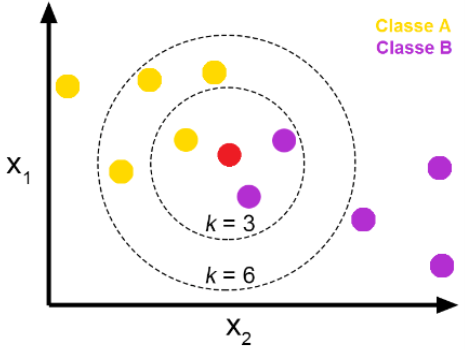
예), X_new(빨간점)가 주어졌을 때, 이를 A로 분류할지 B로 분류할지 판단. K=3일 때, X_new는 B로 분류. 반면, K=6일 때, X_new는 A로 분류. 즉, K가 무엇이냐에 따라 결과가 바뀜(default = 5).

• 인접한 K개의 데이터로부터 majority voting 시행하고 그 결과에 따라 X_new의 class가 정해지는 것.

KNN은 'curse of dimensionality'로 인해 overfitting 문제가 발생할 수 있음.

• KNN은 로지스틱 회귀처럼 overfitting 피하기 위해 regularization을 사용할 수 없음.

curse of dimensionality

• 데이터의 특징(feature)이 너무나도 많아서(차원이 커질수록 탐색해야할 공간이 늘어남) 성능 저하가 나타나는 현상.
• data set이 high-dimensional spaces를 갖으면, data point 간 거리가 멀어져(공간이 커지므로) 유사한 특징을 가지는 클러스터를 찾기 어려워짐.

curse of dimensionality 해결법.

1) 데이터의 양을 늘림: 데이터의 양이 증가할수록 밀도가 높아지므로, 데이터의 특징을 좀 더 잘 나타낼 수 있게 됨.

2) 차원 축소 기법 사용: PCA(Principal Components Analysis) 등의 방법을 사용하여 특징의 개수를 축소.

3) feature selection

https://www.youtube.com/watch?v=W-DNu8nardo
https://tobigs.gitbook.io/tobigs/data-analysis/python-knn
https://goofcode.github.io/similarity-measure