[BOJ][C#] 1389 케빈 베이컨의 6단계 법칙

LimJaeJun·2023년 12월 30일

PS/BOJ

목록 보기

79/108

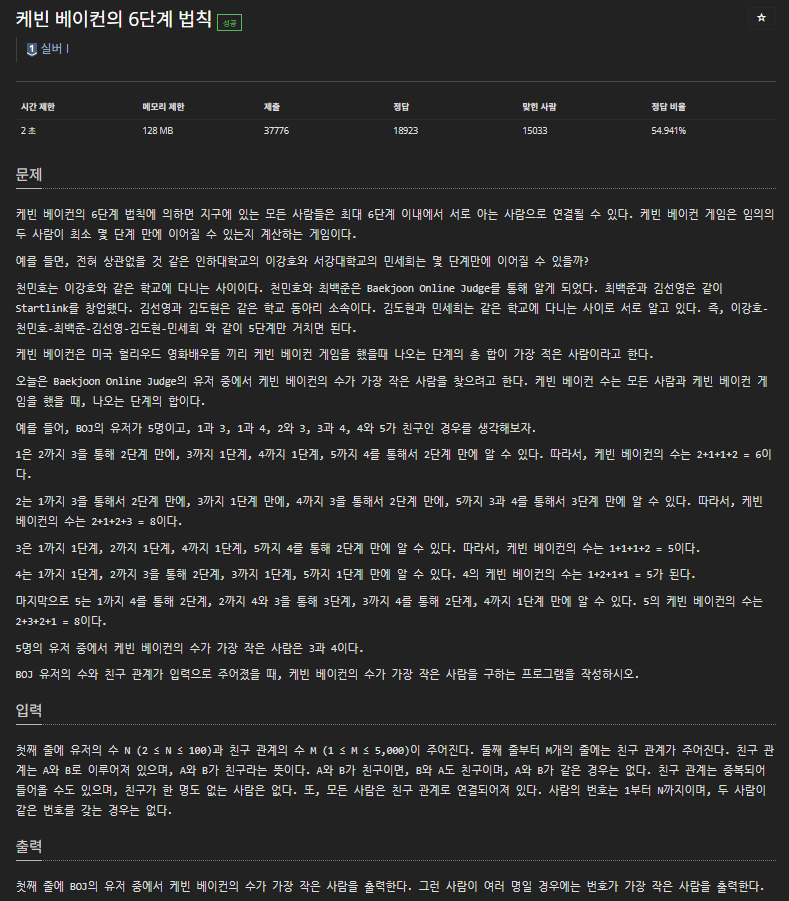
📕 문제

📌 링크

📗 접근 방식

친구 관계 그래프 생성:

입력으로 주어진 친구 관계를 그래프로 생성
딕셔너리를 사용하여 각 노드(사람)와 그에 인접한 노드(친구)들을 표현

BFS를 활용한 친구 거리 계산:

각 노드(사람)에 대해 BFS를 활용하여 해당 노드와의 친구 거리를 계산
CalculateFriendDistance 함수에서 BFS를 통해 각 노드까지의 최단 거리를 계산
거리가 array 배열에 저장되어 있으며, 해당 거리를 반환

친구 거리 계산 및 최소 거리 탐색:

모든 노드에 대해 친구 거리를 계산하고, 최소 거리를 갱신하는 방식으로 문제를 해결
최소 거리를 가진 노드를 출력

📘 코드

namespace BOJ
{
    class No_1389
    {
        static void Main()
        {
            int[] inputs = Array.ConvertAll(Console.ReadLine().Split(), int.Parse);
            int n = inputs[0];
            int m = inputs[1];
            
            Dictionary<int, List<int>> dict = new Dictionary<int, List<int>>();

            for (int i = 0; i < m; i++)
            {
                inputs = Array.ConvertAll(Console.ReadLine().Split(), int.Parse);
                int a = inputs[0]-1;
                int b = inputs[1]-1;

                AddFriend(a, b, dict);
            }

            int answer = 0;
            int count = int.MaxValue;
            for (int i = 0; i < n; i++)
            {
                int cnt = CalculateFriendDistance(i, n, dict);

                if (count <= cnt) continue;
                
                count = cnt;
                answer = i + 1;
            }

            Console.WriteLine(answer);
        }

        static int CalculateFriendDistance(int task, int n, Dictionary<int, List<int>> dict)
        {
            int[] array = new int[n];

            if (dict.ContainsKey(task) != true) return 0;
            
            foreach (var item in dict[task])
            {
                array[item] = 1;

                UpdateChildDistances(task, item, array, dict, 2);
            }

            return array.Sum();
        }

        static void UpdateChildDistances(int parent, int task, int[] array, Dictionary<int, List<int>> dict, int depth)
        {
            foreach (var item in dict[task])
            {
                if (item == parent)
                {
                    continue;
                }
                
                if (array[item] != 0 && array[item] <= depth)
                {
                    continue;
                }

                array[item] = depth;

                UpdateChildDistances(parent, item, array, dict, depth + 1);
            }
        }

        static void AddFriend(int a, int b, Dictionary<int, List<int>> dict)
        {
            dict.TryAdd(a, new List<int>());
            dict.TryAdd(b, new List<int>());

            dict[a].Add(b);
            dict[b].Add(a);
        }
    }   
}