[BOJ][C#] 5525 IOIOI

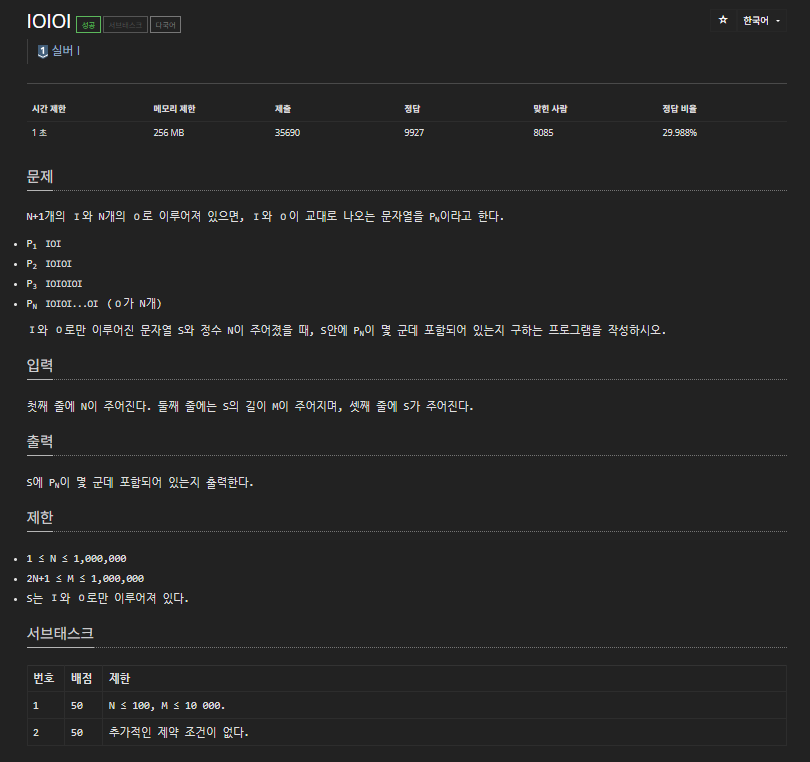
📕 문제

📌 링크

📗 접근 방식

첫번째 코드

패턴 매칭:

• 문자열 s에서 패턴 "IOI"를 찾아한다.
• "IOI" 패턴은 "IOIOI" 형태로 이어질 수 있으며, "I"와 "O"가 번갈아 나타나는 패턴

패턴 확인:

• 주어진 문자열 s를 처음부터 끝까지 탐색하면서 "I"가 나오면, 그 다음에 "O"가 나오는지 확인
• 이때, "IOI" 패턴이 발견되면 count를 증가
• "OI" 패턴을 고려하여 계속해서 탐색

결과:

• 반복된 패턴의 횟수가 n의 길이와 같다면 answer을 증가

두번째 코드

(KMP 알고리즘처럼 접근)
첫번째 코드의 접근방식과 굉장히 유사하다. 하지만 시간 복잡도로 접근해봤을때 첫번째 알고리즘은 O(MN)의 시간 복잡도를 가지지만 두번째 풀이로 접근한다면 O(M)의 시간 복잡도로 문제를 해결할 수 있다.
두번째 풀이의 핵심은 앞서 체크하였던 문자열을 기억하고 있다는 것이 굉장히 중요한 것 같다.

첫번째 풀이와 마찬가지로 "I"일때 다음이 "O"이고 그 다음이 "I"인지를 판단하며 해당 조건을 만족한다면 cnt를 증가시킨다.

만약 n이 3이고 문자열에서 세번 반복되었다면 "IOIOIOI"이 성립이 된 것이다.
"__IOIOI" 에서 다음이 "OI"가 된다면 한번 더 성립을 하기 때문에 cnt를 1감소하고 answer을 증가 시켜준다.

만약 "OI"가 반복되지 않았다면 다음에 이어서 체크를 할 수 없기 때문에 cnt를 초기화 시켜주었다.

📘 코드

첫번째 코드 (50점)

namespace BOJ
{
    class No_5525
    {
        static void Main()
        {
            int n = int.Parse(Console.ReadLine());
            int m = int.Parse(Console.ReadLine());
            string s = Console.ReadLine();
            int nLength = n * 2 + 1;

            int answer = 0;
            for (int i = 0; i <= m - nLength; i++)
            {
                if(s[i] == 'O') continue;

                int count = 0;
                for (int j = 0; j < nLength; j++)
                {
                    if (j % 2 == 0 && s[i+j] != 'I')
                    {
                        break;
                    }
                    
                    if (j % 2 == 1 && s[i+j] != 'O')
                    {
                        break;
                    }

                    count++;
                }
                
                if (count == nLength)
                {
                    answer++;
                }
            }

            Console.WriteLine(answer);
        }
    }   
}

두번째 코드 (100점)

namespace BOJ
{
    class No_5525
    {
        static void Main()
        {
            int n = int.Parse(Console.ReadLine());
            int m = int.Parse(Console.ReadLine());
            string s = Console.ReadLine();
            
            int answer = 0;
            for (int i = 0; i < m - 2; i++)
            {
                if(s[i] == 'O') continue;

                int cnt = 0;
                while (i < m - 2 && s[i + 1] == 'O' && s[i + 2] == 'I')
                {
                    cnt++;
                    if (cnt == n)
                    {
                        answer++;
                        cnt--;
                    }

                    i += 2;
                }
            }

            Console.WriteLine(answer);
        }
    }   
}

📙 오답노트

KMP 알고리즘에 대해서 좀 더 공부해야겠다.

📒 알고리즘 분류

• 문자열