[BOJ][C#] 3151 합이 0

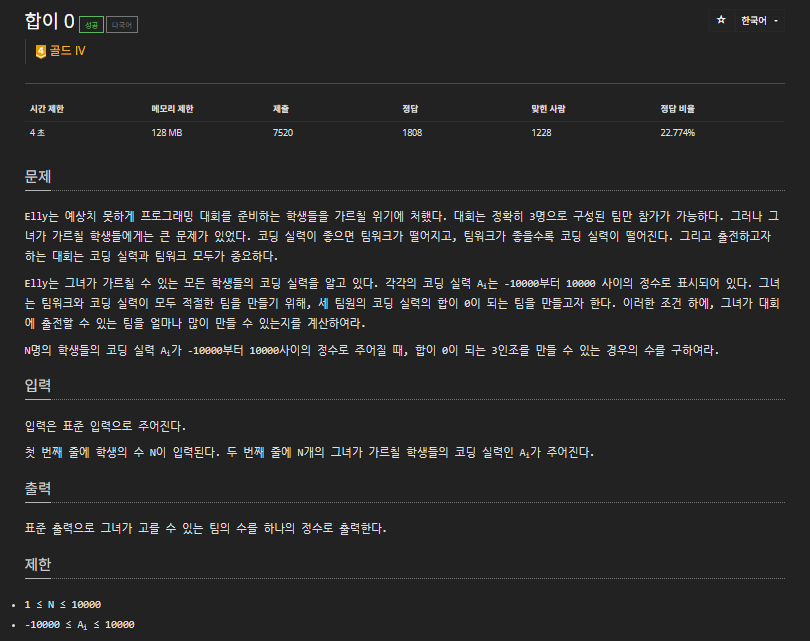
📕 문제

📌 링크

📗 접근 방식

정렬:

• 이분탐색을 해야하기 때문에 주어진 배열을 오름차순으로 정렬합니다.

삼중 합 세기:

• 삼중 합의 경우, 세 숫자의 합이 0이 되어야 합니다.
• 두 개의 수를 선택한 후, 나머지 하나의 수를 찾아야 합니다.
• 정렬된 배열을 기반으로 하여 투 포인터와 이분 탐색을 활용하여 문제를 해결합니다.

Lower, Upper Binary Search:

• 특정 값 이하(초과)인 수 중에서 가장 큰(작은) 인덱스를 찾는 두 함수를 정의합니다.
• 두 함수는 각각 이분 탐색을 통해 lower bound와 upper bound를 찾아내는 역할을 합니다.

삼중 합의 경우의 수 세기:

• 이중 반복문을 통해 두 개의 수를 선택합니다.
• 선택한 두 수의 합에 대응하는 음수 값을 이분 탐색으로 찾아냅니다.
• 찾아낸 음수 값의 lower bound와 upper bound의 차이를 계산하여 경우의 수를 더합니다.

📘 코드

using System.Text;

namespace BOJ
{
    class No_3151
    {
        static void Main()
        {
            int n = int.Parse(Console.ReadLine());
            int[] array = Array.ConvertAll(Console.ReadLine().Split(), int.Parse);

            Array.Sort(array);

            long answer = ThreeSumCount(array);

            Console.WriteLine(answer);
        }
        
        static long ThreeSumCount(int[] arr)
        {
            long count = 0;
            int n = arr.Length;

            for (int i = 0; i < n - 2; i++)
            {
                for (int j = i + 1; j < n - 1; j++)
                {
                    int target = -(arr[i] + arr[j]);
                    int lowerIndex = LowerBinarySearch(arr, target, j + 1, n - 1);
                    int upperIndex = UpperBinarySearch(arr, target, j + 1, n - 1);

                    if (lowerIndex != -1 && upperIndex != -1)
                    {
                        count += (upperIndex - lowerIndex + 1);
                    }
                }
            }

            return count;
        }

        static int LowerBinarySearch(int[] arr, int target, int x, int y)
        {
            int start = x;
            int end = y;
            int result = -1;

            while (start <= end)
            {
                int mid = (start + end) >> 1;

                if (arr[mid] >= target)
                {
                    result = mid;
                    end = mid - 1;
                }
                else
                {
                    start = mid + 1;
                }
            }

            return result;
        }

        static int UpperBinarySearch(int[] arr, int target, int x, int y)
        {
            int start = x;
            int end = y;
            int result = -1;

            while (start <= end)
            {
                int mid = (start + end) >> 1;

                if (arr[mid] <= target)
                {
                    result = mid;
                    start = mid + 1;
                }
                else
                {
                    end = mid - 1;
                }
            }

            return result;
        }
    }   
}

📙 오답노트

Upper에서 Lower를 뺀 이유는 같은 숫자가 존재할 수 있고 같은 수를 중복으로 선택이 가능하기 때문에 원하는 값의 최대 인덱스와 최소 인덱스가 필요하다고 판단하여 Upper과 Lower 코드를 제작하였다.

나의 코드는 두 수를 고를 상태에서 이분 탐색을 진행하기 때문에 $O(N^2 * log(N))$ 의 시간복잡도를 가지고 있는다. 사실 이 로직을 생각하고 작성하여 제출하였을 때, $N = 10000$까지 가능하기 때문에 최악의 경우 4초 이내에 수행하지 못할 것 같았지만 일단 제출해보자는 생각으로 코드를 작성하여 제출해보았더니 정답을 받아 약간 당황스러웠다. 다른 분들의 코드를 확인하고 (물론 C#으로 된 코드는 없었...) 다른 풀이를 이용하여 풀어봐야겠다.

📒 알고리즘 분류

• 브루트포스 알고리즘
• 정렬
• 이분 탐색
• 두 포인터