펭귄 몸무게 예측 - Regression

63.4% (78/123일)

남아공 케이프타운 인근 해변의 펭귄

빌 비숍의 저서 핑크펭귄

펭추리

1. 개요

• 펭귄들의 종, 서식 지역, 부리 길이와 부리 깊이, 날개, 성별, 그리고 몸무게 데이터 셋이 있는데, 이것을 다중 회귀 분석, 라쏘, 릿지 리그레션을 이용해서 몸무게를 예측하는 회귀 모델을 만들고, 어떤 독립변수가 가장 몸무게에 영향을 많이 미치는지 찾아내는 프로젝트

• 데이터 셋: https://www.kaggle.com/datasets/parulpandey/palmer-archipelago-antarctica-penguin-data

• 원본 데이터 columns (7개)
  species: 펭귄 종
  island: 서식지
  culmen_length_mm: 부리 길이
  culmen_depth_mm: 부리 깊이
  flipper_length_mm: 날개 길이
  body_mass_g: 몸무게 # 종속변수 y로 분리됨
  sex: 성별

• 다중 선형 회귀 : 독립 변수의 개수가 2개 이상인 선형 회귀 모델

• ridge, lasso : 다중 공선성 문제가 발생할 때, 이를 해결하기 위해서 사용됨

• 펭귄이 몸무게가 많이 나가는 조건을 우선 잘 먹기 위한 긴 부리를 가져야 할 것 같고, 날개가 길면 몸집이 커서 당연히 몸무게가 많이 나갈 것이라는 가설을 두고 분석해 보기로 함

• 펭귄 종별 파악
  . 젠투(Gentoo) 펭귄: 보통 5.9kg 황제>임금>젠투
  
  . 아델리(Adeliae) 펭귄: 보통 4.7kg, 길이 70cm
  
  . 턱끈(chinstrap) 펭귄: 보통 3~5kg
  

2. EDA 및 회귀분석

• 결측치 점검
  null값 sex항목 x_train(7), x_test(1) ---> fillna("neuter")

• 비수치값의 One-Hot Encoding
  species: 펭귄 종
  island: 서식지
  sex: 성별

• simple linear regression
  

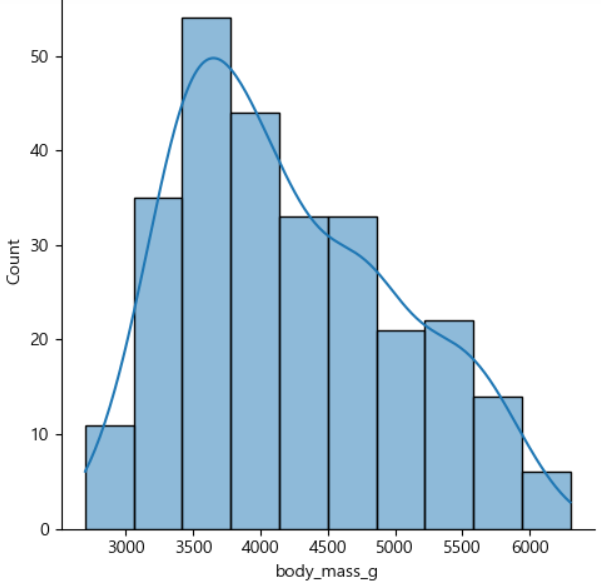
• x3_train.corr()["body_mass_g"].sort_values(ascending=False)
  body_mass_g 1.000000
  flipper_length_mm 0.871732
  species_Gentoo 0.825659
  culmen_length_mm 0.613607
  sex_MALE 0.416346
  sex_neuter -0.051560
  island_Torgersen -0.248728
  species_Chinstrap -0.301546
  sex_FEMALE -0.405928
  island_Dream -0.479264
  culmen_depth_mm -0.499075

• heatmap
  

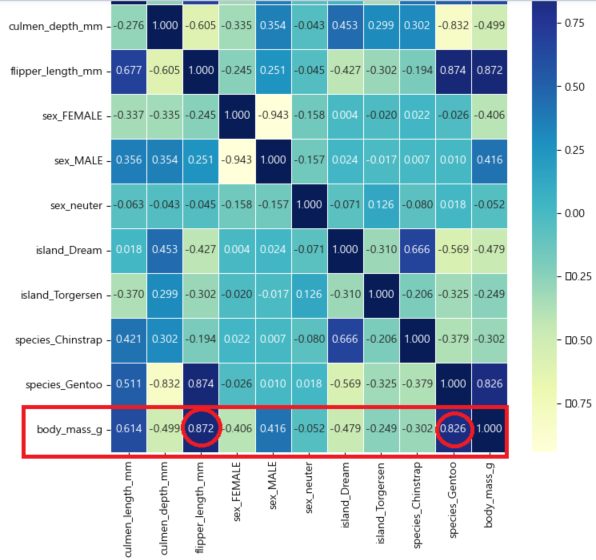
body_mass_g와 피어슨 상관계수가 높은 2개의 변수 flipper_length_mm, species_Gentoo 선택하여 각각을 독립 변수로 선택하여 테스트 해 봄

• 펭귄 종별 몸무게
  

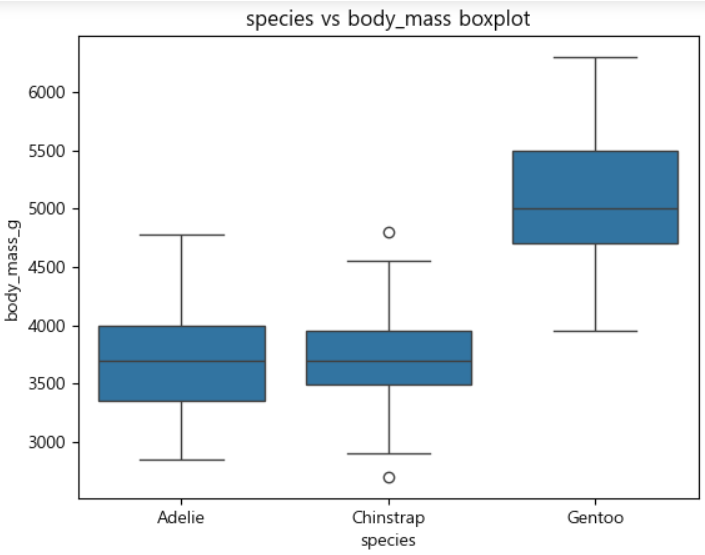
• 펭귄 종별 날개길이
  

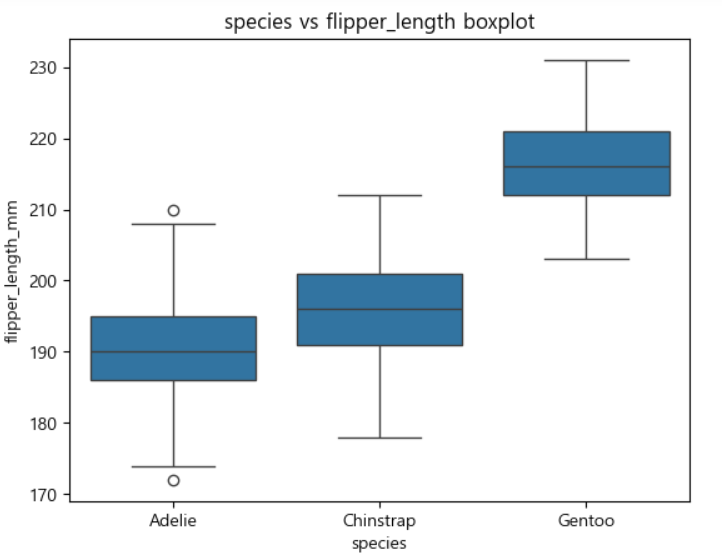
• 펭귄 종별 부리길이
  

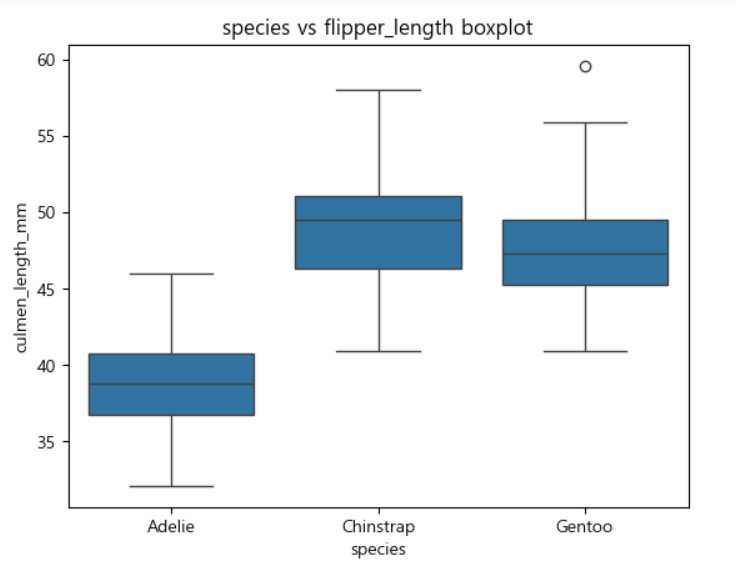
• 날개길이와 몸무게 간에 선형회귀모형을 적용해
  . OLS로 선형회귀 모델을 학습 결과:
  기울기: 49.887028625243126
  절편: -5822.600078017323
  x_train 데이터에 대한 시각화
  
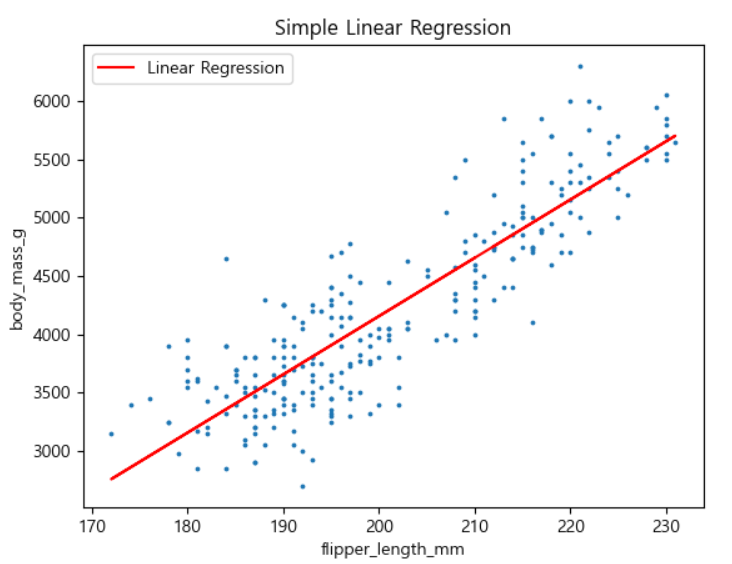
  x_test 데이터에 대한 시각화
  

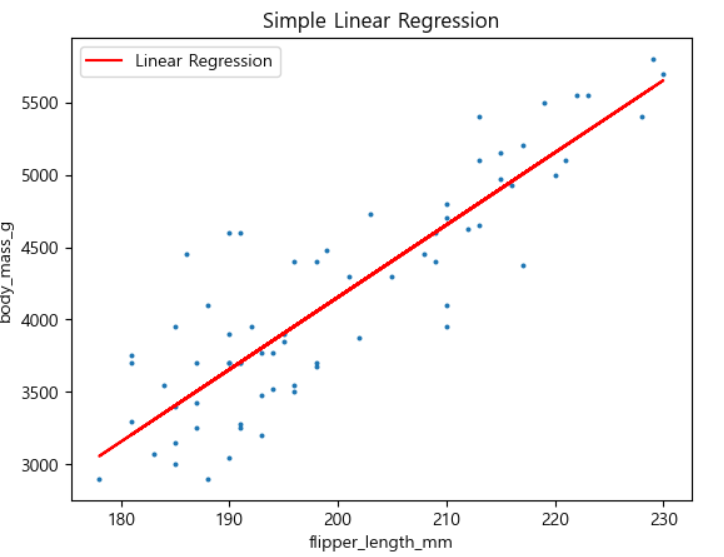
• R2, RMSE 두 가지 척도로 회귀식의 적합도를 측정
  train r2: 0.7599164415676609
  train RMSE: 396.8406480418189
  test r2: 0.7534381809067086
  test RMSE: 378.12237466205806

• 해석: 회귀 모델의 성능 평가에서 결정계수 train r2 점수는 이 모델이 데이터를 표현함이 75.99%이며, train RMSE: 396.8406는 예측 표준편차를 의미함

• OLS Regression Results

• OLS(Ordinary Least Squares)
  

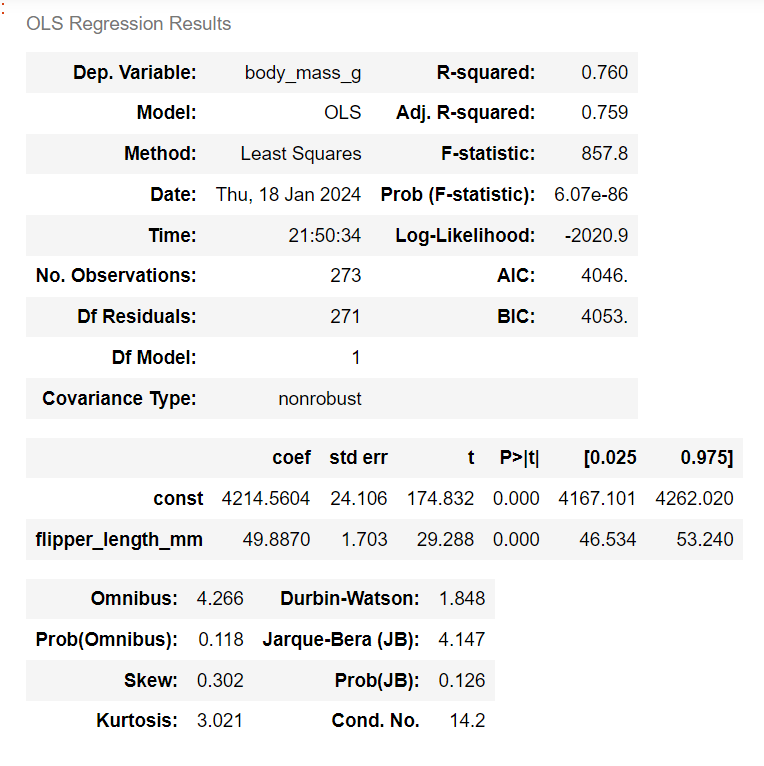
. R-squared를 보면 큰값이 나왔고, 추정된 회귀식이 총 변동량의 많은 부분을 설명 준다는 점은 좋지만, 과적합을 점검해 봐야 함. 너무 많은 특성과 복잡한 모델이 아닌지 점검

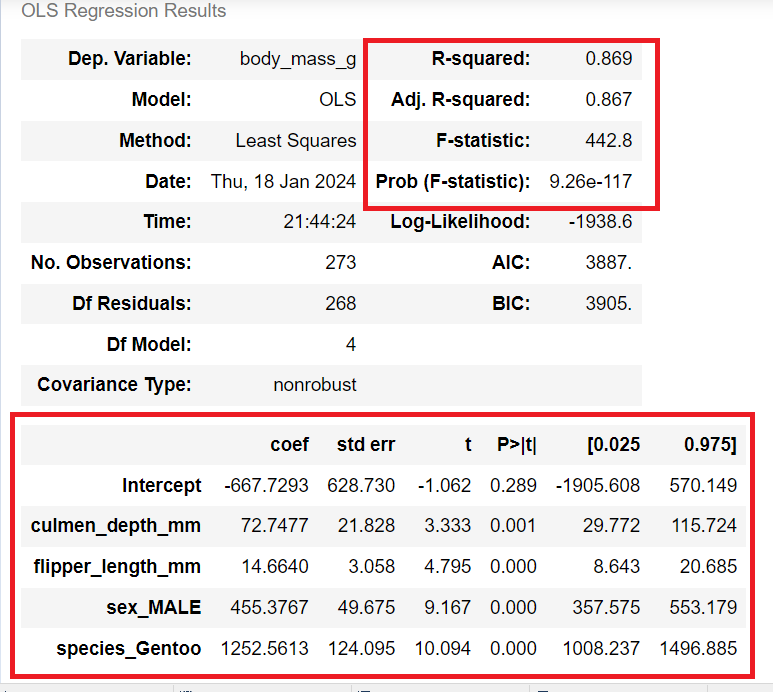
1. Dependent Variable: body_mass_g - 회귀 분석의 종속 변수는 body_mass_g
2. R-squared: 0.760 - R-squared 값은 0.760으로, 독립 변수들이 종속 변수를 설명하는 변동성의 76.0%를 나타낸다는 것을 의미
3. Model: OLS - 회귀 분석의 추정 방법은 최소제곱법(Ordinary Least Squares)
4. Adjusted R-squared: 0.759 - 조정된 R-squared 값은 0.759로, 모델의 적합성을 조정하여 나타냄
5. F-statistic: 857.8 - F-통계량은 857.8로, 회귀 모형의 전체 유의성이 매우 높음
6. Prob(F-statistic): 6.07e-86 - F-통계량의 확률값은 6.07e-86으로, 매우 작은 값이며, 이는 회귀 모형이 유의미함.즉, 독립변수가 종속변수에 통계적으로 유의미한 영향을 미친다는 것임.
7. coef, std err, t, P>|t|, [0.025, 0.975] - 독립 변수의 계수, 표준 오차, t-통계량, 관련 p-value, 그리고 95% 신뢰구간.
   계수는 flipper_length_mm이 1mm 증가할 때 body_mass_g의 예상 변화를 나타내며, flipper_length_mm의 계수는 49.8870으로, flipper_length_mm이 1mm 증가할 때마다 body_mass_g가 49.8870g 증가 예상
8. Omnibus: 4.266, Durbin-Watson: 1.848 - Omnibus 테스트는 회귀 모형의 전반적인 적합성을 테스트하며, Durbin-Watson 테스트는 자기상관(autocorrelation)의 존재를 검사함
9. Jarque-Bera (JB): 4.147, Skew: 0.302, Kurtosis: 3.021, Prob(JB): 0.126 - Jarque-Bera 테스트는 잔차의 정규성(normality)을 검사하며, Skew와 Kurtosis는 잔차의 비대칭성과 왜도성을 나타냄. 이 경우, Jarque-Bera 테스트의 p-value가 0.126으로 크므로, 잔차가 정규 분포를 따른다고 결론 내릴 수 있음
10. Cond. No.: 2.87e+03 - 조건 수는 회귀 모형의 조건 수를 나타내며, 이 값이 크면 회귀 분석의 안정성이 낮을 수 있음.
11. Log-Likelihood: -2020.9 - Log-likelihood는 모델의 우도 함수의 자연로그 값이며, 음수이므로 최종 값은 양수. 이 값은 모델이 데이터를 얼마나 잘 설명하는지를 나타낸다. Log-likelihood가 높을수록 모델이 데이터를 더 잘 설명한다고 볼 수 있다.
12. AIC: 4046 - AIC (Akaike Information Criterion)는 모델의 복잡도를 고려한 적합도 지표. AIC 값은 모델 선택과 비교에 유용함. 일반적으로, AIC 값이 낮은 모델이 더 적합한 모델로 간주됨.
13. BIC: 4053 - BIC (Bayesian Information Criterion)은 AIC와 유사하지만, 모델의 복잡도에 더 큰 패널티를 부여함. BIC 값이 낮은 모델이 더 적합한 모델로 간주됨.

• 11~13은 모델의 적합도와 복잡도를 평가하는 데 사용되며. Log-likelihood가 높고, AIC와 BIC 값이 낮을수록 모델이 더 적합한 것으로 간주됨

• 선형 회귀 모델은 오차에 대한 몇 가지 가정을 하고 회귀식을 도출했음.
  . 오차항(𝜖𝑖)의 평균은 0이고 분산은 𝜎2이다. (등분산성)
  . 오차항(𝜖𝑖들은 서로 독립이다. (독립성)
  . 오차항𝜖𝑖은 정규분포를 따른다. (정규성)

• skewness
  . 확률 분포가 중심으로부터 치우친 정도
  . 양수일 경우엔 왼쪽, 음수일 경우엔 오른쪽으로 치우친 형태
  . 절대값이 2보다 작으면 정규분포에서 크게 벗어나지 않는다고 봄
  . 값이 0.302인 이 피처는 약간 오른쪽으로 치우쳐 있는 분포

• kurtosis
  . 확률 분포가 중심으로 몰려서 뾰족한 정도
  . 양수면 정규분포보다 뾰족하고 음수면 정규분포보다 완만
  . 절대값이 7보다 작으면 정규성을 벗어나지 않는다고 봄
  . 값이 3.021인 이 피처는 일반적인 정규 분포보다 꼬리 부분이 뾰족한 분포

• 다중 선형 회귀 분석(multiple linear regression)
  . 먼저 k개의 독립변수마다 각각 단순 회귀 모형을 만든다.
  . 여기서 SSR이 크거나, SSE가 작거나, F 값이 크거나, t 값이 크거나 R^2 값이 큰 것을 기준으로 적합이 제일 잘 된 것을 선택한다
  . 전진 선택법 및 후진 제거법 시행

다중 선형 회귀 분석(multiple linear regression)

다중 선형 회귀 모델에서 전진 선택법과 후진 제거법 적용 최적화

(A) 전진 선택법으로 독립변수 적용

• x_train data 확인
  

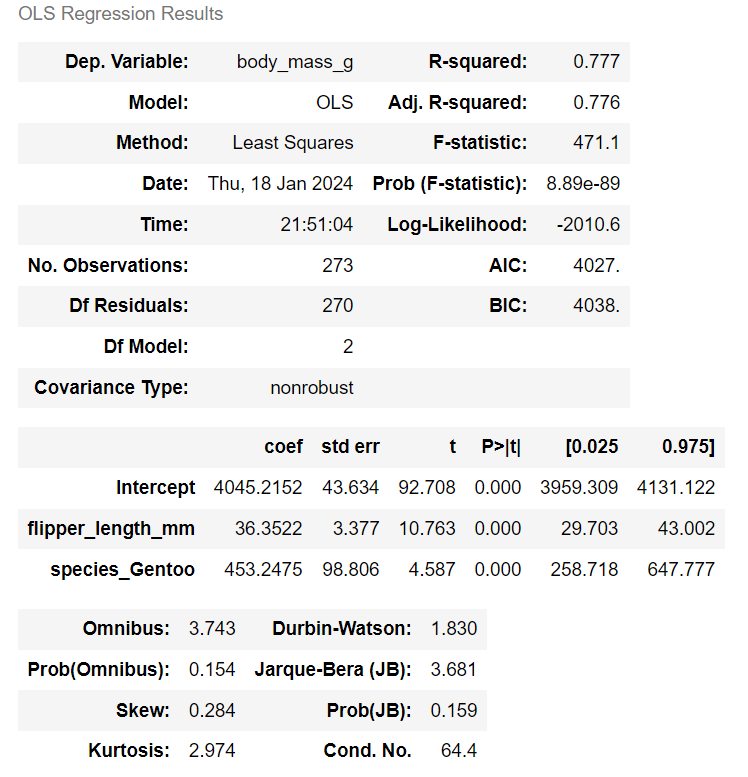
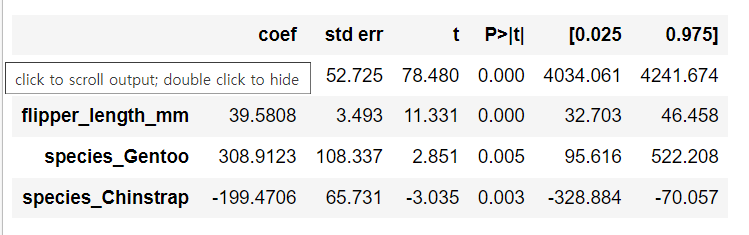
(B) 후진 제거법에 의한 최적 독립변수 도출

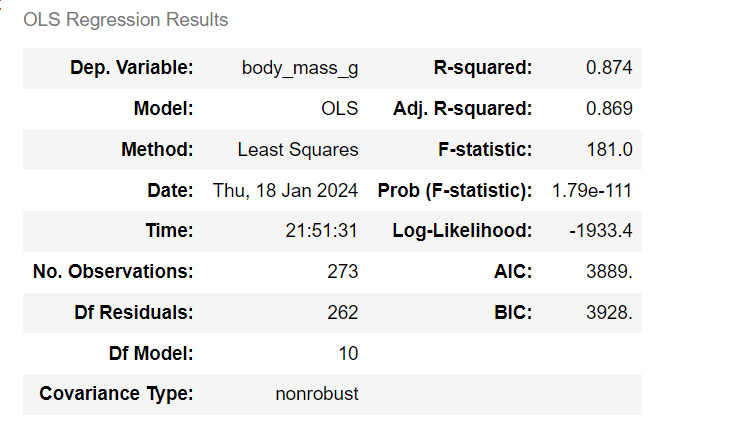
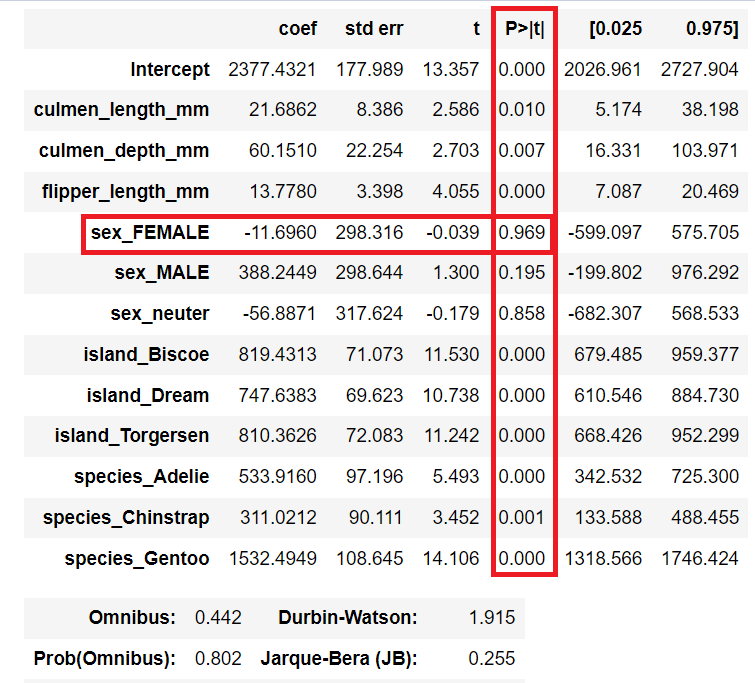
독립변수 단계별 제거

• P>|t| 큰값 및 VIF 진단
• 1) drop sex_FEMALE P>|t| 0.969
  . R-squared: 0.874, F-statistic: 181.0
• 2) drop sex_neuter P>|t| 0.696
• 3) drop island_Biscoe P>|t| 0.000
• 4) drop island_Torgersen P>|t| 0.855
• 5) drop island_Dream P>|t| 0.239
• 6) drop culmen_length_mm
• 7) drop species_Chinstrap
• 8) drop species_Adelie

당초 잘못된 x_train OLS결과

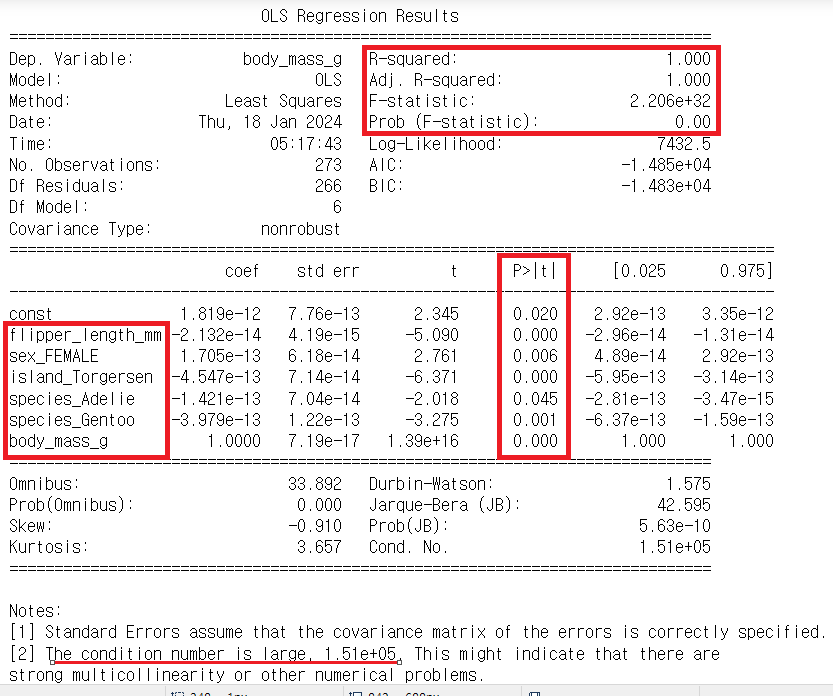
여기서, 1.819e-12는 절편(intercept)이며, flipper_length_mm, sex_FEMALE, island_Torgersen, species_Adelie, species_Gentoo의 계수는 각각 -2.132e-14, 1.705e-13, -4.547e-13, -1.421e-13, -3.979e-13입니다.

body_mass_g를 독립변수로 잘못 들어가서 계수가 음수값이 나와 버렸다.

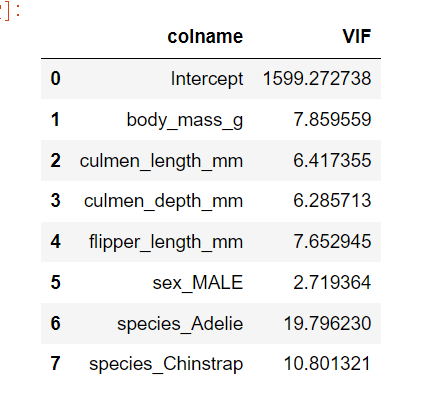
VIF를 이용한 다중 공선성 점검

다중 공선성이 발생시키는 문제 : 파라미터 추정의 불안정성, 해석의 어려움, 적절한 가중치를 찾지 못하고 변수들에 대해 과도한 가중치 크기를 할당하는 경향 등

• 분산 팽창 계수(VIF) 확인(10 이상)하여 관련 변수 점검

• 이전 후진 제거법으로 처리한 독립변수 확인
  

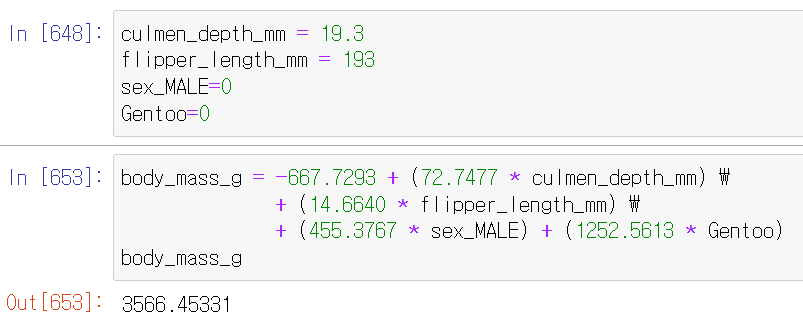
• 최종단계 OLS
  
  

Ridge, Lasso Regression

• Lasso regression: 여기에 정규화를 위해서 회귀 계수들의 절대값의 합을 더해줌. L1 regularization이라고도 함.

• Ridge regression은 정규화를 위해서 회귀 계수들의 제곱 합을 더해줌. L2 regularization이라고도 함.
  

회귀 분석 결과

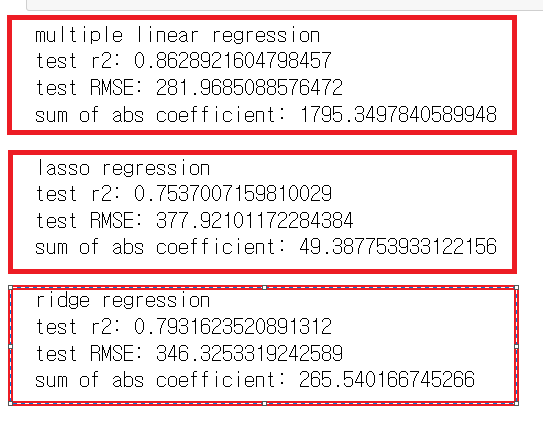
1) 다중선형회귀(multiple linear regression)

• test R2: 0.8629 - 독립 변수들이 종속 변수를 86.29% 설명할 수 있음
• test RMSE: 281.97 - 모델의 평균 제곱근 오차는 281.97. 모델의 예측 정확도를 나타냄
• sum of abs coefficient: 1795.35 - 다중선형회귀 모델에서 수의 절댓값의 합은 1795.35. 각 독립 변수의 영향력의 크기를 나타냄.

2) Lasso

• test R2: 0.7537 - Lasso 회귀 모델의 설명력은 75.37%
• test RMSE: 377.92 - 모델의 평균 제곱근 오차는 377.92이며, 모델의 예측 정확도를 나타냄
• sum of abs coefficient: 49.39 - 계수의 절댓값의 합 49.39

3) Ridge

• test R2: 0.7932 - Ridge 회귀 모델의 설명력은 79.32%
• test RMSE: 346.33 - 평균 제곱근 오차는 346.33
• sum of abs coefficient: 265.54 - 계수의 절댓값의 합은 265.54

3. 마무리

다중 선형 회귀 분석 결과, 부리 깊이, 날개 길이, 성별, 종별이 증가함에 따라 몸무게 증감에 계수를 찾아내고, 그에 대한 검증을 해 봤음

다중공선성과 변수 선택을 위해 라소와 릿치 모델을 돌렸더니 양호하다고 나왔다.

결론적으로, 부리의 깊이, 날개 길이, 성별, 종별이 펭귄의 몸무게에 영향을 미치는 주요 독립 변수로 확인되었으며, 라쏘와 릿지 회귀 모델을 통하여 다중공선성 및 모델의 해석력과 안정성을 향상시킬 수 있다는 것을 인지하였음

• 개선사항
  . 교차 검증(Cross-Validation) 등을 통해 보다 향상된 모델 성능 평가
  . 다양한 기법을 숙달하여 보다 확실한 독립변수 선택 능력 강화
  . 모델의 성능 최적화, RMSE를 줄이고, 모델 예측력 향상을 위한 노력