문제 : https://www.acmicpc.net/problem/11066
풀이
dp를 이용해 해결하는 문제이다.
최소비용은 책이 n권있다고 가정할 때, 매번 합칠때마다 비용이 중첩되어 발생한다
즉, 1~n권까지의 각각의 책의 비용+매번 합칠때 드는 비용 = 최소비용이다.
dp[i][j]=i에서 j까지의 최소비용으로 점화식을 계산한다.
최소비용의 계산방법은 아래와 같다
**편한 계산을 위해 idx는 1부터 시작하게 임의로 설정했습니다.
주어진 크기가 li=[0,40,30,30,50,20]인 예시로 확인해본다.
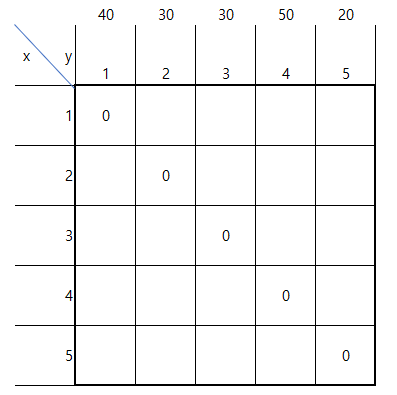
책을 합치는 구간이 1일때,
먼저, dp[i][i]=는 존재하지않는다.(합치지 않아 비용이 발생하지 않으므로)
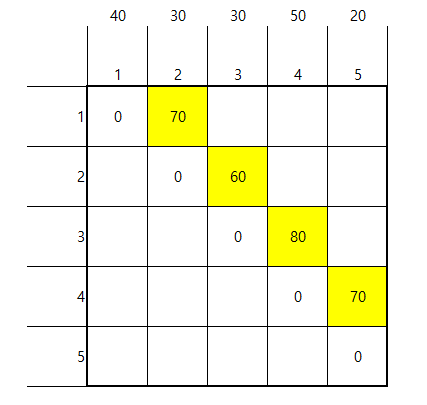
책을 합치는 구간이 2일때,
- dp[1][2]=li[1]+li[2]
- dp[2][3]=li[2]+li[3]
- ... dp[i][i+1]=li[i]+li[1] 이다.
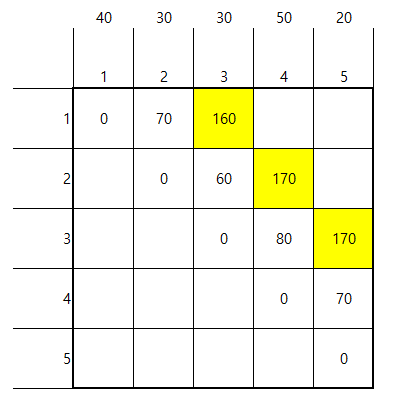
책을 합치는 구간이 3일때,
- dp[1][3]=1+(2+3)의 방법과 (1+2)+3의 방법중 최소값이므로
=min(dp[1][1]+dp[2][3],dp[1][2]+dp[3][3])+li[1]+li[2]+li[3]
=min(0+70,60+0)+40+30+30 = 160 - dp[2][4]=위와 동일하게 계산.
=min(dp[2][2]+dp[3][4],dp[2][3]+dp[4][4])+li[2]+li[3]+li[4]
=170 - dp[i][i+2]=min(dp[i][i]+dp[i+1][i+2],dp[i][i+1])+sum(li[2]~li[4])
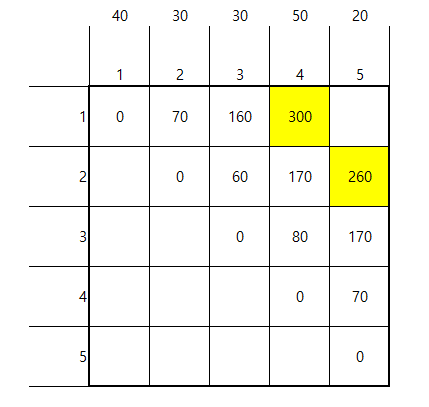
책을 합치는 구간이 4일때,
- dp[1][4]=min(dp[1][1]+dp[2][4],dp[1][2]+dp[3][4],dp[1][3]+dp[4][4])+sum(li[1]~li[4])
=300 - dp[2][5]=min(dp[2][2]+dp[3][5],dp[2][3]+dp[4][5],dp[2][4]+dp[5][5])+sum(li[2]~li[5])
- dp[i][i+3]=min(dp[i][j]+dp[j+1][i+3])+sum(li[i]~li[i+3]), j는 i부터 i+3까지
즉, 점화식을 작성해보면
dp[i][i+k]=min(dp[i][j]+dp[j+1][i+k])+sum(li[i]~li[i+k]), j는 i부터 i+k까지
이때, 뒤의 sum(li[i]~li[i+k])는 매번 연산해줄필요 없이 li[i]번까지의 합인 배열 sums[i]를 미리 만들어서 계산해주면 시간단축에 용이하다.
즉,
sum(li[i]~li[i+k]) -> sums[i+k]-sums[i-1] (sums[i]는 1부터 i까지의 합)
import sys
input=sys.stdin.readline
T=int(input())
for _ in range(T):
K=int(input())
li=[0]+list(map(int,input().split()))
dp=[[0]*(K+1) for _ in range(K+1)]
sums=[0]*(K+1)
for i in range(1,K):
dp[i][i+1]=li[i]+li[i+1]
sums[i]=sums[i-1]+li[i]
sums[K]=sums[K-1]+li[K]
for k in range(2,K+1):
for i in range(1,K+1):
if i+k>K:
break
min_v=10**9
for j in range(i,i+k):
min_v=min(min_v,dp[i][j]+dp[j+1][i+k])
dp[i][i+k]=min_v+sums[i+k]-sums[i-1]
print(dp[1][K])