Convolution

wyj·2023년 3월 31일

Computer Vision Convolution Cross Correlation

Infroduction to Computer Vision

목록 보기

1/2

공간 기반 영상 처리

공간 기반 영상 처리는 처리 대상 점의 주변 픽셀들의 밝기 값을 고려해서 대상 점의 밝기 값을 결정하는 처리입니다.

마스크(mask)는 처리 대상 점의 주변 픽셀들의 밝기 값을 나타내기 위한 사각형이며, 커널(Kernel)이나 필터(filter)로도 불립니다.

마스크는 보통 좌우대칭이며 홀수 크기의 형태를 가집니다.

필터링 (Filtering)

처리 대상 점의 주변 픽셀들을 결합하는 것을 필터링이라고 합니다.

필터링을 통해서 이미지로부터 더 유용한 정보를 얻거나, 노이즈를 제거하거나, 경계선을 뚜렷하게 만드는 작업을 할 수 있습니다.

필터링은 딥러닝의 합성곱 신경망(Convolution Neural Network, CNN)의 핵심 연산이기도 합니다.

선형 필터링 (Linear Filtering)

필터링의 단순한 버전으로 선형 필터링이 있습니다.

선형 필터링은 각각의 처리 대상 점을 이웃한 픽셀 값들의 선형 결합(Linear Combination)으로 대체하는 것입니다.

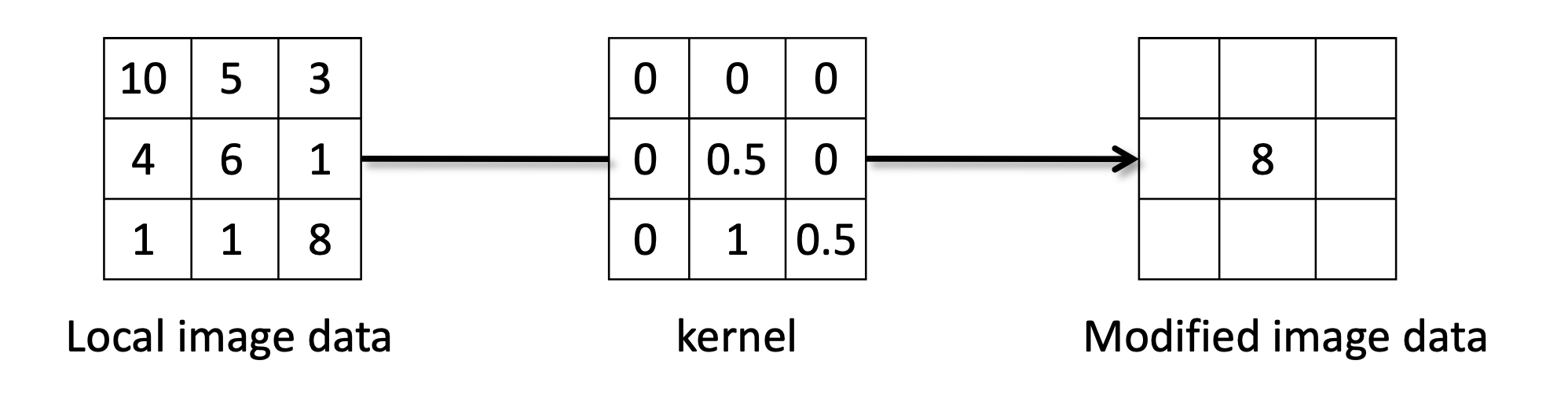
평균값 필터링 (Mean Filtering)

평균값 필터링은 대상 픽셀을 이웃 픽셀들의 평균값으로 대체하는 것입니다.

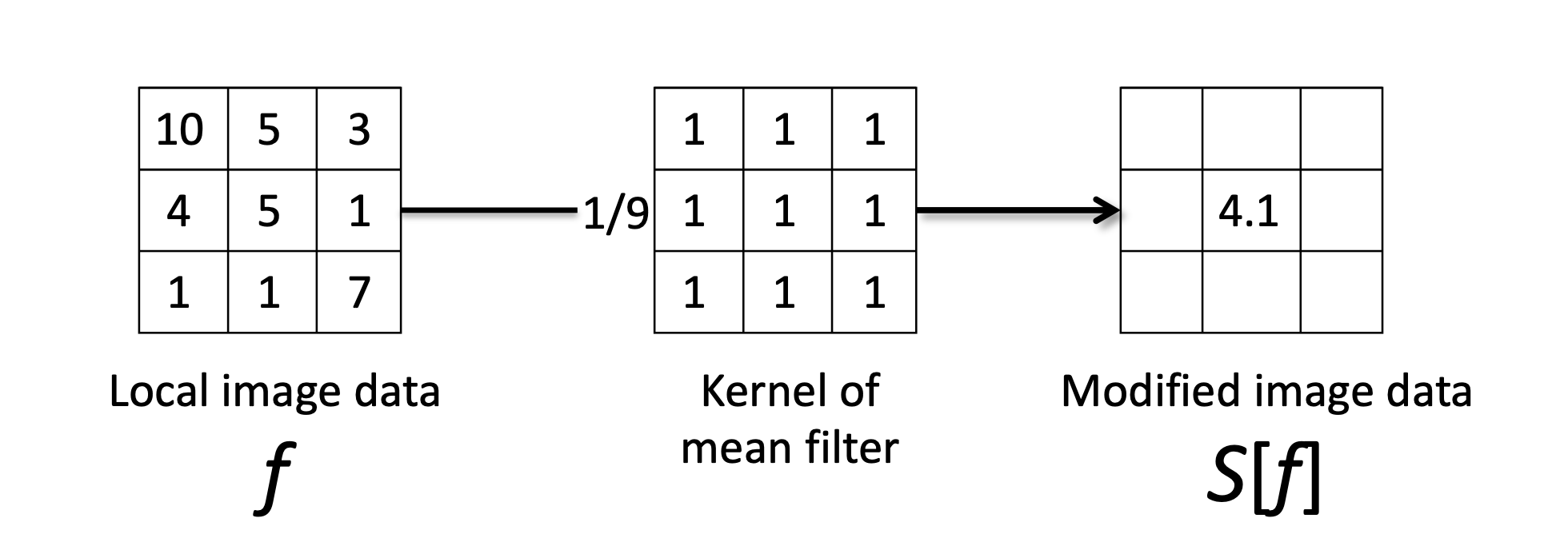
이미지 $f$ 가 있을 때, 평균 필터링 커널을 적용하면 변형된 이미지 $S[f]$ 를 얻을 수 있습니다.

평균값 필터링의 수식은 다음과 같습니다.

S[f](m,n)=\sum_{i=-1}^{1}\sum_{j=-1}^{1}f(m+i,n+j)/9

이미지 $f$ 의 9개 픽셀을 모두 더한 다음, 픽셀 개수만큼 나누는 간단한 작업임을 알 수 있습니다.

일반적으로 커널의 크기가 k인 경우 평균값 필터링의 수식은 다음과 같습니다.

S[f](m,n)=\sum_{i=-k}^{k}\sum_{j=-k}^{k}w(i,j)f(m+i,n+j)

위의 수식에서 $w(i,j)=1/(2k+1)^2$ 입니다.

Convolution and Cross-Correlation

커널을 이미지에 적용하는 연산으로 Convolution과 Cross-Correlation이 있습니다.

Cross-Correlation

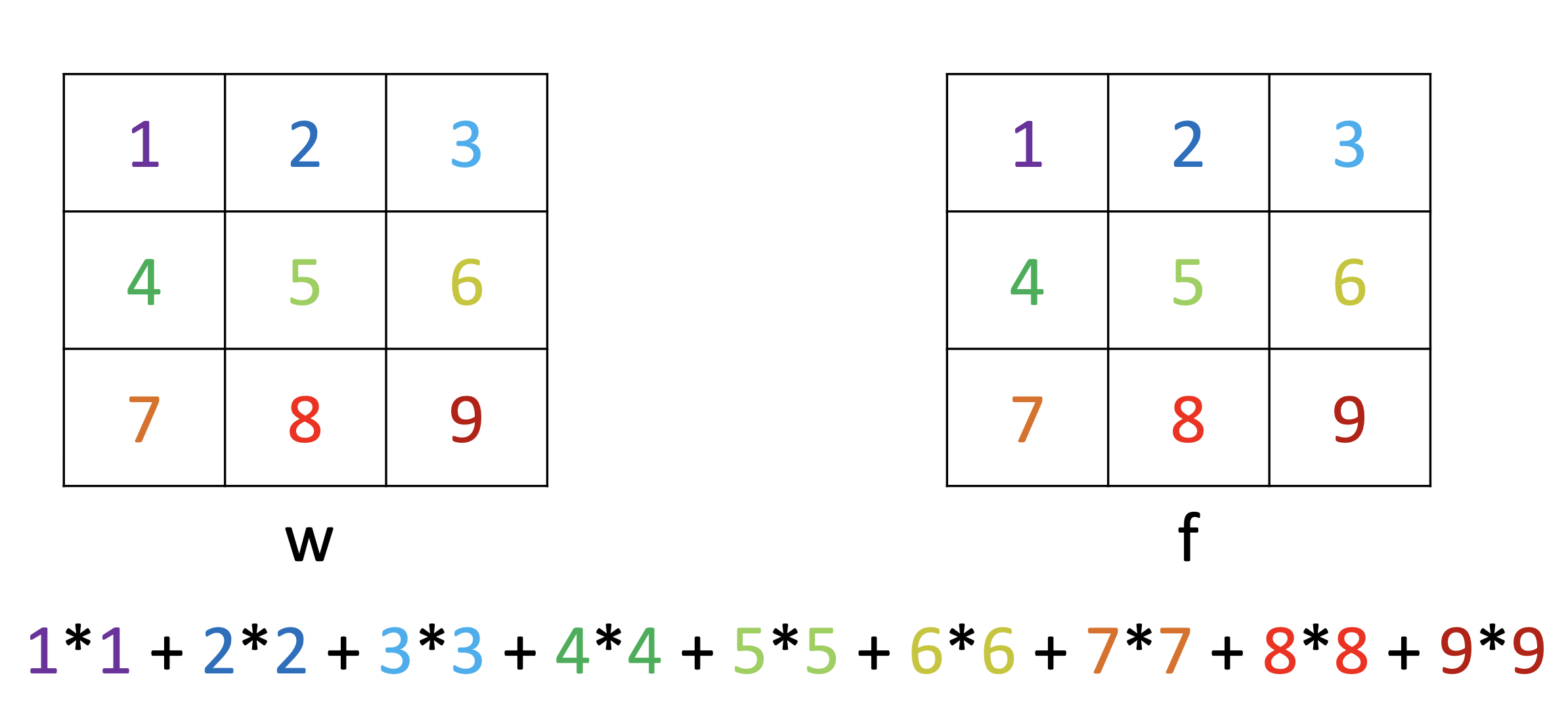
S[f]=w \otimes f=\sum_{i=-k}^{k}\sum_{j=-k}^{k}w(i,j)f(m+i,n+j)

위의 수식대로 연산을 진행하면 위와 같이 각 픽셀에 대응하는 순서대로 곱하고 모두 더하는 연산을 진행하게 됩니다.

Convolution

S[f] = w*f = \sum_{i=-k}^{k} \sum_{j=-k}^{k} w(i, j)f(m-i, n-j)

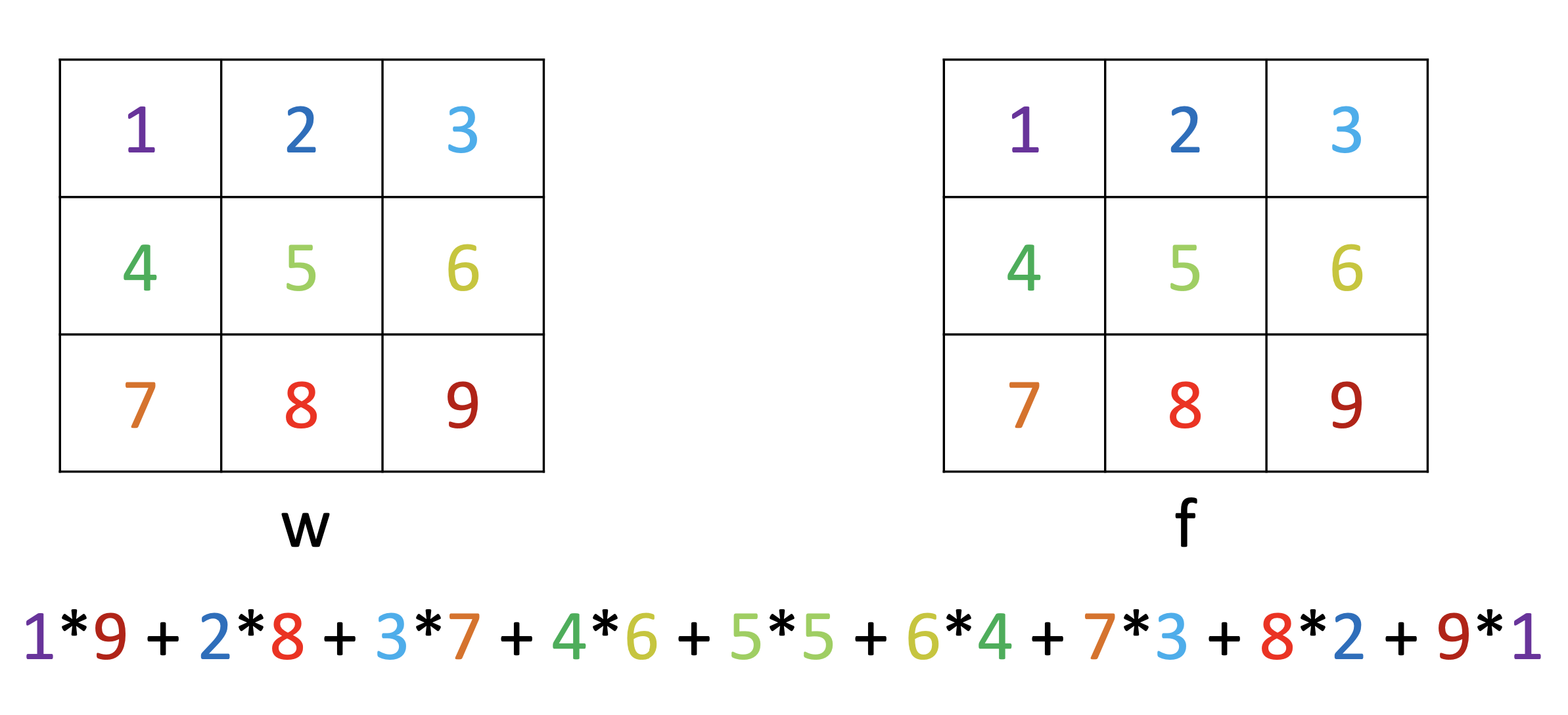
Cross-Correlation과 달리, Convolution은 각 픽셀에 대응하는 순서의 역방향으로 곱하고 모두 더하는 연산을 진행합니다.

즉, Cross-Correlation과 Convolution은 점들을 곱하는 순서가 정반대이고, 이것은 커널을 상하좌우로 반전한 것과 같습니다.

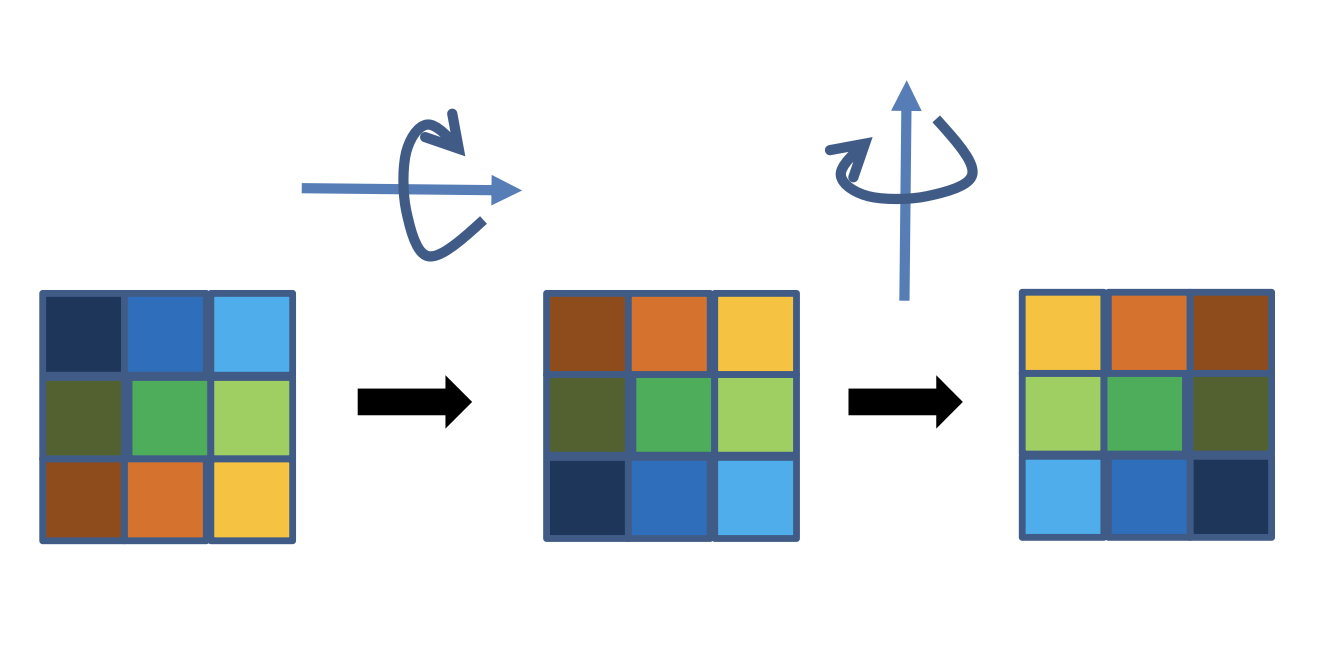
선형성(Linearity), 이동 불변성(Shift invariance)

위의 연산들은 다음과 같이 선형성과 이동 불변성의 특성을 가집니다.

선형성

f'(m,n) = af(m,n) \\ (w \otimes f')(m,n) = a(w \otimes f)(m,n)

f' = af+bg \\ w \otimes f' = a(w \otimes f)+b(w \otimes g)

w' = aw+bv \\ w' \otimes f = a(w \otimes f)+b(v \otimes f)

이동 불변성

f'(m,n) = f(m-m_{0},n-n_{0})

\begin{aligned} (w \otimes f')(m,n) &= \sum_{i=-k}^{k}\sum_{j=-k}^{k} w(i, j)f'(m+i,n+j) \\ &=\sum_{i=-k}^{k}\sum_{j=-k}^{k}w(i, j)f(m+i-m_{0},n+j-n_{0}) \\ &=(w \otimes f)(m-m_{0},n-n_{0}) \end{aligned}

이동 불변성은 이동한 다음 convolve한 것과, convolve한 다음 이동한 것은 같다는 성질입니다.

Convolution의 결과는 픽셀의 위치에 상관 없다는 것입니다.

구현 코드

파이썬으로 Convolution을 구현한 코드는 다음과 같습니다.

def convolve2d(array, filter):
    array_height, array_width = array.shape
    filter_size = len(filter)
    padding_size = math.ceil((filter_size - 1) / 2)

    filter = np.flip(filter) # Convolution 구현을 위해서 필터 상하좌우 반전

    output_height = array_height + 2 * padding_size - filter_size + 1
    output_width = array_width + 2 * padding_size - filter_size + 1

    array = np.pad(array, ((padding_size, padding_size), (padding_size, padding_size)), "constant", constant_values=0) # 패딩 적용
    output = np.ones((output_height, output_width), dtype=np.float32)

    # Convolution 연산 수행
    for y in range(output_height):
        for x in range(output_width):
            output[y][x] = np.sum(array[y:y+filter_size, x:x+filter_size] * filter)

    return output

이미지 배열 array와 필터 배열 filter을 인자로 입력 받습니다.

필터의 사이즈는 항상 홀수라고 가정합니다.

이미지 배열과 필터 배열의 사이즈를 구하고 패딩의 사이즈를 구합니다.

패딩은 입력 사이즈와 출력 사이즈를 동일하게 유지하기 위해서 적용해줍니다.

패딩의 사이즈는 $(kernel\,size-1)/2$ 로 구합니다.

Convolution과 Cross-Correlation은 커널이 상하좌우 반전된 차이가 있기 때문에 np.filp() 함수를 사용해서 커널을 뒤집어 줍니다.

np.pad() 함수를 사용해서 입력 이미지 배열에 패딩을 적용해주고 이중 반복문을 이용해서 각각의 대상 픽셀에서 Convolution 연산을 진행합니다.

wyj

다음 포스트