가우시안 필터 (Gaussian Filter)
평균 필터는 대상 점을 주변 픽셀들의 평균값으로 대체하기 때문에 이미지를 블러링(blurring)하는 효과를 가집니다.
평균 필터는 필터의 모든 값이 동일합니다.
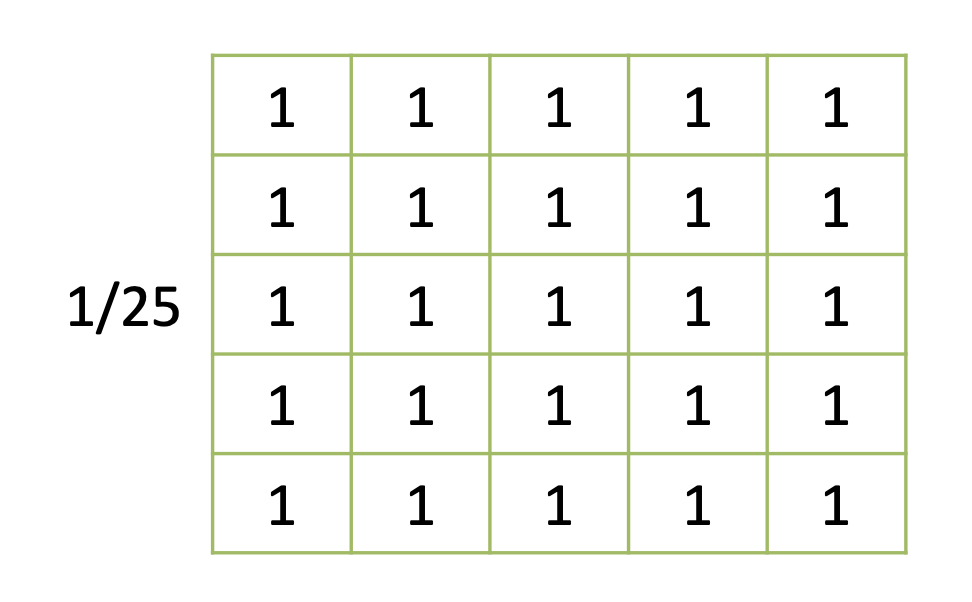
하지만 이러한 특성은 대상 점과 가까운 픽셀이 먼 픽셀보다 더 연관이 있다는 사실을 반영하지 못합니다.
가까운 픽셀에 더 많은 가중치를 줄 필요가 있습니다.
이러한 것을 반영하기 위해서 가우시안 필터를 사용할 수 있습니다.
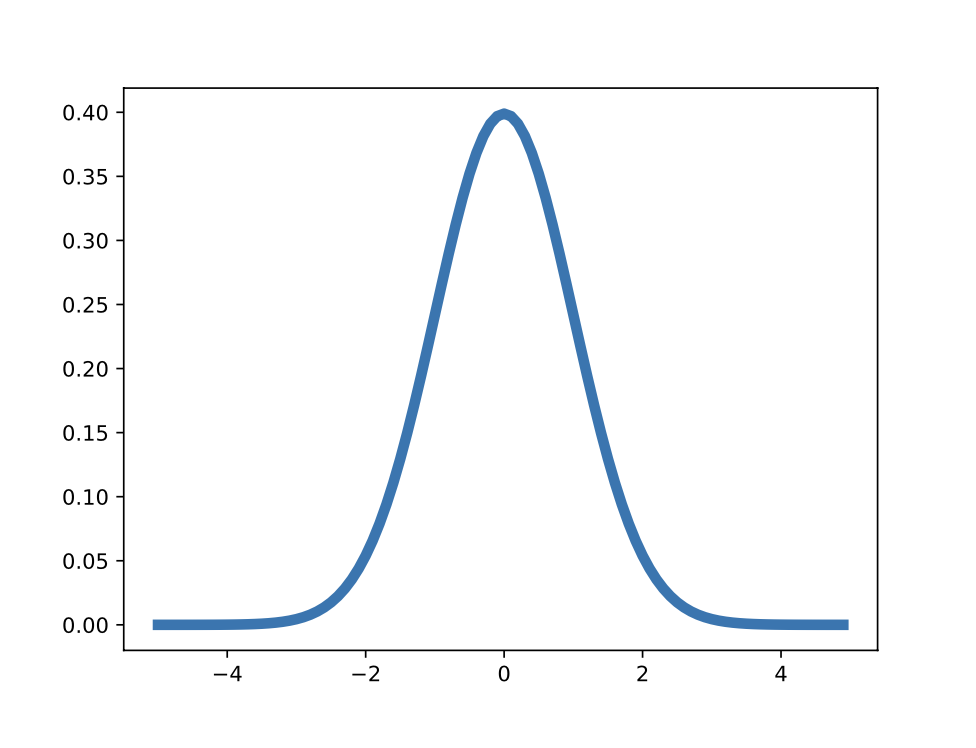
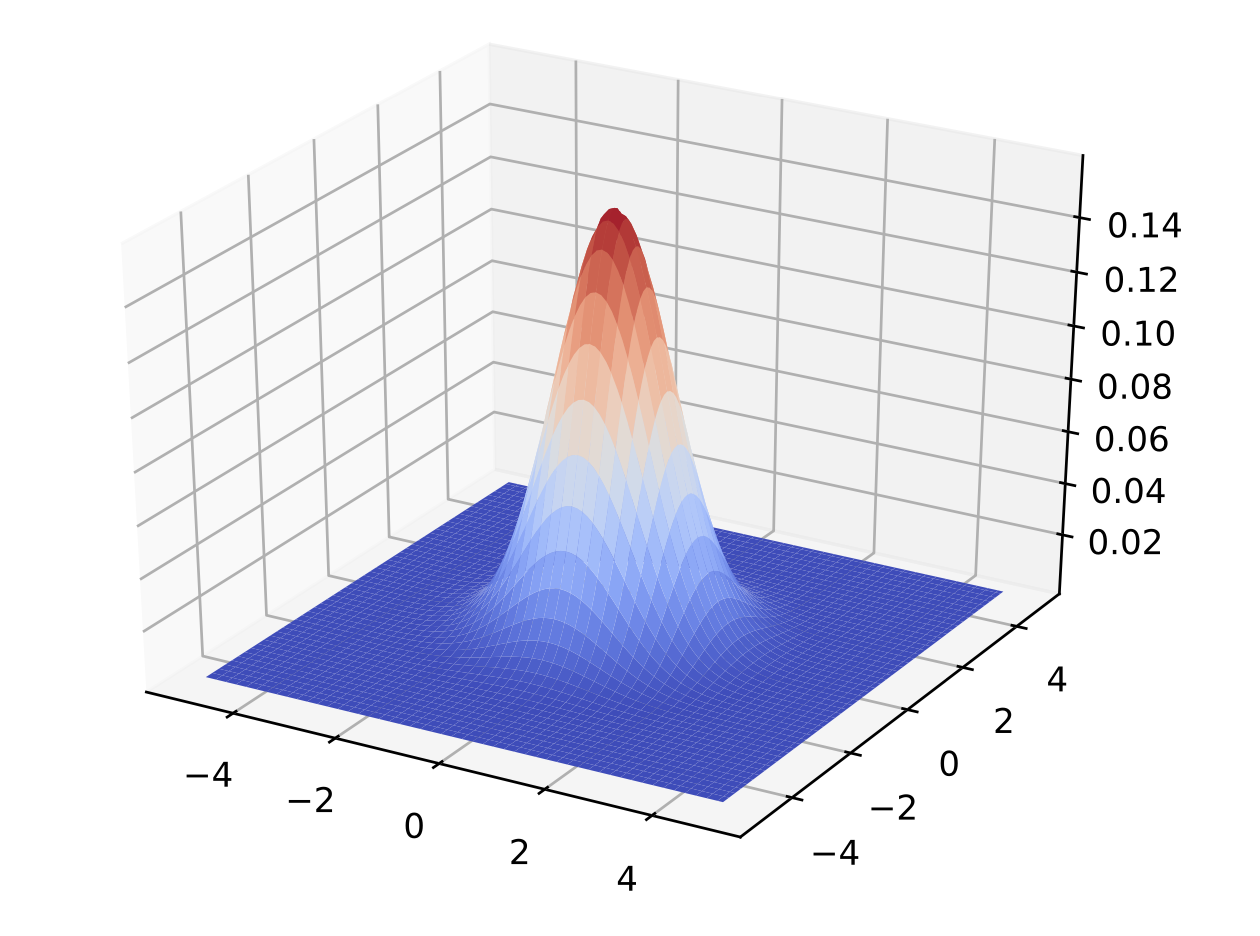
보시는 것 처럼 가우스 함수는 대상 점의 값이 가장 크고, 대상 점에서 멀어질수록 값이 작아지는 특징이 있습니다.
위의 식을 이용해서 커널은 만들면 가우시안 필터가 되는 것입니다.
가우시안 필터는 아래와 같습니다.
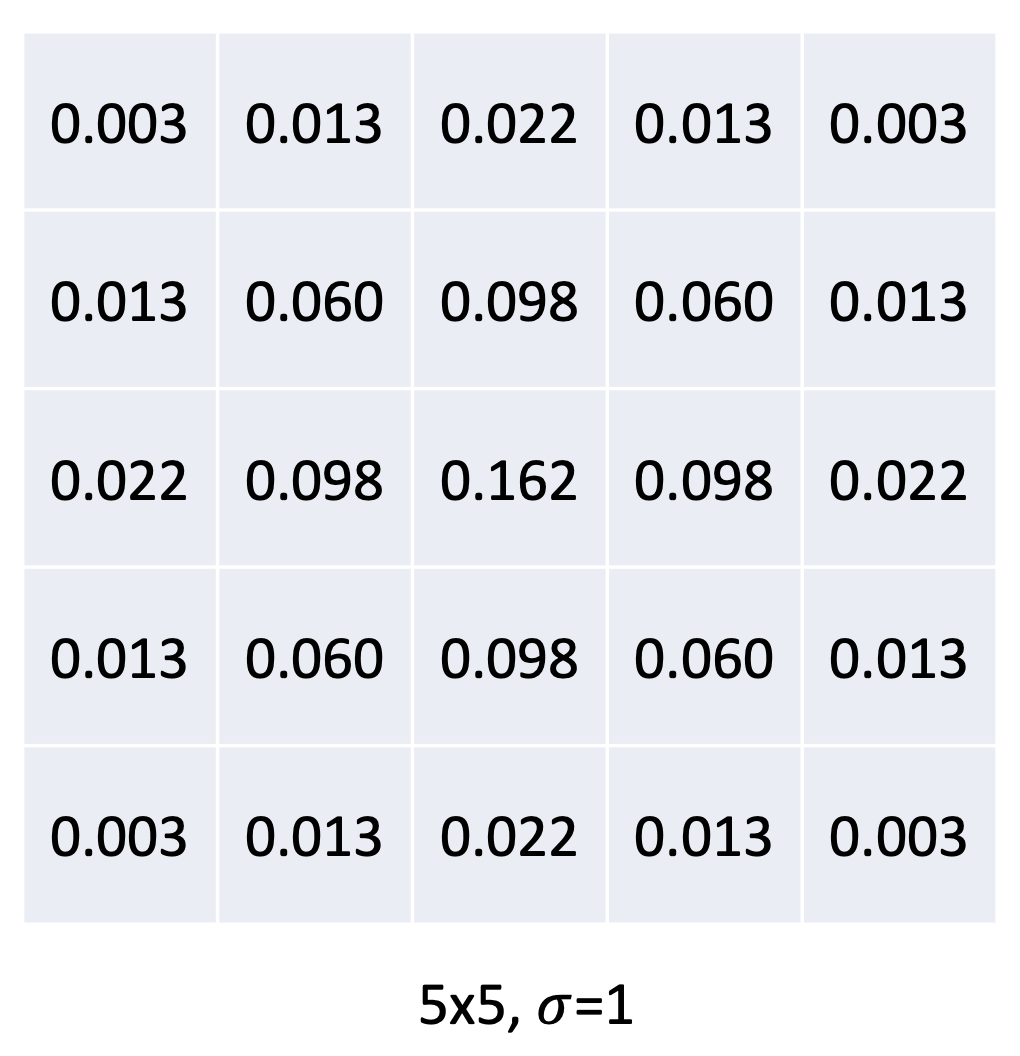
가우스 함수의 값은 표준편차를 나타냅니다.
표준편차의 값이 클 수록 분포는 완만해지고, 표준편차의 값이 작을수록 분포는 뾰족해집니다.
가우시안 필터의 값이 클 수록 대상 점에서 멀어질수록 값이 작아지는 정도가 크기 때문에 블러링 효과는 커집니다.
반대로 깂이 작을 수록 대상 점에서 멀어질수록 값이 작아지는 정도가 작기 때문에 블러링 효과는 작아집니다.

Low-pass Filter, High-pass Filter
가우시안 필터는 Low-pass Filter입니다.
Low-pass filter는 이미지로부터 "high-frequency"를 제거하는 필터입니다.
이미지에 가우시안 필터를 convolve하면 블러링된 이미지를 얻을 수 있습니다.
이때, 블러링된 이미지를 원래 이미지에서 빼면 이미지의 디테일한 부분을 얻을 수 있습니다.

이렇게 이미지의 디테일한 부분을 추출하는 연산을 High-pass Filter라고 합니다.
Sharpening
원본 이미지에서 블러링된 이미지를 빼면 디테일한 부분을 얻을 수 있습니다.
원본 이미지에서 디테일한 부분을 더하면 더욱 선명한 이미지를 얻을 수 있습니다.

구현 코드
파이썬으로 가우시안 필터를 구현한 코드는 다음과 같습니다.
먼저, 1차원 가우시안 필터를 구현한 코드입니다.
def gauss1d(sigma):
length = math.ceil(sigma * 6)
if length % 2 == 0: length += 1
kernel = np.arange(-(length // 2), (length // 2) + 1, dtype=np.float32)
kernel = np.vectorize(lambda x: np.exp(-(x ** 2) / (2 * sigma ** 2)))(kernel)
kernel = kernel / np.sum(kernel)
return kernel가우시안 필터의 사이즈는 를 6배한 값보다 큰 최소의 홀수입니다.
각 원소의 값은 중앙으로부터의 거리 값입니다.
numpy 배열을 준비한 다음, 각 원소에 가우시안 함수를 적용해 줍니다.
모든 원소의 합은 1이 되도록 정규화해주는 과정도 필요합니다.
다음으로, 2차원 가우시안 필터를 구현한 코드입니다.
def gauss2d(sigma):
kernel1d = gauss1d(sigma)
kernel2d = np.outer(kernel1d, kernel1d.T)
kernel2d = kernel2d / np.sum(kernel2d)
return kernel2d2차원 가우시안 필터는 1차원 가우시안 필터를 외적해서 구할 수 있습니다.
마찬가지로 모든 원소의 합을 1이 되도록 정규화 해줍니다.