이 글은 스탠포드 대학의 CS224W(2020) 강의를 듣고 정리한 글입니다.
뒤에서 다룰 Graph를 활용한 Machine Learning 기법들을 소개하기 앞서,
Graph를 활용하기 위해 기본적으로 알아야하는 구조와 다양한 표현방식에 대해 먼저 다루고자 한다.
1. Graph
먼저 Graph의 구조와 이 구조가 가지는 특징에 대해 살펴보자.
Components
Graph는 ① Nodes ② Edges 로 구성되어 있으며, 이것들로 이루어진 것을 ③ Graph라고 한다.
이는 각각 다른 단어로 표현되기도 하고, 특정 용어로 표현되기도 하니 아래를 참고하자.
- 정점(Nodes, Vertices) : 특정 객체(Objects)를 의미하며, 주로 으로 표기
- 간선(Edges, Links) : Node 사이의 상호작용(Interactions)을 의미하며, 주로 으로 표기
- 그래프(Graph, Network) : 객체 간의 상호작용으로 이루어진 System을 의미하며, 으로 표기
Directed vs Undirected
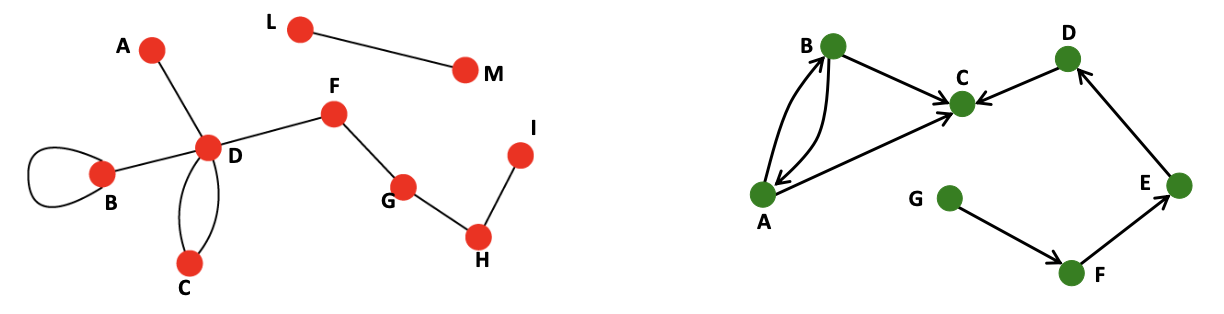
위의 그림에서 좌측이 Undirected, 우측이 Directed Graph 이다.
사전에 정의 된 객체 간의 상호작용이 쌍방으로 이뤄진다면 Undircted Graph,
그렇지 않고 상호작용이 일방적인 형태라면 Directed Graph를 선정하는 것이 일반적이다.
Node Degrees
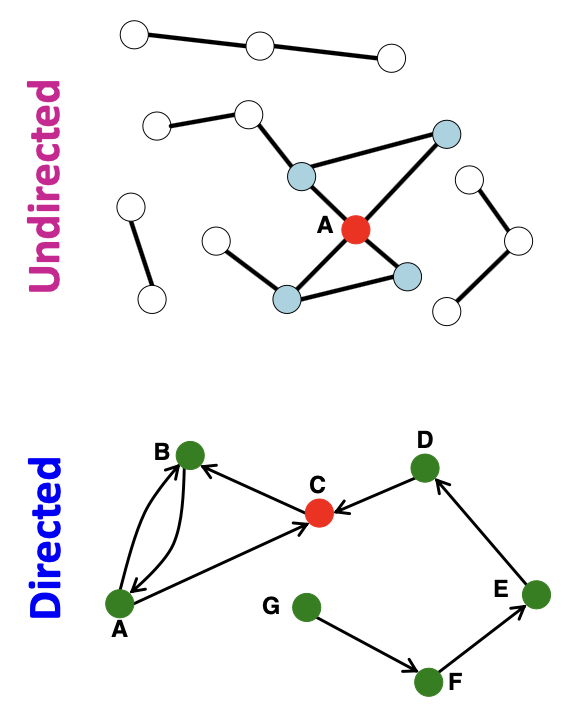
Node Degress는 1개의 Node와 연결되어 있는 Edge의 개수를 의미하며,
Node 의 Degree는 , 전체 Graph의 평균 Degree는 와 같이 표기할 수 있다.
다만 아래와 같이 Undirected / Directed Graph 여부에 따라 각각의 계산 방식은 조금 달라질 수 있다.
- Node degree in Undirected Graph
- Node A Degree = = 4 (Edge 개수)
- Node A Avg. Degree = = =
- Node degree in Directed Graph
- Node C In-Degree = = 2 (In-Edge 개수)
Node C Out-Degree = = 1 (Out-Edge 개수) - Node C Avg. Degree = =
- Node C In-Degree = = 2 (In-Edge 개수)
Bipartite Graph
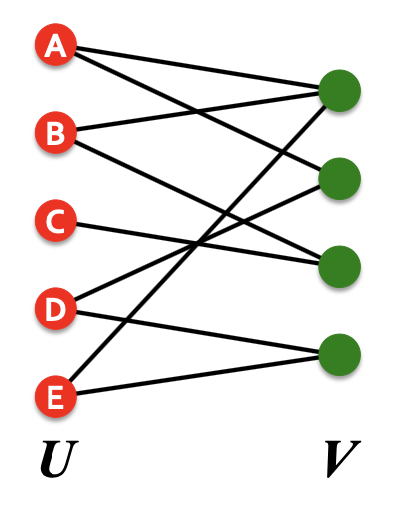
이분 그래프(Bipartite Graph)는, 1개의 Graph를 서로소인 2개의 Node 집합으로 나눌 수 있는 Graph를 의미한다.
이때 나누어진 Node 집합 에서, 의 모든 Node와 연결된 Edge는 모두 와 연결되어야 한다.
(이는 , 가 서로 독립임을 의미한다.)
이러한 특징을 가진 이분 그래프는, 서로 특징이 다른 2개 집합 간의 상호작용을 표현할때 나타내며
작가-저서, 배우-영화, 관객-영화 등과 같은 관계에 사용된다.
2. Graph Representation
주어진 도메인/문제에 적합한 Graph의 표현 방식을 선정하는 것은 데이터를 보다 더 잘 설명하고 모델의 성능을 더 높이기 위해서 중요한 일이라고 말할 수 있다.
그럼 Graph의 표현 방식에는 어떤 것이 있는지 살펴보자.
Adjacency Matrix
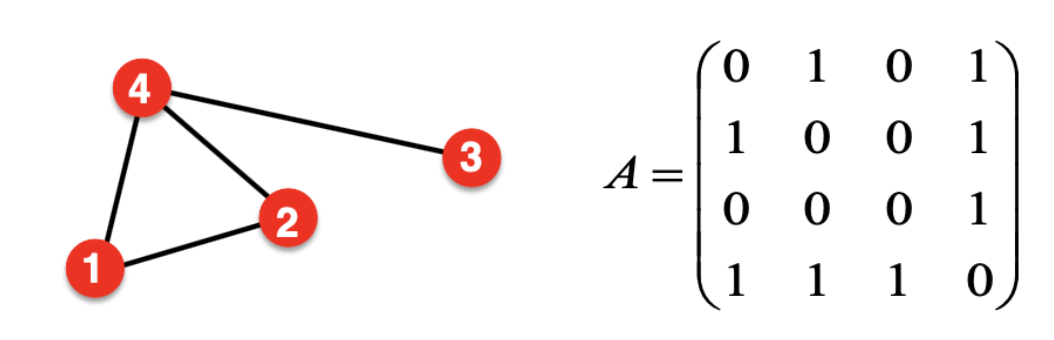
Edge List
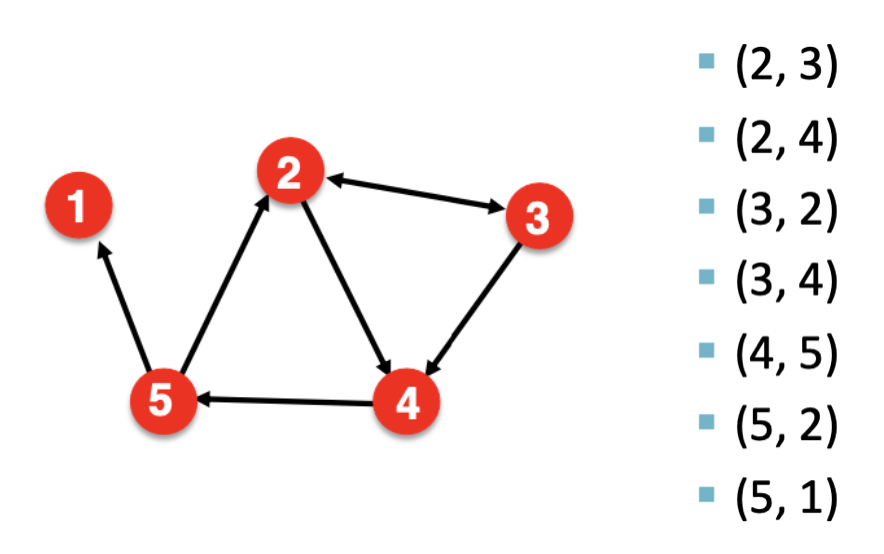
다만 각각의 Edge를 Tuple 형태로 표현하기 때문에, 데이터를 분석하거나 가공하기 어렵다는 단점이 있다.
Adjacency List
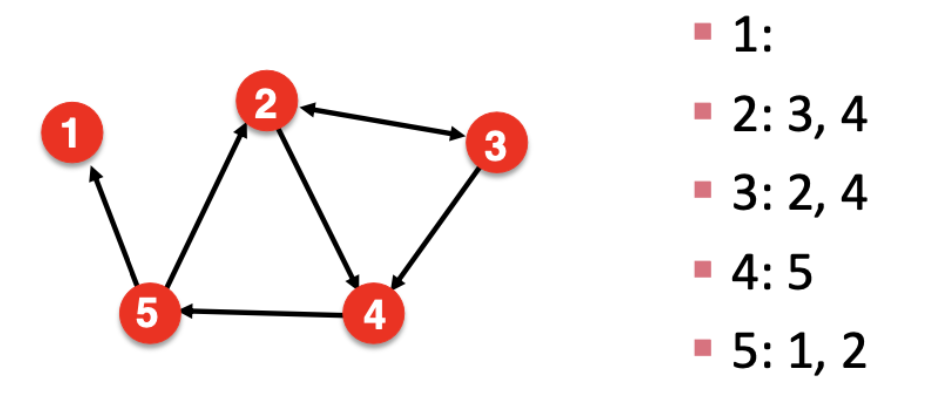
앞서 언급한 Adjacency Matrix와 Edge List가 갖는 단점을 보완한 것이 바로 Adjacency List 이다.
Adjacency List는 각 Node가 Key이고, 해당 Node와 연결되어있는 다른 Node를 Value로 가지는 Key-Value 구조이다.
해당 구조를 활용한 Adjacency List는 주어진 Node에 대한 근접 Node들을 빠른 시간 내에 찾을 수 있다.
More Types of Graphs
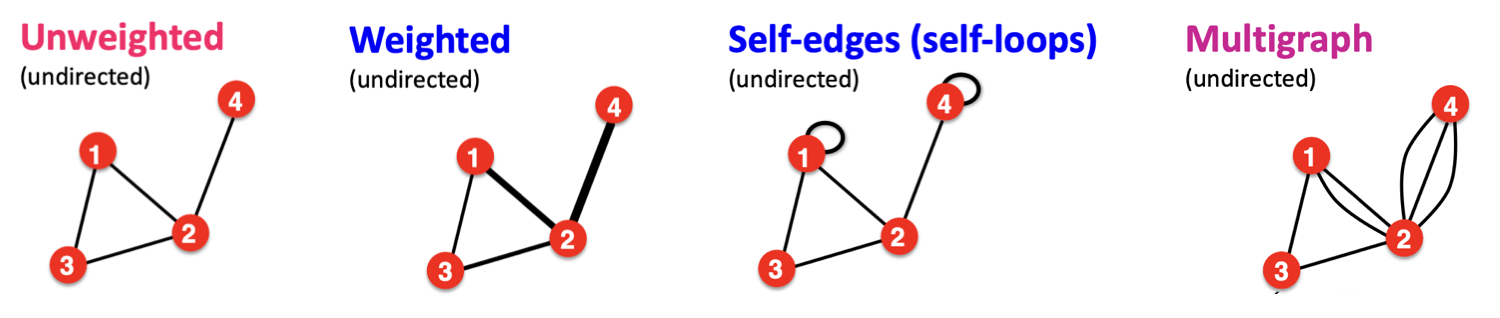
3. Connectivity
연결성(Connectivity)은, Graph의 Node들이 서로 얼마나 잘 연결되어 있는지를 나타내는 개념이다. 이는 Undirected, Directed Graph에서 다르게 정의될 수 있다.
- Undirected Graph
- Connected Graph : 모든 Node 쌍에 하나의 경로라도 존재하는 경우
- Disonnected Graph : 모든 Node 쌍에 하나의 경로라도 존재하지 않는 경우
- Directed Graph
- Strongly : 모든 Node 쌍 v, m에 대한 경로가 존재
- Weakly : Strongly에 해당 되지 않는 경우
- SCSs(Strongly connected components)
: 주어진 Graph에서 모든 Node가 아닌 일부 Node의 집합에 대해서 Node 쌍에 대한 Strongly Connected가 되는 경우, 해당 Node 집합을 SCSs라고 말한다.