CS224W #2 Traditional Methods for ML in Graphs

Kyeongmin·2025년 1월 25일
0

인공지능

목록 보기
4/9

이 글은 스탠포드 대학의 CS224W(2020) 강의를 듣고 정리한 글입니다.

이번 글에서는 Graph 구조를 가진 데이터를 처리하기 위한 전통적인 ML 방법론에 대해 살펴볼 것이다.

Graph ML을 통해 수행하려는 Task의 유형들과, 각각의 Task에서 사용하는 Feature의 종류에 대해 다뤄보고자 하며, 이를 Graph의 3가지 구성요소(Node/Edge/Graph)를 기준으로 구분하여 설명하고자 한다.

1. Node-Level

만약 우리가 Node Classification을 하려면, 각각의 Node에 대한 특징을 알아야 할 것이다.
예로는 전체 Graph 내에서 Node의 위치 등과 같은 특징이 있을 것이며, Feature는 이러한 특징을 잘 나타낼 수 있어야한다. 다음 내용에서 Feature로 주로 사용되는 항목들을 살펴보고자 한다.

1) Node Degree

먼저 가장 간단한 Node의 특징 중 하나인 Node Degree는,
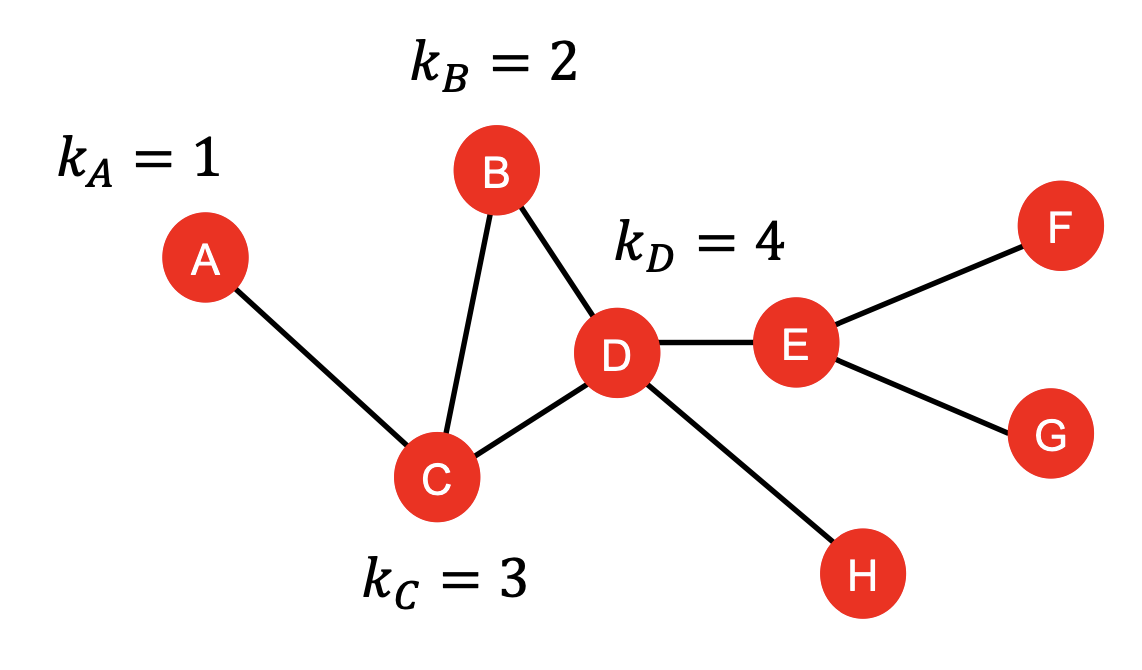
아래 그림과 같이 Node와 연결되어 있는 Edge(≈Node)의 개수를 의미한다.

다만 Node Degree는, 이웃한 Node의 Importance는 고려하지 않는다는 문제점이 있다.

2) Node Centrality

Node Centrality는 Node의 Importance를 고려하는 특징이다.
어떤 기준을 통해 Importance를 측정하냐에 따라 여러 방안이 있으며, 여기서는 3가지 방안을 소개하고자 한다.

① Eigenvector centrality
Eigenvector centrality는, 주변 Node의 Importance를 통해 현재 Node의 Importance를 측정하는 방법이다.

이를 수식으로 표현한 것이 아래의 식인데,
이웃 Node의 centrality cuc_u 의 합을 상수 λ\lambda로 나눈 값을 특정 Node의 Centrality cvc_v 임을 의미한다.

cv=1λ∑u∈N(v)cuc_v = \frac{1}{\lambda}\sum_{u \in N(v)} c_u

이러한 식을 행렬 형태로 표현한다면, Eigenvalue 문제와 같게 된다.
이를 해석하자면 인접 행렬 A{A}에 대한 Eigenvalue(고유값)이 우리가 찾고자 하는 λ\lambda이며,
Graph의 Centrality Vector cc는 Eigenvector(고유벡터)가 됨을 알 수 있다.

λc  =  Ac\lambda c \;=\; Ac

② Betweenness centrality
Betweenness centrality는, 다른 Node 쌍의 최단 경로에 특정 Node가 얼마나 포함되어 있는지를 나타내는 값이다.

cv=∑s≠v≠tσs,t(v)σs,tc_{v} = \sum_{s \neq v \neq t}\frac{\sigma_{s,t}(v)}{\sigma_{s,t}}

여기서 σs,t\sigma_{s,t} 는 Node s,ts, t 간의 최단 경로의 수를 의미하며
σs,t(v)\sigma_{s,t}(v) 는 Node s,ts, t 간의 최단 경로에 Node vv 를 포함하는 경로의 수를 의미한다.
이는 다른 Node 간의 Bridge 역할을 많이 하는 Node 일수록 중요한 Node라고 간주하는 방식이다.

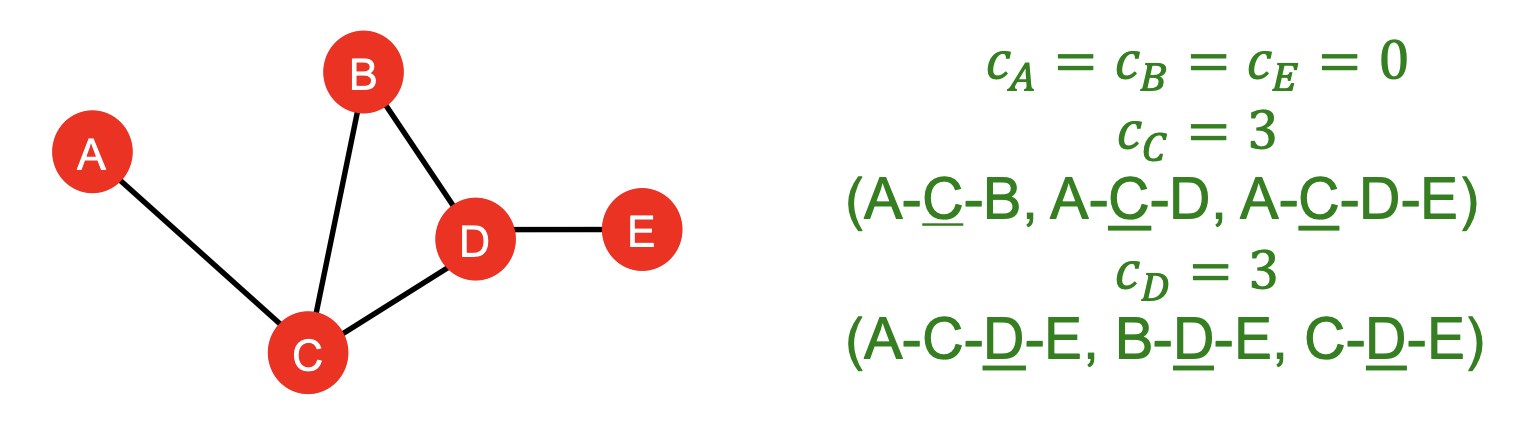
위의 예시와 같이, Node의 끝부분에 위치한 Node A,B,CA,B,C는 다른 Node 간의 최단 경로에 포함되지 않기 때문에 Centrality = 0 임을 확인할 수 있다.

③ Closeness centrality
Closeness centrality는, 특정 Node와 다른 Node 까지 도달하는 최단 경로 길이의 합을 나타내며,
다시 말해 다른 모든 Node와의 근접도를 나타내는 값이다.

cv=1∑u≠vd(u,v)c_{v} = \frac{1}{\sum_{u \neq v} d(u,v)}

Betweenness centrality 와는 달리 실제 최단 경로의 거리값을 사용하며,
아래는 Closeness centrality의 예시이다.

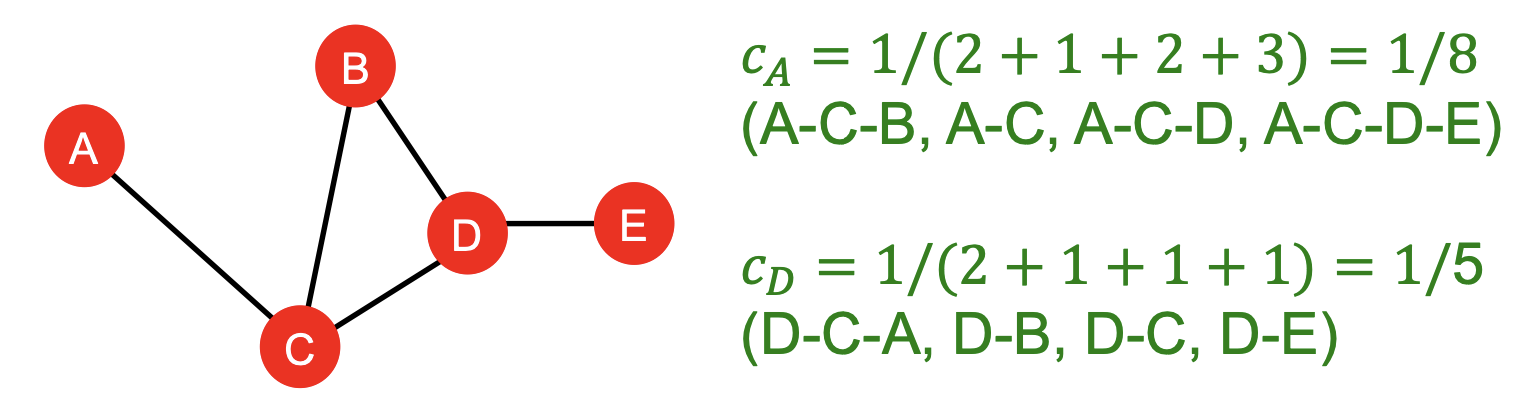
3) Clustering coefficient

Clustering coefficient는 특정 Node를 중심으로 해당 Node의 이웃 Node들이 얼마나 서로 잘 연결되어 있는지를 측정하는 지표이며, 이를 통해 Local Connectiviy를 파악할 수 있다는 장점이 있다.

특정 Node vv가 있을 때, 이웃 Node 들끼리 모두 연결되어 있다면(≈이웃들끼리 완전 그래프를 이루면)
값이 1이 되고, 이웃 Node 들 사이의 연결이 전혀 없다면 0이 된다.

이를 수식으로 표현하면 아래와 같고, 분자는 이웃 Node 간 실제 연결된 Edge 수를 의미하며
분모는 이웃 Node 간 연결될 수 있는 모든 Edge 수를 의미한다.

ev=#(edges among neighboring nodes)(kv2)e_v = \frac{\#(\text{edges among neighboring nodes})}{\binom{k_{v}}{2}}

아래는 Clustering coefficient에 대한 예시이며,
첫번째 그림 같은 경우 이웃 Node 간에 모두 연결 되어 있기 때문에 ev=1e_v=1 이다.

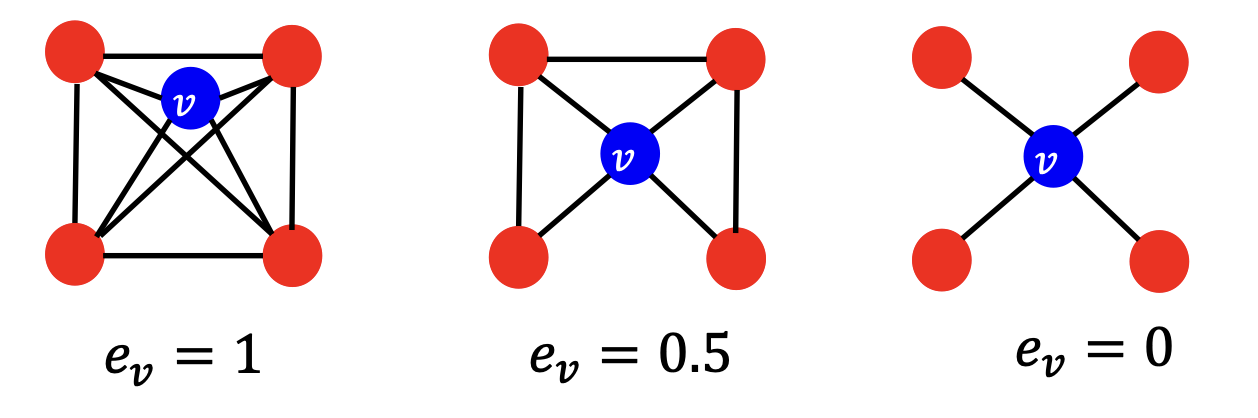
4) Graphlets

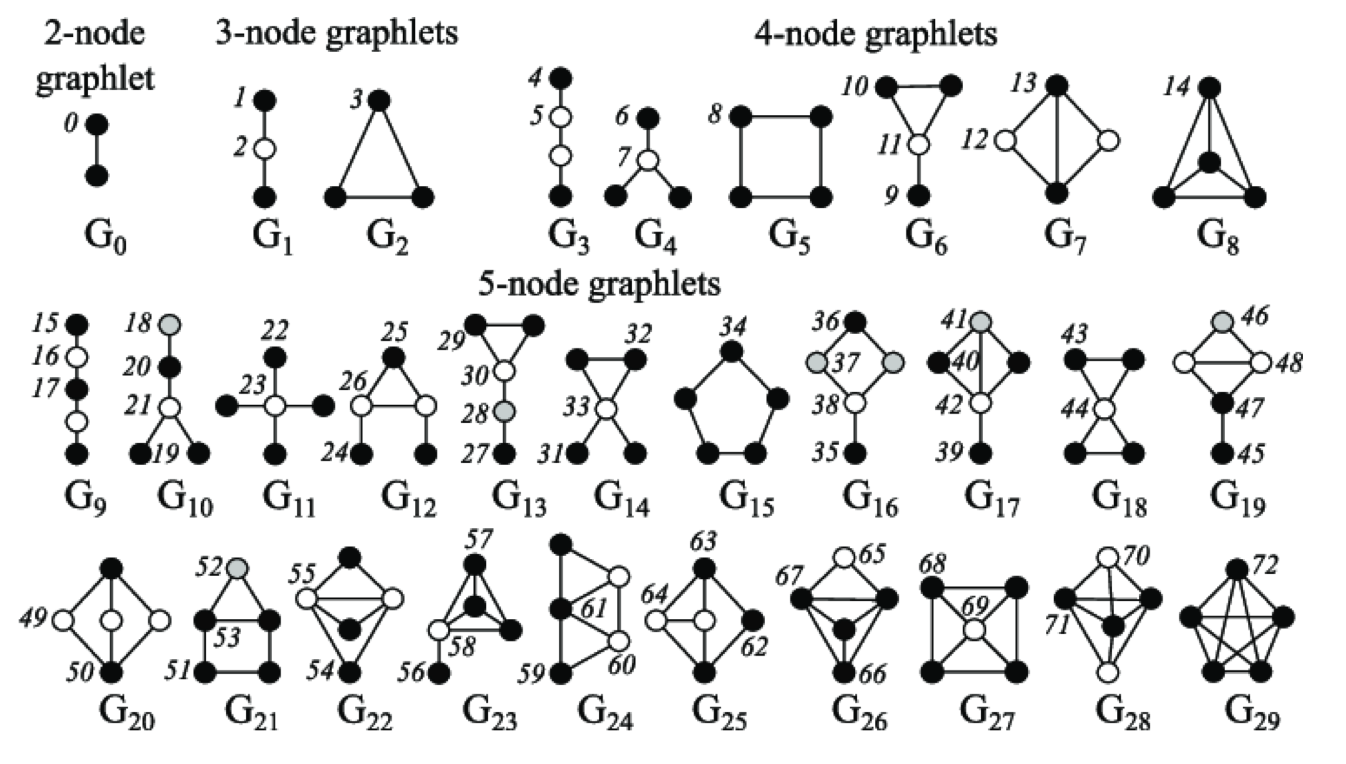
Graphlets란 그래프의 연결된 작은 부분 Graph(subgraph) 중에서,
서로 동형(isomorphic)이지 않은 고유한 형태들만 모아 놓은 일종의 ‘Graph Pattern’ 집합이다.

아래 그림을 살펴보면, Graph Pattern 내에 숫자가 존재하는데,
이는 Subgraph의 고유한 형태를 만들기 위한 Root(특정 Node)를 의미한다.

위에서 다룬 4가지 항목들은 아래와 같이 2개 유형으로 분류할 수 있다.

  • Important-based
    • 전체 Graph에서 특정 Node의 중요성을 나타내는 특징
    • Node degree, Node Centrality
  • Structure-based
    • 전체 Graph 내의 부분적인 구조적 속성을 나타내는 특징
    • Node degree, Clustering coefficient, Graplets

Link-Level Feature는 기존 Link(=Edge)에 기반하여 새로운 Link를 예측하기 위해 사용되며, 일반적으로 Node 쌍에 대한 정보를 담고 있다.

1) Distance-based

가장 간단한 방법으로, 2개 Node 간의 최단 거리를 사용하는 방안이다.

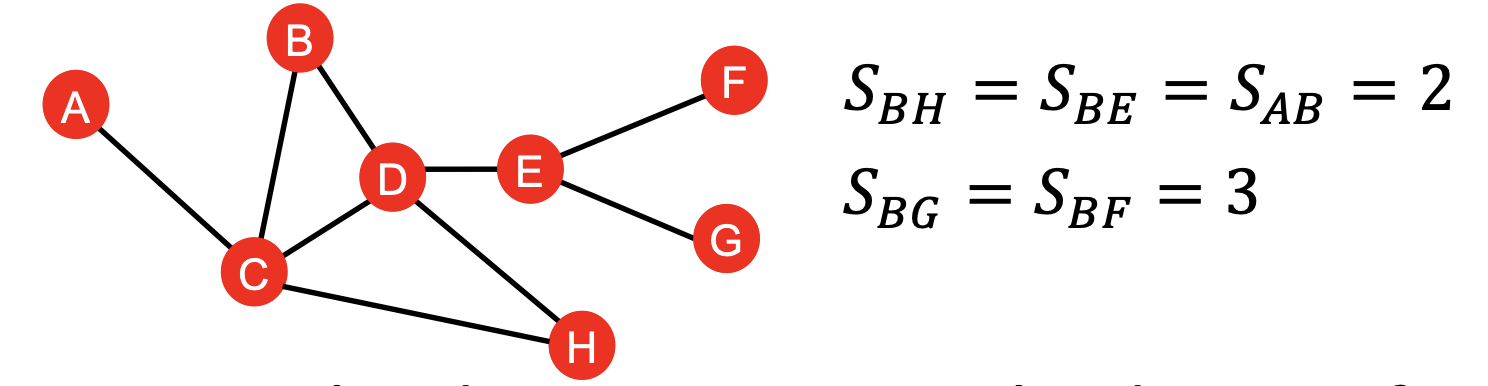
다만 이러한 방식은 아래 그림과 같이,
Node(B,H)는 최단 경로가 2개이고 Node(A,B)는 최단 경로가 1개이나
이러한 점을 고려하지 못하고 동일한 값(SBH=SAB=2S_{BH} = S_{AB} = 2)을 가진다는 단점이 있다.

2) Local neighborhood overlap

Local neighborhood overlap은 Distance-based Metric과 달리 주변 Node와의 관계를 고려하며,
2개 Node 간에 얼마나 많은 이웃 Node를 공유하는지를 측정하는데에 중점을 둔 지표이다.

아래와 같이 여러 Metric이 존재하며, 대체로 간단한 편이어서 수식만 기술하였다.

① Common neighbors

∣N(v1)∩N(v2)∣|N(v_1) \cap N(v_2)|

② Jaccard's coefficient

∣N(v1)∩N(v2)∣∣N(v1)∪N(v2)∣\frac{|N(v_1) \cap N(v_2)|}{|N(v_1) \cup N(v_2)|}

③ Adamic-Adar index

∑u∈N(v1) ∩ N(v2)1log⁡(ku)\sum_{u \in N(v_1)\,\cap\,N(v_2)} \frac{1}{\log\bigl(k_u\bigr)}

단점
다만 이러한 지표의 단점으로는, 아래 그림과 같이 직접 연결된 이웃 Node가 아니라면 무시된다.

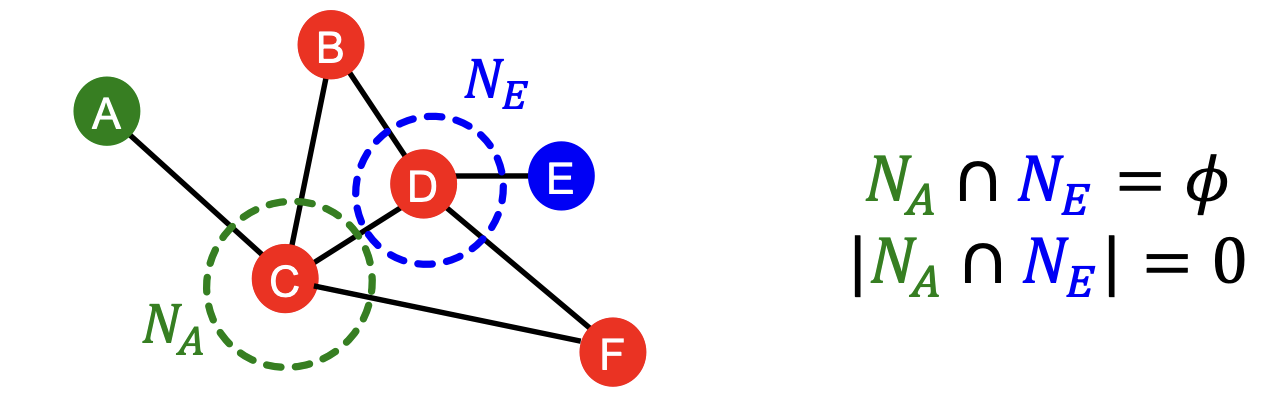
3) Global neighborhood overlap

Global neighborhood overlap은 전체 Graph를 고려함으로써 앞서 언급한 단점을 보완하는 방안으로, 주로 Katz Index를 활용한다.

Katz Index는 Graph 내의 모든 경로를 고려하되,
짧은 경로는 큰 가중치, 먼 경로는 작은 가중치를 부여하여 2개 Node 간의 연결 강도를 측정하는 방식이다.

수식은 아래와 같고, 모든 경로를 고려하기 위해 인접행렬 AA를 사용하는 것을 알 수 있다.

Sv1v2=∑l=1∞βl A v1v2l(where 0<β<1),S=∑i=1∞βi Ai=(I−βA)−1  −  I\begin{aligned} S_{v_{1}v_{2}} &= \sum_{l=1}^{\infty} \beta^{l}\,A^{l}_{\,v_{1}v_{2}} \quad\text{(where }0 < \beta < 1\text{),} \\ S &= \sum_{i=1}^{\infty} \beta^{i}\,A^{i} \\ &= (I - \beta A)^{-1} \;-\; I \end{aligned}

Av1v22A_{v_{1}v_{2}}^2는 Node v1,v2v_1,v_2 사이의 거리가 2인 경로이며, 제곱의 수는 Node 간의 거리를 의미하는데
거리가 멀어질수록 β\beta를 통해 작은 가중치를 부여하는 것을 알 수 있다.

3. Graph-Level

Graph-Level에서의 Feature는, 전체 Graph의 구조 및 특징을 나타내야 한다.
여기에서는 Feature 대신 Kernel을 활용하며 Graph Kernel / WL Kernel 등이 존재한다.

Kernel

먼저 Kernel에 대해 잠깐 리마인드 하고 넘어가자.
Kernel은 2개의 데이터가 주어졌을때 유사도를 측정하는 함수이며, ML에서 학습을 위해 사용되는 Feature Vector를 만들어내는 것이 아닌 이를 대신하는 Kernel을 설계하는 방법이다.

적절하게 설계 된 Kernel KK는, 아래와 같이 Feature Vector ϕ(⋅)\phi(\cdot) 형태로도 해석할 수 있는데,
이는 Feature Vector를 직접 만들지 않고도 Kernel을 통해 간접적으로 만들어 낼 수 있음을 의미한다.

K(G,G′)∈RK(G,G′)=ϕ(G)T⋅ϕ(G′)\begin{aligned} K(G, G^\prime) &\in \mathbb{R} \\ K(G, G^\prime) &= \phi(G)^{\text{T}} \cdot \phi(G^\prime) \end{aligned}

1) Graph Kernel

Graph 데이터에서는 위에서 볼 수 있었던 Graph Feature Vector ϕ(G)\phi(G)를 설계하는데 중점을 두며,
기본적으로 Bag-of-Words 방법을 활용하여 Feature를 설계하는 방식을 사용한다.

Bag-of-Words
어떠한 문장이 주어졌을때, 단어의 순서를 고려하지 않고 단어의 개수만 고려하는 방법

다만 단순히 Node Count를 사용하여 Feature를 설계한다면,
아래 그림과 같이 동일한 개수의 Node를 가지지만 다른 구조를 가진 Graph를 구별할 수 없다는 문제가 있다.

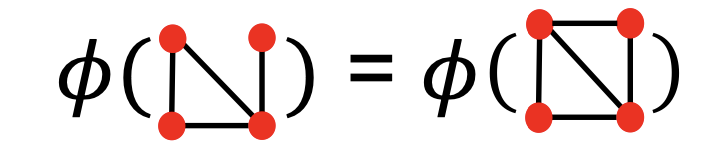
이를 해결하기 위해 Node Degree를 활용하는 방안이 제안되었으며,
동일한 개수의 Node를 가지더라도 다른 구조를 가진 Graph를 구별할 수 있다.

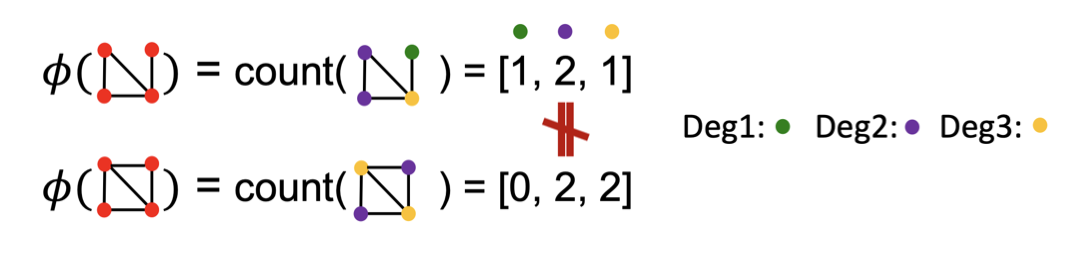
이렇게 어떤 특징을 사용하냐에 따라 Graph의 표현이 달라질 수 있다는 것을 알 수 있다.
이후에 소개할 Graphlet Kernel, Weisfeiler-Lehman Kernel에서는 동일한 Bag-of-Words를 통해 Feature를 설계하며, 이때 다른 특징을 사용하는 Bag-of-* 방식을 사용한다.

2) Graphlet Kernel

Graphlet Kernel은 말 그대로, Graphlet을 특징으로 사용한다.
다만 여기에서 다룰 Graphlet은 Node-Level Feature에서 다뤘던 Graphlet과 약간의 차이가 있다.

  • Node 간에 연결 되지 않아도 Graphlet의 구성요소로 볼 수 있다.
  • Root Node가 아니더라도 Graphlet의 구성요소로 볼 수 있다.

Graphlet을 활용한 Feature Vector fGf_{G}와 kernel KK는 아래와 같이 계산할 수 있다.
※ graph  G  ,  graphlet list  gk=(g1, g2, … gnk)\text{graph}\;G \;,\; \text{graphlet list}\;g_k=(g_1,\,g_2,\,\dots\,g_{n_k})

(fG)i=#(gi⊆G)fori=1, 2, …, nkK(G,G′)=fGT⋅fG′\begin{aligned} (f_G)_i &= \#\bigl(g_i \subseteq G\bigr) \quad\text{for}\quad i = 1,\,2,\,\dots,\,n_k \\ K(G, G^\prime) &= f_G^{\text{T}} \cdot f_{G^\prime} \end{aligned}

여기서 2개의 Graph(GG, G′G^\prime)가 다른 크기를 가질 수 있으므로,
아래와 같이 각 Vector의 크기로 정규화한 값을 사용하여 Kernel의 값이 한쪽으로 치우치지 않게 한다.

hG=fGSum(fG)andK(G,G′)=hGT hG′h_G = \frac{f_G}{\mathrm{Sum}(f_G)} \quad\text{and}\quad K(G,G') = h_G^{\text{T}}\,h_{G^\prime}

Graphlet Kernel의 단점
다만 Graphlet의 개수를 세는 작업은 비용이 지수함수적으로 증가하는 굉장히 큰 작업이다.

Graph 크기가 nn일때, Size-kk Graphlet을 세는 작업의 시간 복잡도는 nkn^k이며,
Graph 내의 Node Degree가 dd 이내라고 하더라도 시간 복잡도는 O(ndk−1)O(nd^{k-1}) 이다.

따라서 현실적으로 보다 효율적인 Kernel이 필요하였으며, 이를 위한 방법들이 뒤따라 제안되었다.

3) Weisfeiler-Lehman Kernel

보다 효율적인 Kernel 중 하나가 바로 Weisfeiler-Lehman Kernel(이하 WL Kernel) 이다.
이는 계산량이 많은 Graphlet이 아닌 Node degree + 1-hop neighborhood 정보를 활용한 방법이다.

WL Kernel을 설계하기 위한 알고리즘을 Color refinement 라고 하며, 아래의 4단계로 진행된다.

① 각각의 Node에 초기 색상(값) 설정

② 1-Hop neighborhood Node의 색상 취합

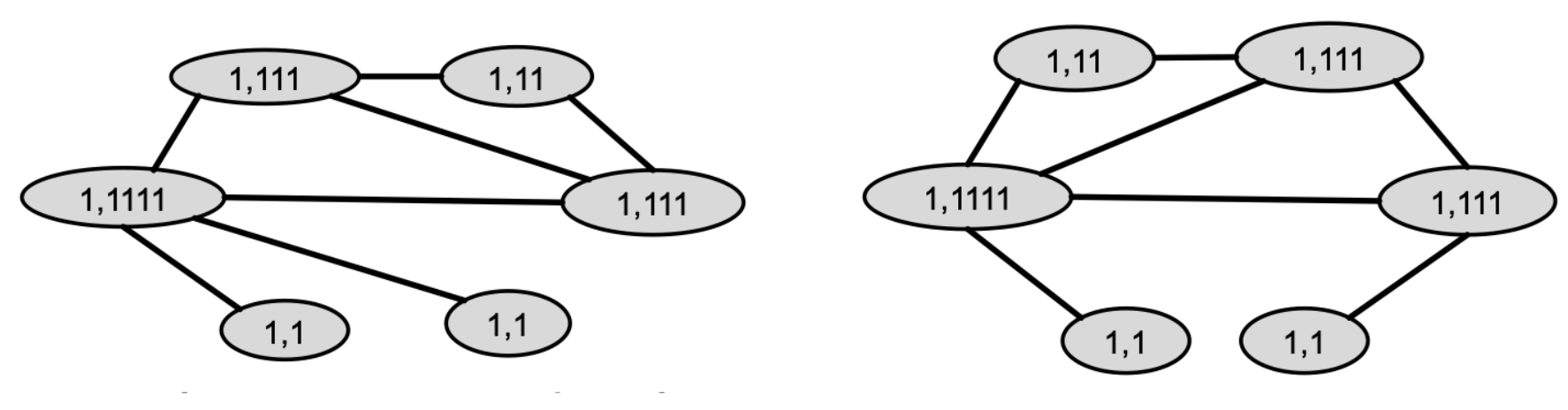
③ HASH 함수를 사용한 색상 업데이트

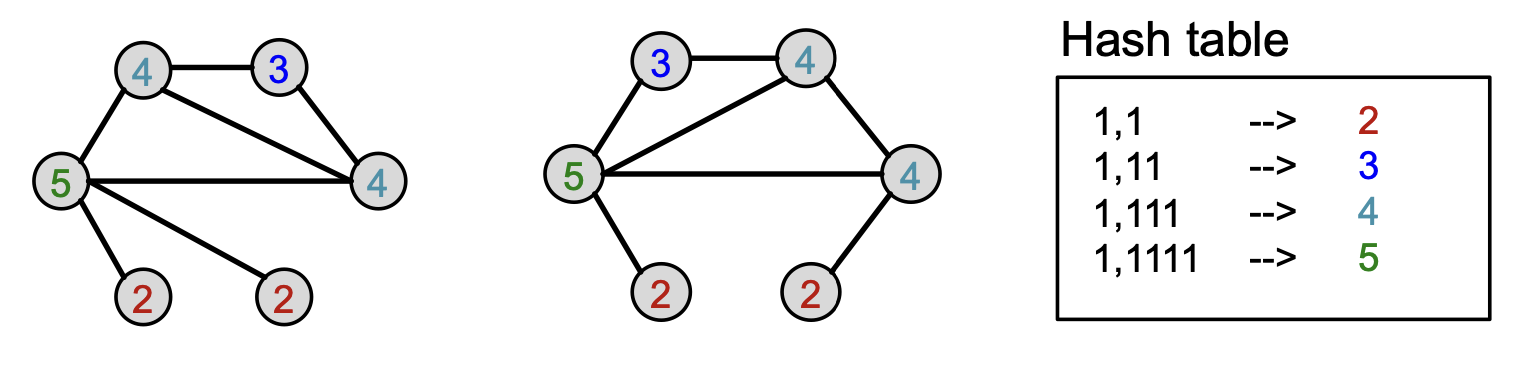
④ 2/3번 과정을 KK번 반복 후 Feature Vector로 표현

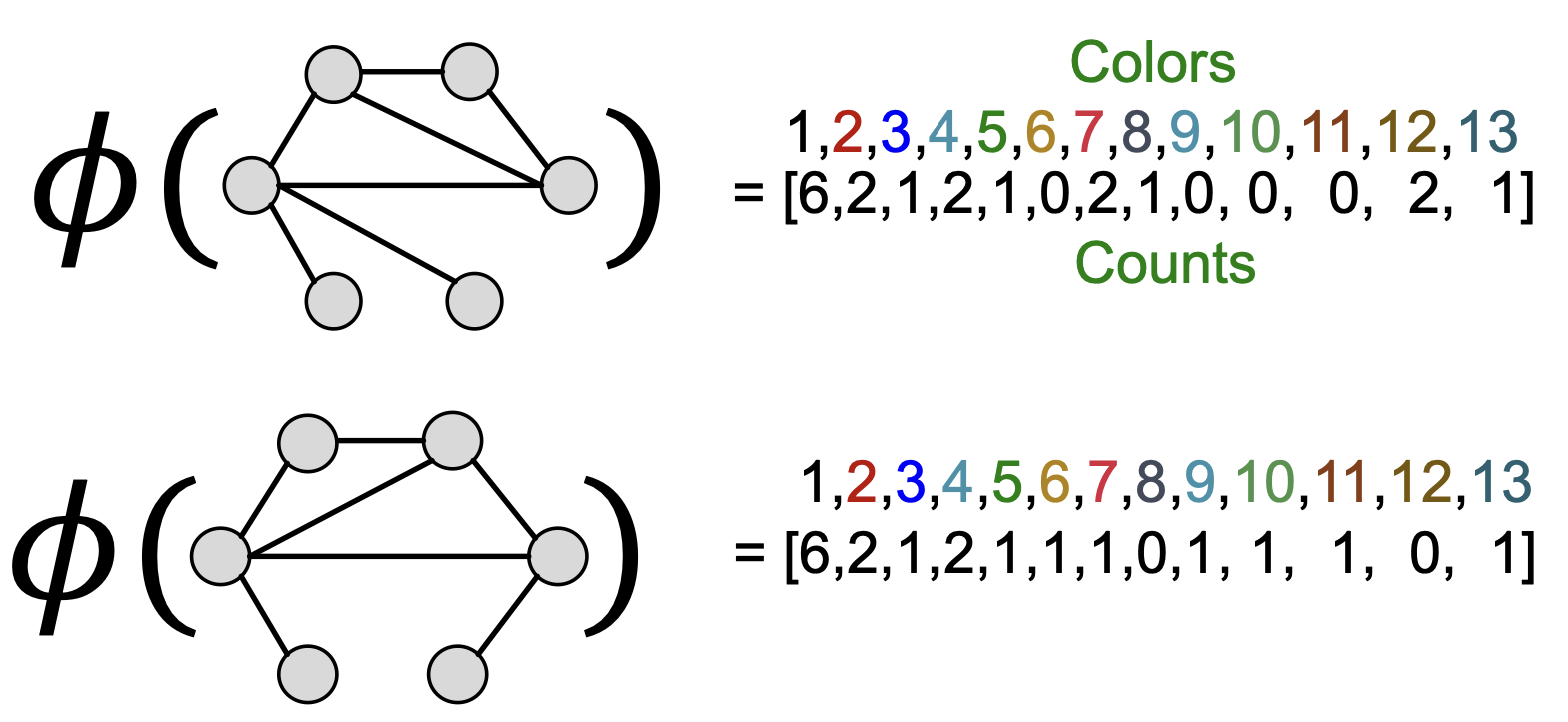
2~3번 과정을 반복하는 부분을 수식화하면 아래와 같이 나타낼 수 있으며,
이때 k = self  ,  u = neighborhoodk\,=\,\text{self}\;,\; u\,=\,\text{neighborhood} 이다.

c(k+1)(v)=HASH({ c(k)(v), { c(k)(u) }u∈N(v)})c^{(k+1)}(v) = \mathrm{HASH}\bigl(\bigl\{\,c^{(k)}(v),\,\{\,c^{(k)}(u)\,\}_{u \in N(v)}\bigr\}\bigr)

KK번 반복한 뒤, 색상별 Node의 개수를 특징으로 삼는 Bag-of-Colors 형태로 Feature를 표현한다.

WL Kernel의 장점
WL Kernel의 계산 비용은 Graphlet Kernel 대비 훨씬 효율적이다.
2/3번 과정의 시간복잡도는 Edge의 개수에 선형적으로 비례하며, 1/4번 과정은 상수 시간만 소요된다.

즉 전체 과정의 시간복잡도는 Edge의 개수에 선형적으로 비례한다고 볼 수 있으며,
이는 Graphlet의 크기에 지수적으로 비례하는 Graphlet Kernel에 비해 훨씬 효율적이다.

profile
Kyeongmin
개발자가 되고 싶은 공장장이🛠
이전 포스트

CS224W #1 Introduction

다음 포스트

CS224W #3 Node Embeddings

0개의 댓글