CS224W #7 Graph Neural Networks (Design)

Kyeongmin·2025년 5월 10일

인공지능

목록 보기

9/9

이 글은 스탠포드 대학의 CS224W(2020) 강의를 듣고 정리한 글입니다.

이번 글에서는 바로 이전 글에서 설명했던 Graph Neural Networks(GNN)의 구조에 이어서 GNN을 실제로 어떻게 활용하고 확장해 나갈 수 있는지에 대해 소개하고자 한다.

GNN Framework

GNN을 실제로 활용할때 어떤 점들을 고려해야하는지 살펴보면, 아래의 5가지로 정리할 수 있다.

Message : 이웃 Node로부터 대상 Node로 정보 전달할 때 변환(Transformation) 과정
Aggregation : 이웃 Node의 정보를 집계하여 새로운 Embedding을 만들어내는 과정
Layer connectivity : GNN Layer를 연결하는 방법 (Stacking, Skip connections 등)
Graph augmentation : 기존의 Graph Structure나 Node의 Feature를 보완하여 Computation Graph를 생성하는 방안
Learning objective : GNN으로 수행할 Task(Node Classification, Edge Prediction 등)

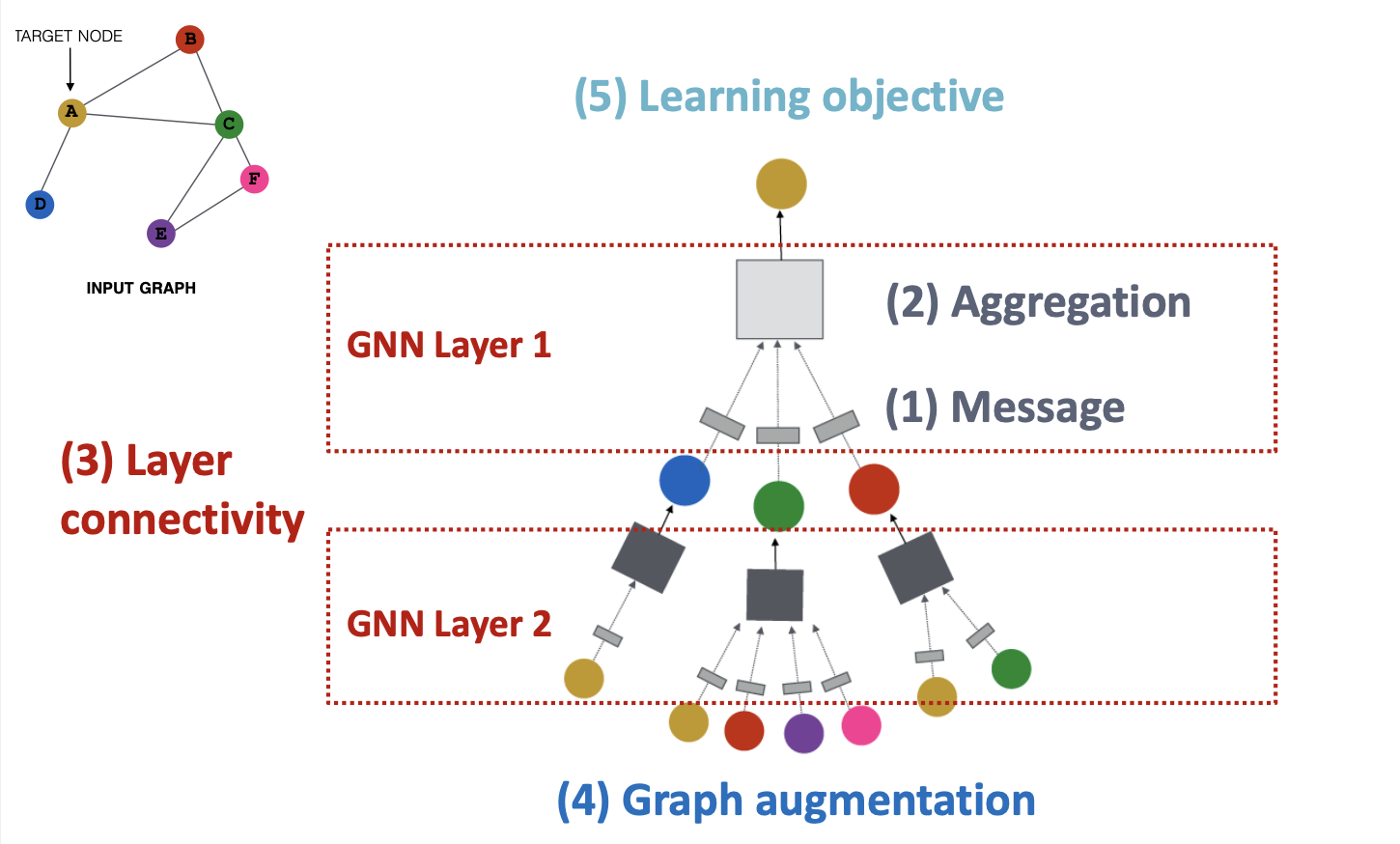
1,2번은 Single GNN Layer 내에서 각각 이뤄지는 연산이며, 3번은 Multi GNN Layer를 다룰 때 고려해야될 부분으로 우리가 GNN 구조를 어떻게 설계하는지와 관련된 부분이고, 4,5번은 GNN Model을 학습시킬때 필요한 과정으로 볼 수 있다.

이번 글에서는 먼저 GNN 구조를 어떻게 설계하는지(1~3번)에 대한 내용을 다루고, 다음 글에서 나머지 부분에 대한 내용을 다룰 예정이다.

Single GNN Layer

하나의 GNN Layer 내부에서는 위에서 언급했던 ①Message Computation, ②Message Aggregation 2개의 단계를 수행하여 특정 Node의 Embedding을 구하게 된다.

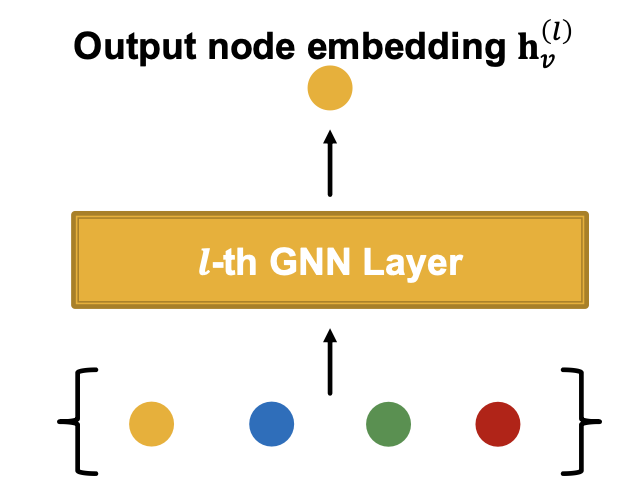
1️⃣ Message Computation

Message Computation은 Node의 현재 상태(Input or Embedding)을 바탕으로 이웃 Node로 전달할 Message를 생성하는 과정이며, 이전 Layer의 Embedding에 선형 변환을 적용하는 것이 하나의 예이다.
(이때 선형 변환을 위한 행렬 $\mathbf{W}$ 는 학습 Parameter이다.)

\mathbf{m}_u^{(l)}=\operatorname{MSG}^{(l)}\left(\mathbf{h}_u^{(l-1)}\right) \quad \cdots \quad \mathbf{W}(l)\mathbf{h}_u^{(l-1)}

2️⃣ Message Aggregation

이웃 Node로부터 전달 받은 Message를 집계하여 새로운 Embedding을 생성하는 과정이다.
이때 집계를 위한 함수는 이전 글에서 언급했듯이, 순서에 불변한(Invariant order) 함수여야한다.
집계 함수의 예시로는 Sum, Mean, Max 등의 연산이 있다.

\mathbf{h}_v^{(l)}=\operatorname{AGG}^{(l)}\left(\left\{\mathbf{m}_u^{(l)}, u \in N(v)\right\}\right) \quad \cdots \quad \operatorname{Sum}\left(\left\{\mathbf{m}_u^{(l)}, u \in N(v)\right\}\right)

Message Aggregation에서는 Node $v$ 의 Embedding을 만드는 과정에서 자기 자신에 대한 정보 손실을 방지하기 위해 이웃 Node의 Message만을 활용하는 것이 아닌 해당 Node의 Message도 함께 활용한다. 즉 아래와 같이 $\mathbf{h}_v^{(l)}$ 를 계산하기 위해 $\mathbf{h}_v^{(l-1)}$ 를 사용한다.

이때 일반적으로, 이웃 Node의 Message를 생성할때 사용하는 행렬과 자기 자신에 대한 Node의 Message를 생성할때 사용하는 행렬은 다르게 설정한다. (아래 Computation의 $\mathbf{W} \leftrightarrow \mathbf{B}$ )
또한 집계 과정에서의 함수는 아래와 같이 CONCAT을 사용하거나 SUM 등의 함수를 사용할 수 있다.

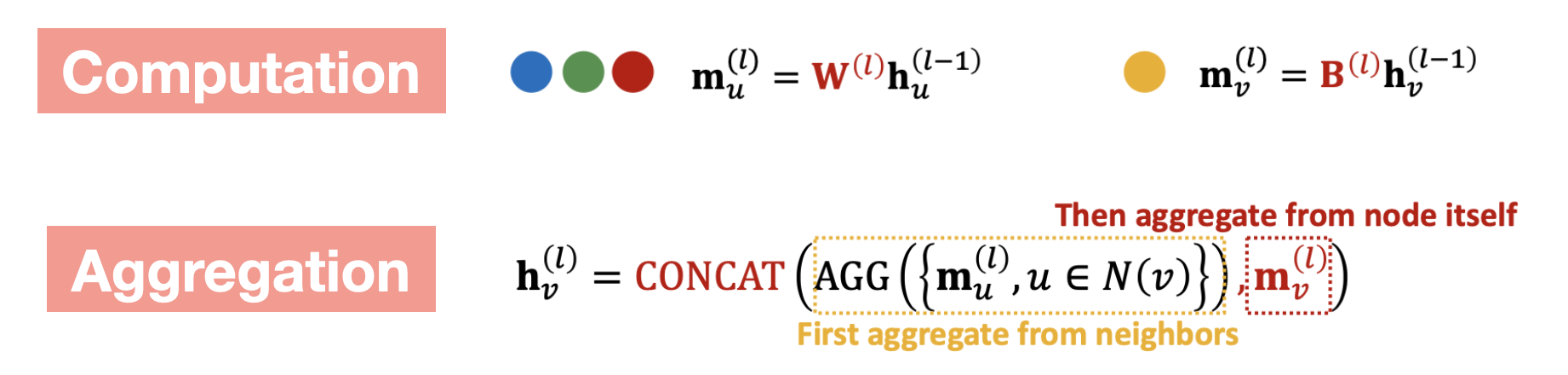
3️⃣ Classical GNN Layer

위에서 언급한 Message Computation/Aggregation 과정을 다양한 관점으로 확장시켜, 다른 Computation 또는 Aggregation 방법을 사용하는 GNN 구조들이 있어 여기에 대해 살펴보고 넘어가자.

GCN

GCN(Graph Convolutional Network)은 아래 수식과 같이 Message Computation에 선형 변환 + 정규화(Normalized), Message Aggregation에 Sum 함수를 적용한 형태이다.
Node Degree(이웃의 수)를 통해 Normalized $\frac{1}{|N(v)|}$ 를 함으로써 Node 간의 차이를 보정한다.

\mathbf{h}_v^{(l)}=\sigma\left( \textcolor{orange}{\sum_{u \in N(v)}} \textcolor{red}{\mathbf{W}^{(l)}\frac{\mathbf{h}_u^{(l-1)}}{|N(v)|}} \right)

GraphSAGE

GraphSAGE는 Embedding 생성을 위해 이웃 Node 뿐만 아니라 자기 자신의 Node 정보까지 활용하는 Embedding에 대한 표현력을 높이는 방법론이다. 아래 수식에서처럼 이웃 Node에 대한 정보 계산(AGG)을 하는 부분과 CONCAT을 통해 자기 자신의 Node 정보를 포함하는 부분으로 구성되어 있다.

\mathbf{h}_v^{(l)}=\sigma\left(\mathbf{W}^{(l)} \cdot \operatorname{CONCAT}\left(\mathbf{h}_v^{(l-1)}, \textcolor{skyblue}{\operatorname{AGG}\left(\left\{\mathbf{h}_u^{(l-1)}, \forall u \in N(v)\right\}\right)} \right)\right)

이때 AGG 함수 내부에 Message Computation/Aggregation 과정이 포함되어 있으며, AGG 함수에는 아래 그림과 같이 Mean/Pool/LSTM 등 다양한 방법을 적용할 수 있다.

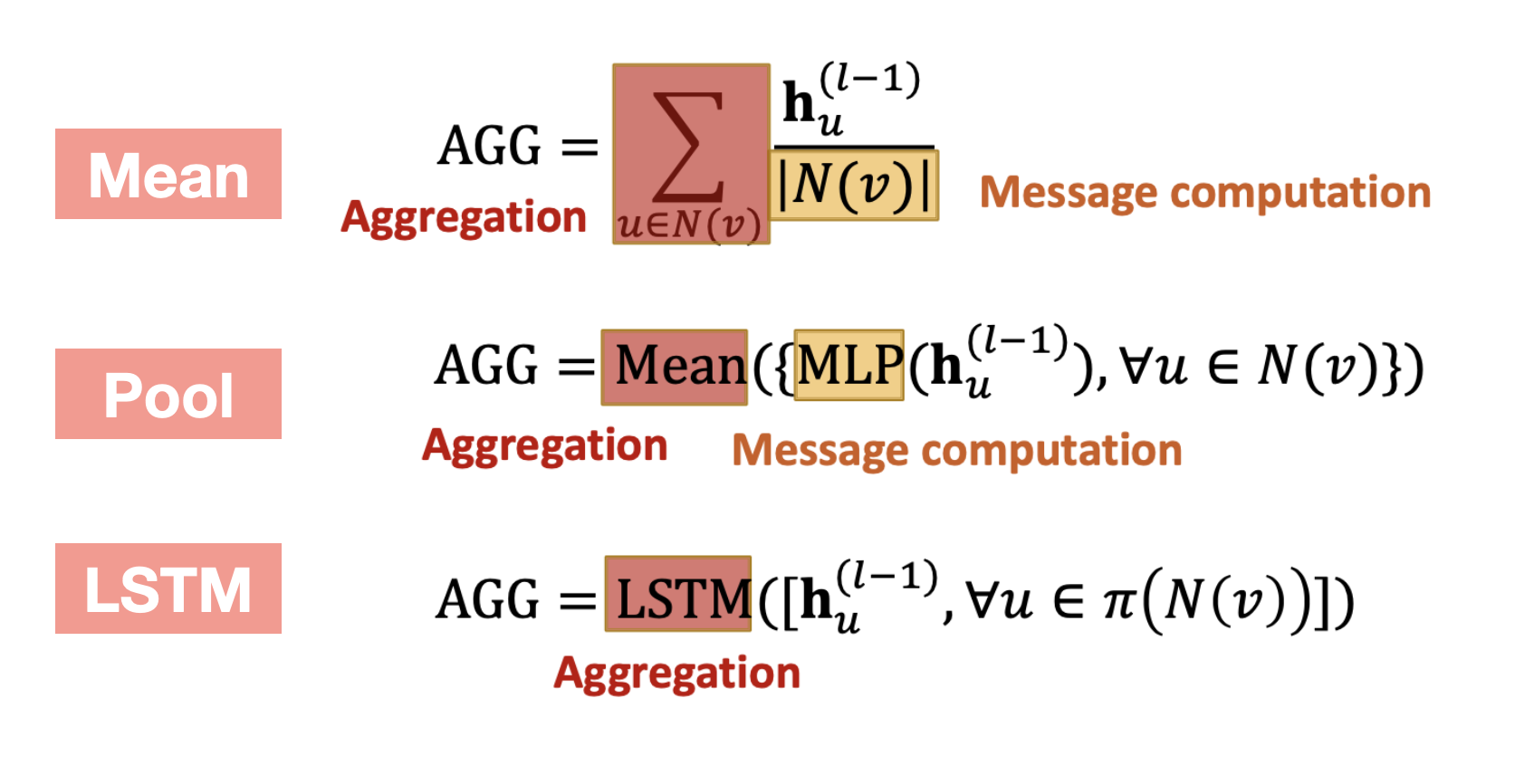
이런 과정을 거쳐 생성된 Node별 Embedding은 서로 다른 Scale을 가지게 되는데, GraphSAGE에서는 이를 보완하기 위해 모든 Layer에서 생성되는 Embedding에 L2 Normalization을 적용하여 Scale을 조정하는 방법을 사용한다.

GAT

GAT(Graph Attention Network)는 GCN 구조에 Attention Mechanism(Attention Weight)을 적용한 방법론으로, 중요한 Node가 가지는 정보를 더 많이 반영하여 Embedding의 표현력을 높이는 방법이다.

\mathbf{h}_v^{(l)}=\sigma\left(\sum_{u \in N(v)} \textcolor{green}{\alpha_{v u}} \mathbf{W}^{(l)} \mathbf{h}_u^{(l-1)}\right)

Attention Mechanism에서 가장 중요한 역할인
Attention Weight는 학습을 통해 구해지는 Parameter로, 다음과 같은 수식을 통해 계산된다.

① 임의의 함수 $a$ 를 통해 Attetion coefficients $e_{vu}$ 를 구한다.
(이때 함수 $a$ 는 Linear Layer, Inner Product 등이 될 수 있다.)

e_{v u}=a\left(\mathbf{W}^{(l)} \mathbf{h}_u^{(l-1)}, \mathbf{W}^{(l)} \mathbf{h}_v^{(l-1)}\right)

② Attetion coefficients의 정규화를 통해 Attetion weight $\alpha_{v u}$ 를 구한다.

\alpha_{v u}=\frac{\exp \left(e_{v u}\right)}{\sum_{k \in N(v)} \exp \left(e_{v k}\right)}

이렇게 구해진 Attention Score $\alpha_{v u}$ 는 여러 층으로 쌓여진 Layer에서 공유하며 사용되는데, 그렇다 보니 Score가 어느 한곳에 수렴하는 것이 쉽지 않다. 이런 문제를 해결하기 위해서 아래 그림과 같이 각기 다른 함수 $a$ 를 통해 구해진 Attention Score와 Embeeding을 집계하여 새로운 Embedding을 만들고 최종적으로 이를 사용하는 Multi-head attention 이라는 개념이 제안되었고 실제로 많이 활용되고 있다.

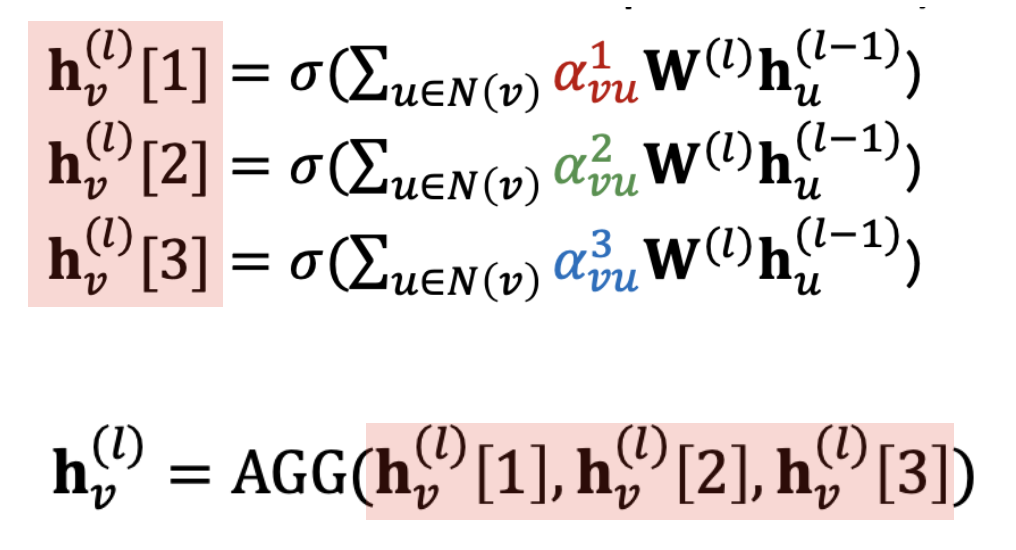
4️⃣ Deep Learning Modules in GNN

Deep Learning 구조를 보다 효율적으로 학습시키기 위해 사용되는 여러 모듈들이 있는데 이를 GNN에도 동일하게 적용시킬 수 있으며, 각각의 모듈들은 Message Computation 과정에 적용된다.

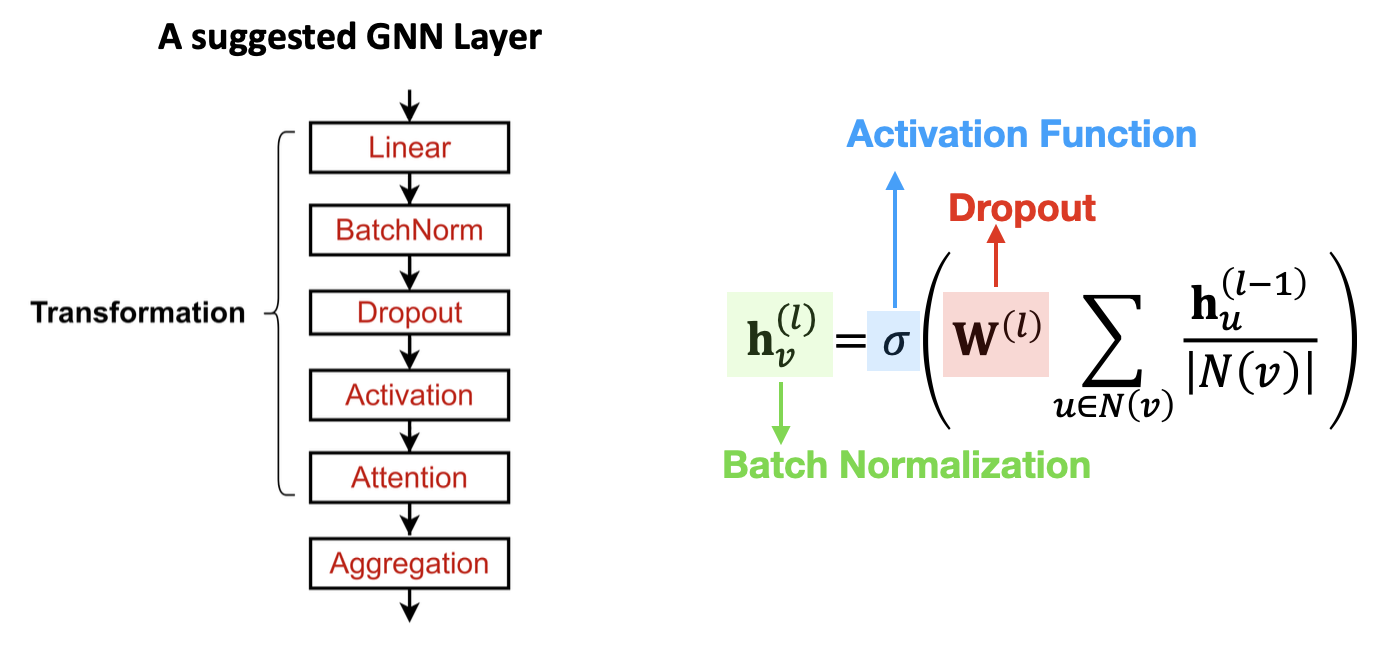
아래 그림에서 Linear Layer는 위에서 소개한 Message Computation $\mathbf{W} (l)\mathbf{h}_u^{(l-1)}$ 과정이고,
그 이후의 학습을 보다 안정적으로 시키기 위한 Batch Normalization, 과적합을 방지하기 위한 Dropout, Non-linearity를 부여하기 위해 사용되는 다양한 Activation Function을 적용할 수 있다.

Multi GNN Layer

GNN Layer를 기존의 Deep Learning에서 Layer를 쌓는 것과 동일하게 연속적으로 Layer를 쌓아 올려서 사용할 수 있다. 그런데 많은 GNN Layer를 거치게 되면, 모든 Node의 Embedding이 유사하거나 같은 값으로 수렴하게 되는 Over-smoothing 이라는 문제가 생기게 된다.

1️⃣ Receptive Field

왜 Over-smoothing이 발생하는지 알기 위해서는 먼저 GNN의 Receptive Field에 대해 알아야 한다.
Receptive Field란, 특정 Node의 Embedding을 구하기 위해 사용되는 Node의 집합을 의미하는데, GNN의 Layer를 쌓게 되면 1개 Node와 관련된 이웃 Node의 범위가 급격하게 증가되고 Receptive Field가 증가하게 된다. (GNN Layer의 수는 이웃 Node의 범위를 의미하는 Hop을 결정한다)

아래 예시에서는 3개 Layer를 쌓았을때, 1개 Node에 대한 Embedding을 생성하기 위해 Graph의 거의 모든 Node를 사용하는 것을 볼 수 있다.

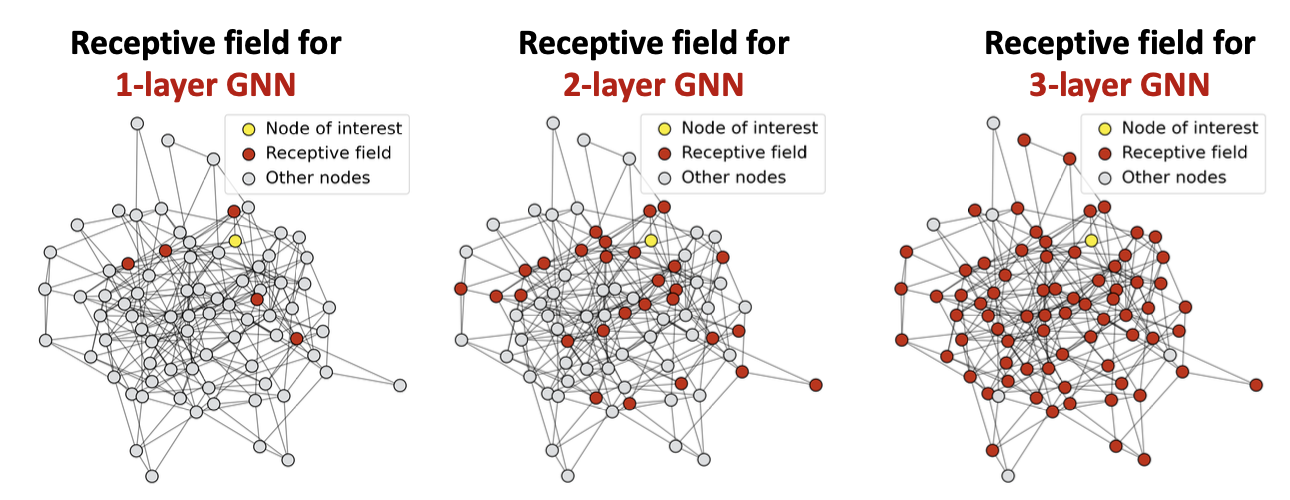
그럼 결국 Layer를 늘리게 되면 다른 Node라도 결국 동일한 정보를 가지고 Embedding을 생성하기 때문에, 유사한 값을 지니거나 같은 값으로 수렴하는 문제가 발생할 수 있다.

2️⃣ Solution

이러한 Over-smoothing 문제를 해결하려면 어떻게 해야할까?

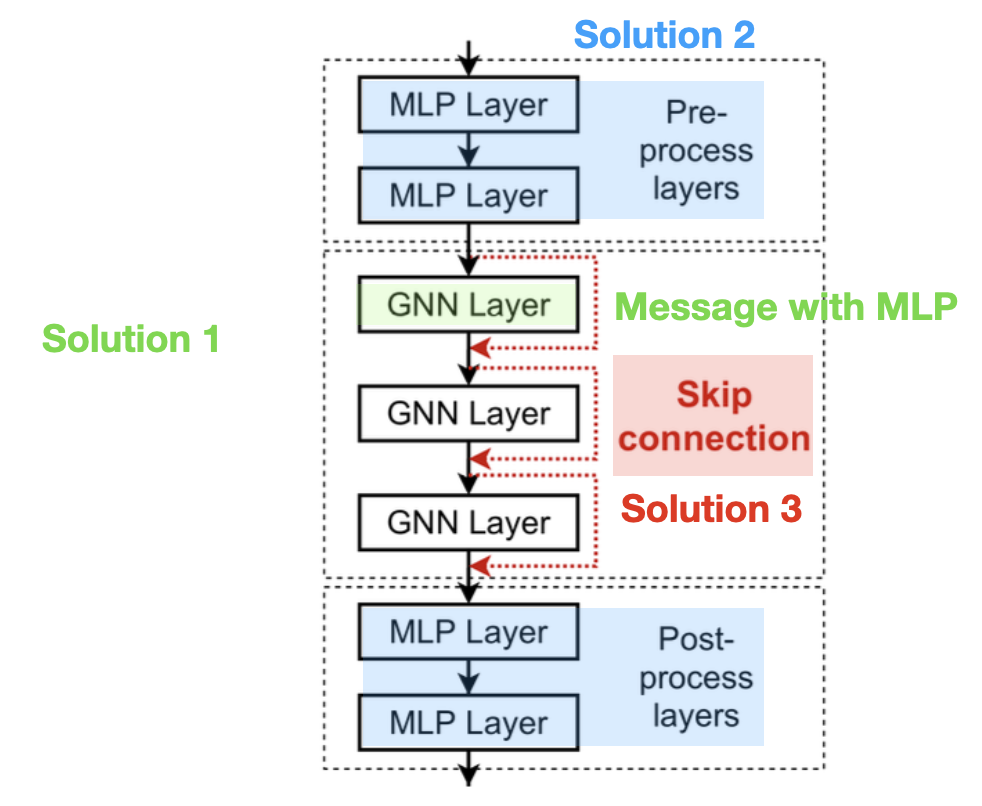
먼저 Graph의 크키를 고려해서 적절한 GNN Layer의 수를 선정하고 개별 GNN Layer의 표현력과 Embedding 성능의 향상에 집중하는 방법(①, ②)이 있으며, 만약 불가피하게 많은 GNN Layer 수를 사용해야한다면 일부 Layer를 Skip하는 방식으로 Over-smoothing 문제를 완화하는 방법(③)이 존재한다.

① Increase the expressive power within each GNN layer
GNN Layer에서 사용하는 Aggregation/Transformation 함수에 MLP를 활용함으로써 기존보다 표현력과 성능을 높일 수 있다.

② Add layers that do not pass messages
Message를 활용하지 않는 MLP Layer를 GNN Layer의 전/후에 추가함으로써 Node Embedding에 성능을 높일 수 있다.

③ Add skip connections in GNNs
이전 Layer의 정보(Embedding)을 직접 활용할 수 있도록 Skip Connection을 추가하여 현재 Layer와 이전 Layer의 정보를 모두 활용할 수 있게 함으로써 Over-smoothing 문제를 완화하고 표현력을 높이는 방법이다.

아래는 위에서 언급한 3가지의 Solution을 모두 활용한 GNN 구조의 예시이다.

Kyeongmin

개발자가 되고 싶은 공장장이🛠

이전 포스트