CS224W #6 Graph Neural Networks (Model)

이 글은 스탠포드 대학의 CS224W(2020) 강의를 듣고 정리한 글입니다.

---

이번 글에서는 Neural Networks를 Graph 구조에 적용한 Graph Neural Networks(GNN, 그래프 신경망)의 기본 개념과 작동 방식을 소개한다.
※ 이전에 작성했던 Graph 구조에서의 Node Embedding에 대한 내용과 연결됩니다.

기존 Shallow Encoding 방식의 Node Embedding은 아래 그림과 같이 Graph의 모든 Node에 대한 Embedding Vector를 담고 있는 Table(Matrix)를 사전에 만들어두고 필요할때 해당 Node에 대한 Embedding Vector를 불러오는 방식이다.

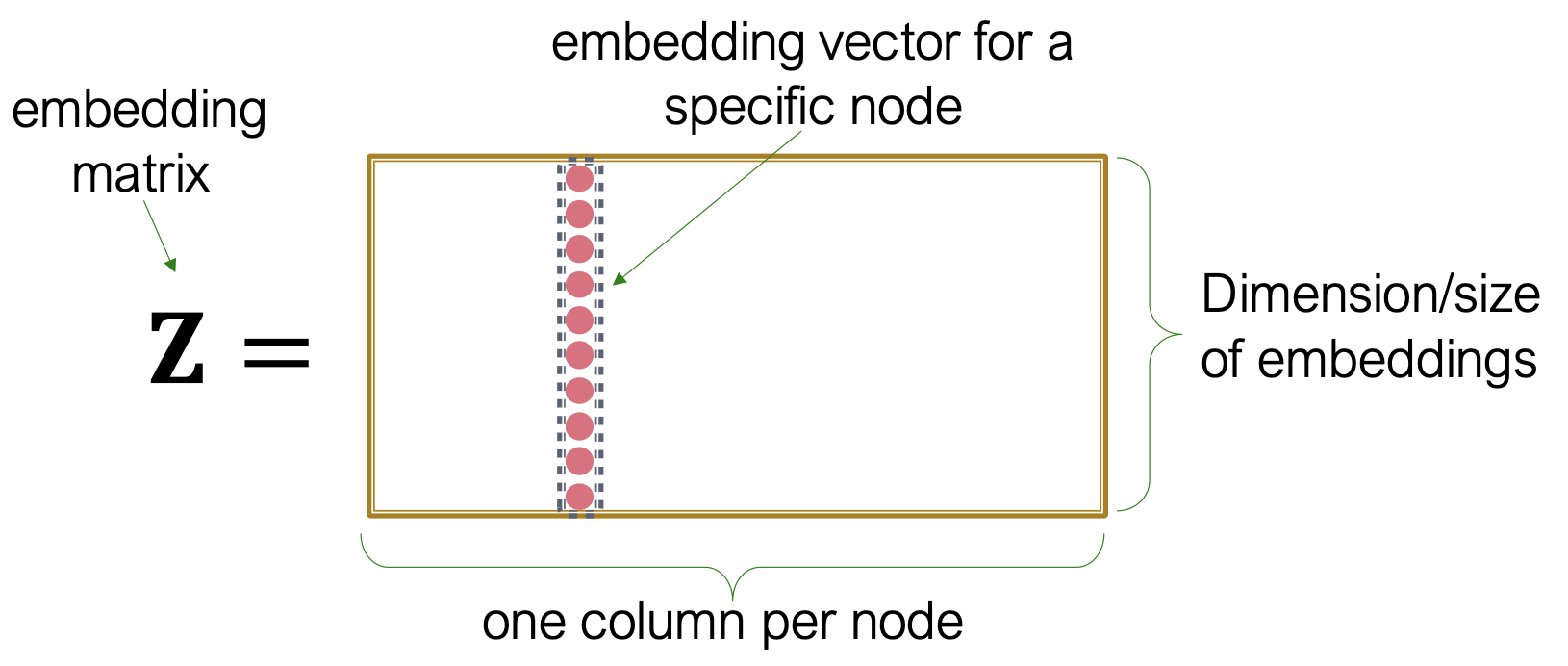
다만 이러한 방식은 ① Node 수가 늘어날수록 증가하는 Parameter 수와 ② 학습되지 않은 Node에 대한 Embedding Vector는 만들어 낼 수 없다는 점, ③ Node의 속성(Feature) 또한 활용하지 못한다는 한계가 존재한다. 이러한 점들을 극복하기 위한 방안으로 Neural Networks를 활용한 Node Embedding이 제안되었으며, 이에 대한 내용을 아래에서 더 자세히 살펴보자.

GNN이란?

앞서 설명한 기존 방식의 한계를 극복하기 위해 제안된 방식으로, 어떤 방식으로 Neural Network를 사용해 Graph 구조를 학습하고 Node Embedding을 할 수 있는지 살펴보자.

Naive Approach

Graph를 Neural Networks에 학습시키기 위해 Graph를 Adjacency Matrix로 나타내어 사용한다고 가정해보자. 그리고 기존 방식에서 Node 속성을 사용하지 못한다는 단점을 개선하기 위해, Adjacency Matrix + Feature에 대한 Vector를 추가하여 Neural Networks로 학습해보자.

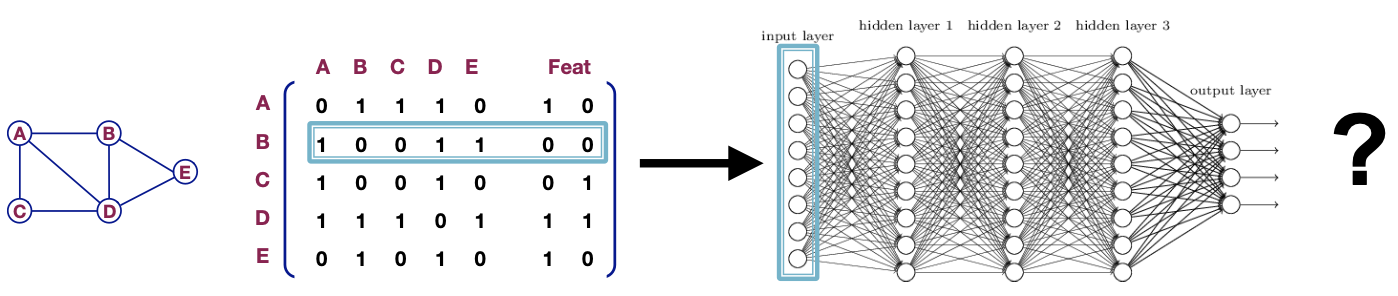
학습은 가능하겠지만, 이러한 방식은 기존 Node Embedding과 동일한 단점들을 가진다.
① Node 수에 비례하여 Parameter를 가진다. $(O|V|\;\text{Parameter})$
② 다른 크기를 갖는 Graph 구조에 적용할 수 없다.
③ Node의 순서에 민감하다. (Sensitive to node ordering)
Graph를 Adjacency Matrix 형태로 나타낼때 A,B,C,D,E ... 와 같이 순서가 정해지는데 만약 이에 대한 순서가 달라지면 결과 또한 달라질 수 있다.

1️⃣ Graph Convolutional Networks

Adjacency Matrix 형태의 데이터를 그대로 사용하면 생기게 되는 문제를 해결하기 위해서, 이미지 분석에 주로 활용되는 Convoultional Neural Networks(이하 CNN)에서 착안하여 Graph에 적합한 구조를 새롭게 구성한 Graph Convolutional Networks(이하 GCN)이 제안되었다.

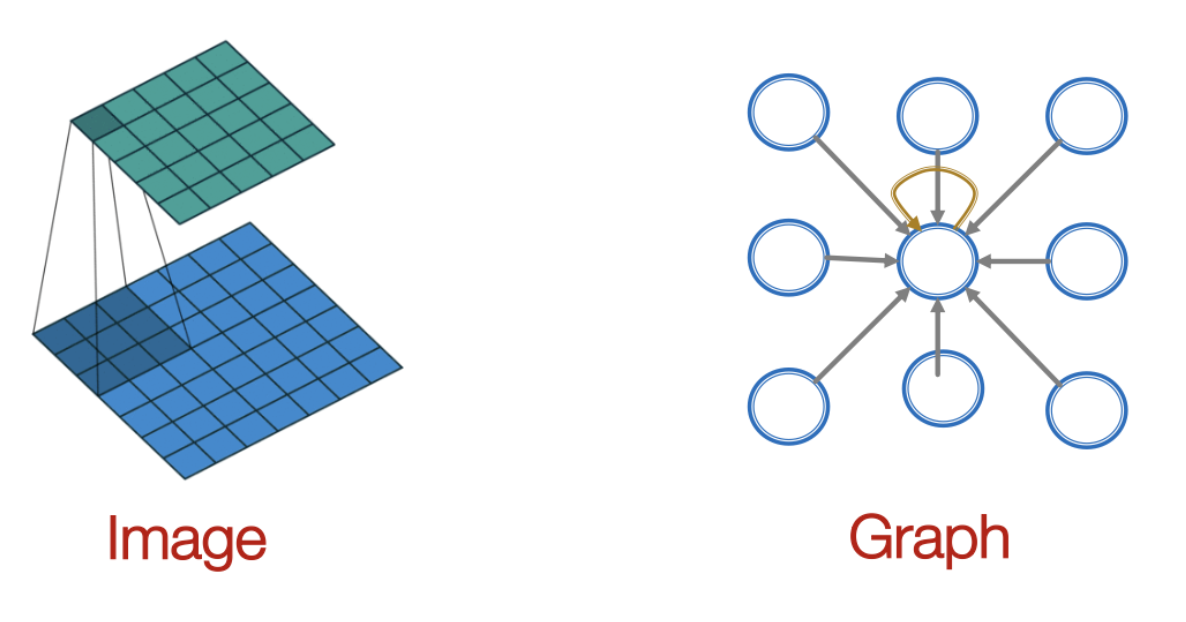
CNN에서 ①이미지를 고정된 크기의 Kernel을 이동해가면서 픽셀로부터 정보를 수집하고, 이를 ②집계하여 새로운 데이터를 생성해나가는 것처럼, GCN에서도 대상 Node의 주변에 연결된 이웃 Node들로부터 정보를 수집하고 집계하여 새로운 정보를 생성(Message Passing)하며, 각 단계에 대한 자세한 내용은 아래에서 확인할 수 있다.

• ① Determine node computation Graph
  이미지에서는 픽셀의 순서(좌측에서 우측)가 정해져있기 때문에 순차적으로 Kernel을 이동할 수 있지만 Graph는 Node 간의 순서를 정의할 수 없기 때문에 모든 이웃 Node의 정보를 수집해오고 이때 이웃 Node의 Hop을 정해둠으로써 계산의 범위를 한정시킨다.
• ② Propagate and transform information
  수집된 정보를 집계 함수를 통해 계산해야하는데, 이때 순서에 상관없이 결과값은 동일해야하기 때문에 순서에 불변한 (Invariant order) 집계 함수를 사용해야한다.

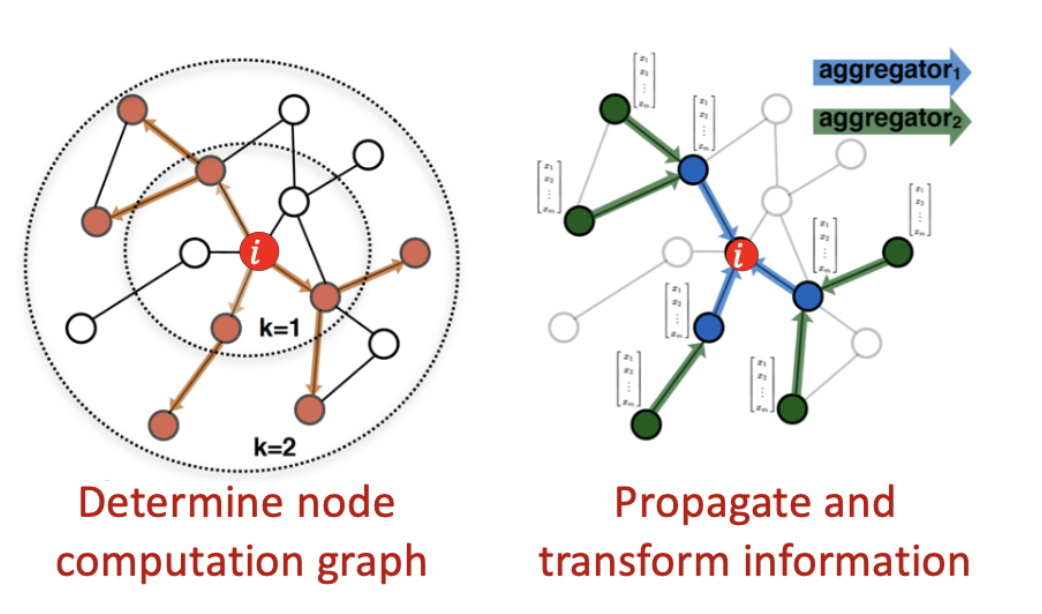
Mechanism

1️⃣ Multi Layer with GCN

Neural Networks에서는 Layer를 여러개 쌓음으로써 모델의 성능을 향상시키는데, GNN에서는 어떤식으로 Layer를 쌓고 어떤 집계 함수가 사용되는지 함께 알아보자.

아래 그림에서 좌측은 입력되는 Graph이고 만약 우리가 이웃의 범위를 의미하는 Hop, $k=2$ 로 설정해뒀다라고 가정하면 우측의 모습처럼 Layer 2개를 가진 GCN 모델이 생성된다.

Layer 0에서는 데이터의 원형(GCN에서 입력 데이터는 일반적으로 Node Feature)이 입력되며, Layer 1/2에서는 각각의 Node에 대한 Embedding Vector가 생성된다. 여기서 Layer는 학습 Parameter로 구성되어 있으며, Node들은 동일한 Layer(Parameter)를 공유하여 사용한다.

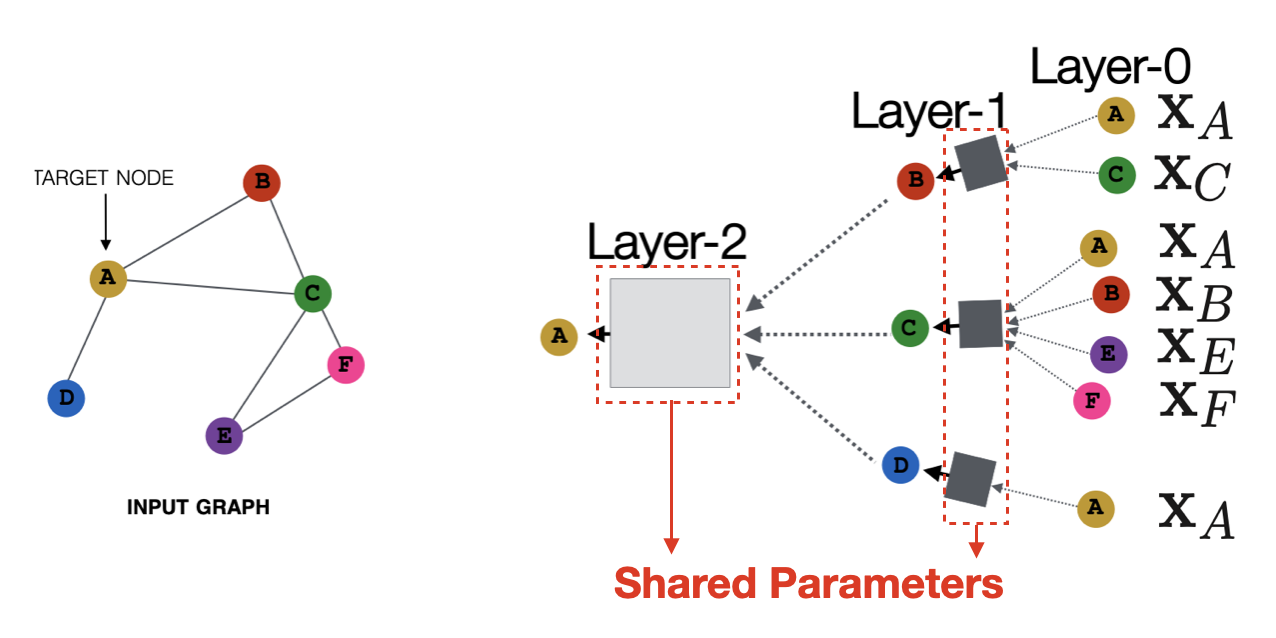
2️⃣ Formulation

각각의 Layer에서 이뤄지는 과정을 수식화하면 아래와 같이 표현할 수 있다.
($h_v^{l}$ : Node $v$의 $l$번째 layer에서 embedding / $W_l, B_l$ : $l$번째 layer의 학습 Parameter)

• 이웃 Node에 대한 집계 함수는 앞서 말했듯이 순서에 불변해야하고, 여기에서는 Sum을 사용했다.
• 각 Layer에서 집계 함수 정보에 현재 Layer에서의 대상 Node의 Embedding 정보를 더하고 있다.
• 최종 Embedding Vector는 $z_v$ 형태로 표현한다.
• $W_l, B_l$는 모두 학습 Parameter로써, Node에 관계 없이 동일한 Layer에서는 공유하여 사용된다.

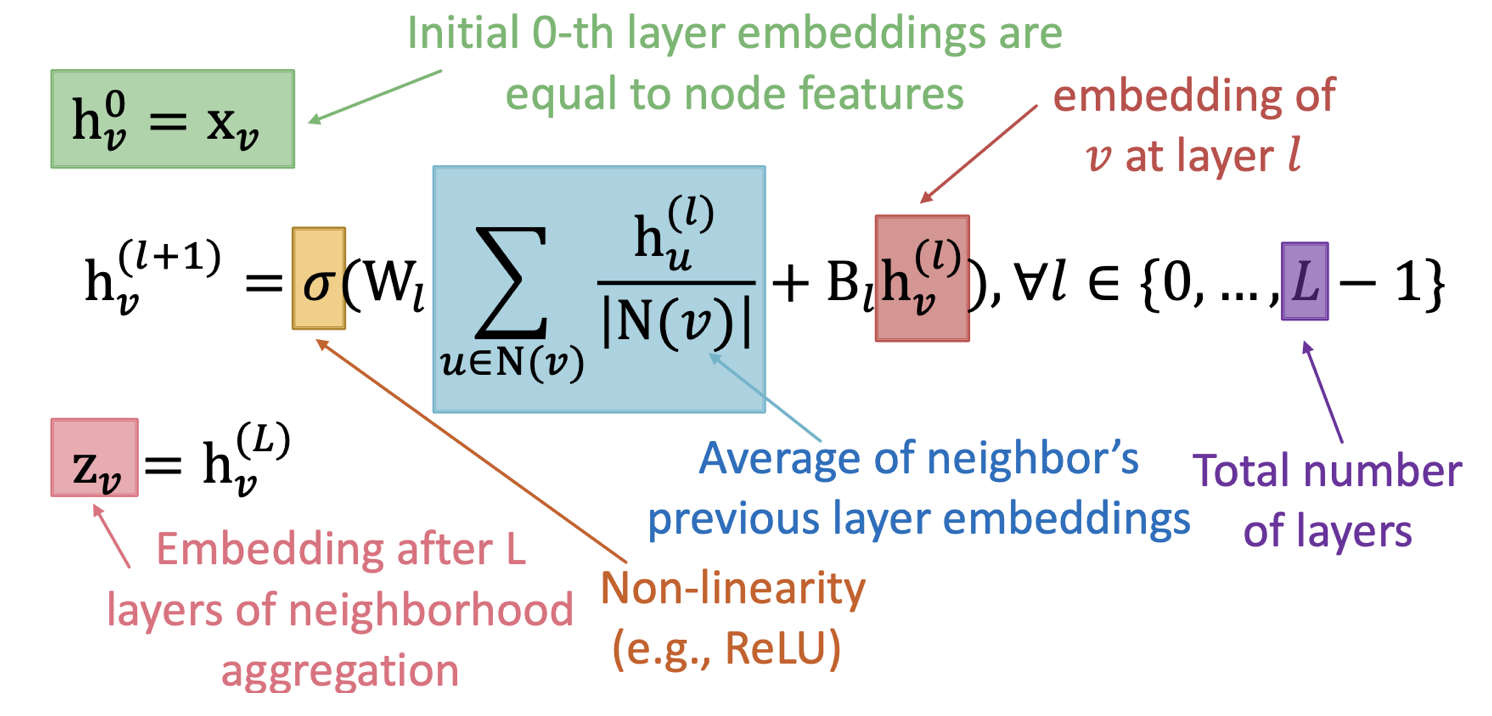
3️⃣ Matrix Formulation

수식을 행렬로 표현하게 되면 이후 학습 과정을 포함한 연산 과정에서 효율성을 높일 수 있기 때문에, 앞서 수식에서 행렬로 표현되지 않은 이웃 Node에 대한 집계 부분을 행렬로 표현해보자.

1. 각각의 Layer에서 Embedding Vector를 행렬 $H$ 형태로 나타낸다.

   $H^{(l)} = \begin{bmatrix} h_1^{(l)} & \cdots & h_{|V|}^{(l)} \end{bmatrix}^{\top}$

2. 이웃 Node에 대한 정보를 더하는 부분은 인접행렬과의 행렬곱으로 나타낼 수 있다.

   $\sum_{u \in \mathrm{~N}(v)} h_u^{(l)} = A_{v,:} H^{(l)}$

3. $|N(v)|$ 를 대각성분으로 가지는 대각 행렬 $D$을 통해 $1\,/\,|N(v)|$을 구할 수 있다.

   $D_{v,v} = \text{Deg}(v) = |\mathrm{~N}(v)\,| \\ D^{-1}_{v,v} = \frac{1}{|\mathrm{~N}(v)\,|}$

4. 위에서 구한 수식을 종합하면 아래와 같다.

   $\sum_{u \in \mathrm{~N}(v)} \frac{h_u^{(l-1)}}{|\mathrm{~N}(v)\,|} \quad \Rightarrow \quad H^{(l+1)} = D^{-1} A H^{(l)}$

이웃 Node에 대한 집계 부분을 행렬로 표현하고 전체 수식을 다시 표기하면 아래와 같다.
아래 수식은 Neighborhood Aggregation과 Self transformation으로 나눌 수 있다.

4️⃣ 장점

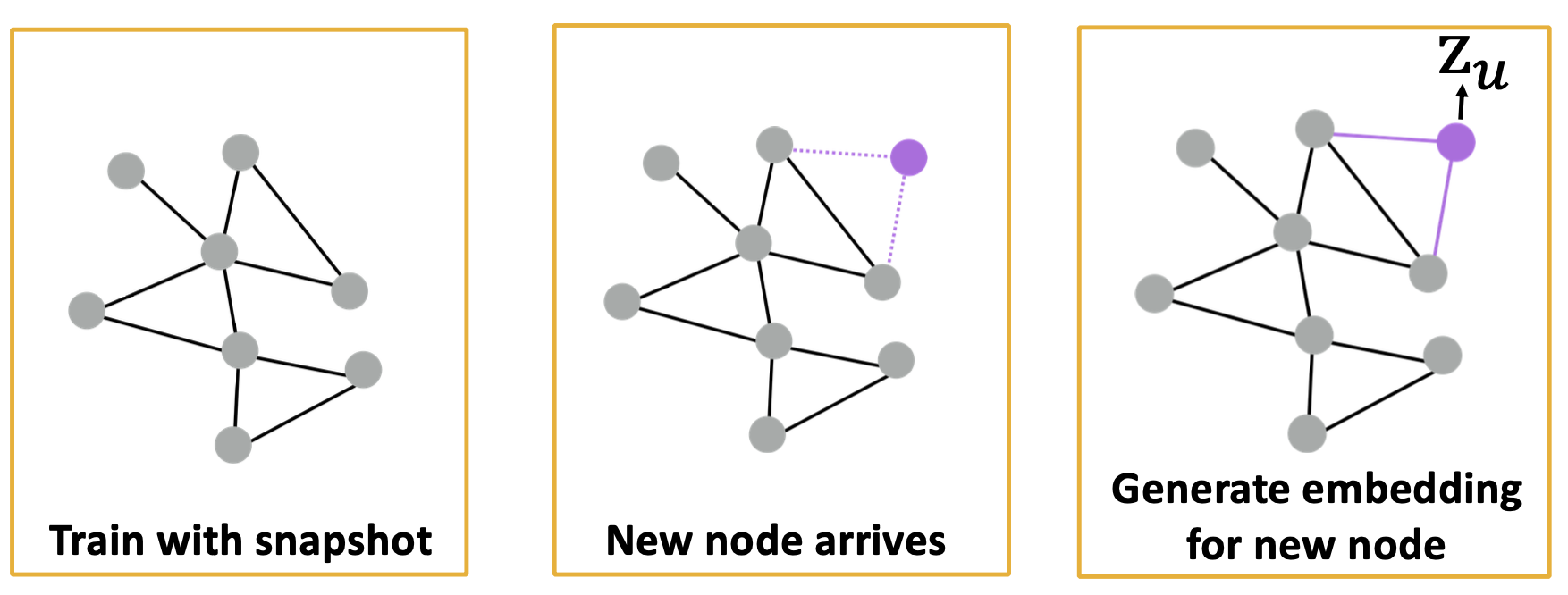
이렇게 학습된 모델은 ① 학습되지 않은 Node와 Graph에 대해서도 Embedding Vector를 생성할 수 있으며(Inductive Capability), ② Parameter의 수가 Node의 수에 비례하지 않기 때문에 효율적인 학습이 가능하다는 장점이 있다.