이 글은 서홍석 교수님의 기초인공지능 강의를 듣고 정리한 내용입니다.
개요
탐색(Search) 문제에는 문제를 해결하기 위한 방법들과 이를 수행하는 에이전트(Agent)로 구성할 수 있다. 에이전트의 유형과 해결 방법에는 어떤 것들이 있는지 살펴보도록 하자.
Agents(에이전트)
에이전트는 주어진 환경에서 어떠한 정보를 가지고 행동하도록 만들어진 것이라고 볼 수 있다.
에이전트는 반응형(Relfex), 계획형(Planning) 구분할 수 있다.
- Reflex Agents(반응형 에이전트) : 현재 상황만을 고려하여 선택한다. (결과는 고려하지 않는다)
- Planning Agents(계획형 에이전트) : 행동에 따른 결과를 고려하여 선택한다.
- Optimal(최적 해) / Complete(단순 해)
- Planning(모든 경우의 수 고려 후 행동) / Replanning(제한된 경우의 수 고려 후 행동)
Search problems(탐색 문제)
에이전트가 문제에 대해 어떤 선택을 해야하는지 판단하는 것을 여기서 탐색 문제라고 한다.
1. 탐색 문제의 구성요소
1) A state space(상태 공간) : 모든 상황 또는 경우의 수
- World state : 주어진 환경에 대한 모든 상태 정보를 말한다.
- Search state : 주어진 문제에 따라 필요한 상태 정보를 말한다. (Search state ⊂ World state)
2) A successor function(후계 함수) : 행동에 대한 결과를 나타내는 함수
3) A start state and a goal test(초기 상태와 목표 도달 여부에 대한 판단 함수)
탐색 문제에 대한 solution은 초기 상태로부터 목표 상태까지의 연속된 행동으로 이루어져 있다.
2. State space 예시
아래의 팩맨 게임에서의 World state, Search state를 확인해보자.
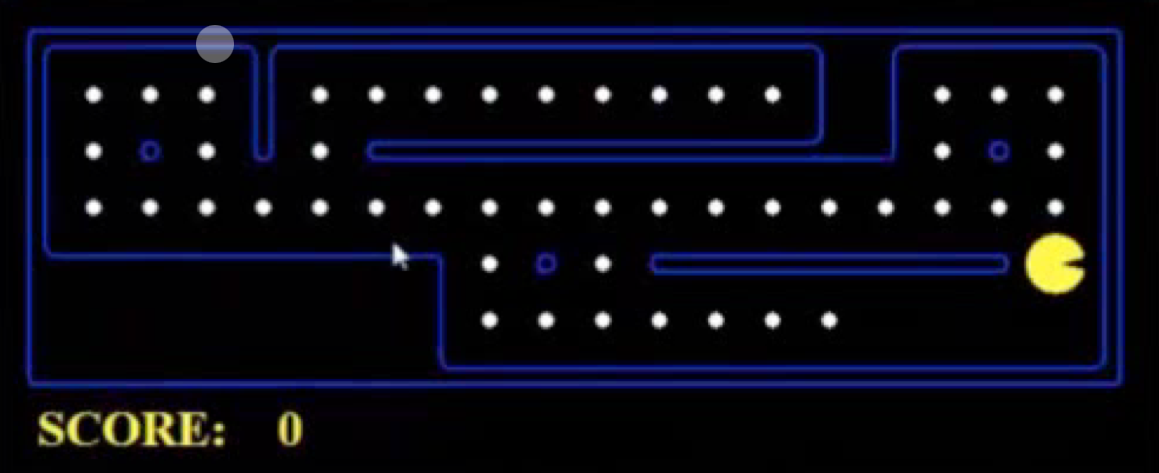
- World state : 팩맨 게임의 모든 정보를 포함한다. (점/팩맨의 위치, 남은 점의 개수, 점수 등 ..)
- Search state : 문제에 따라 Search state를 포함한 Search problem의 구성요소가 달라진다.
- Pathing Problem
- States : (x,y) location
- Actions : NSEW
- Successor : update location
- Goal test : is (x,y) = END
- Eat-All-Dots Problem
- States : (x, y) location, dot booleans
- Actions : NSEW
- Successor : update location and possibly a dot boolean
- Goal test : dots all false
- Pathing Problem
아래의 팩맨 게임에서의 State space의 크기를 확인해보자.

- World state
- Agent positions(120), Food count(30), Ghost positions(12), Agent facing(NSEW)
- State size
- World state =
- State(Pathing) =
- State(Eat-all-dots) =
3. State space graph(상태 공간 그래프)
- 문제를 정의하기 위해 사용되는 구조이다.
- State space에 대해 그래프의 형태로 표현하여 각 state들의 관계를 나타낸다.
(Node → State, Arcs → Sussessors) - 각각의 state는 1번만 나타난다.
- 대부분의 문제에서는 메모리의 한계로 그래프 전체를 그릴 수 없다.
4. Search tree(탐색 트리)
- 문제를 해결하기 위해 사용되는 구조이다.
- 행동 이전 State와 행동 이후 State를 Tree 형태로 표현한다.
(Root Node → Start state, Child Node → Successor) - 각각의 state는 여러번 나타 날 순 있는데, 그래프와 달리 순서에도 의미가 부여되기 때문이다.
- Cycle 발생 가능성이 있어 거의 대부분의 문제에서 트리 전체를 그릴 수 없다.
Search Algorithm(탐색 알고리즘)
※ 탐색 알고리즘의 중요 요소
- Fringe : 트리에서 다음 노드로써의 선택(관심) 대상
- Expansion : 트리 가지의 확장
- Exploration strategy : 트리 탐색에 대한 전략
※ Exploration strategy의 성능 요소
- Complete (해가 존재할때, 해를 반드시 찾아내는가?)
- Optimal (최적해를 찾아내는가?)
- Time complexity (시간이 얼마나 소요되는가?)
- Space complexity (공간을 얼마나 사용하는가?)
※ 탐색 알고리즘의 주요 변수
- b : branching factor(분기 요소), 분기가 가장 많을때의 수를 의미함
- d : depth of the least-cost solution(최적해의 깊이)
- m : maximum depth(최대 깊이)
아래에서 소개할 알고리즘들은, 목표에 대한 정보를 사용하지 않는 즉 Uninformed Search Strategies에 대한 것들이다. 정보를 사용하는 Informed Search Strategies는 다음 장에서 다룰 예정이다.
1. Depth-First Search(DFS; 깊이 우선 탐색)
높은 Depth를 먼저, 즉 Deepest Node를 먼저 Expand 하는 방식이다.
마지막에 들어온 Node를 먼저 선택하는 LIFO(stack) 구조를 사용한다.
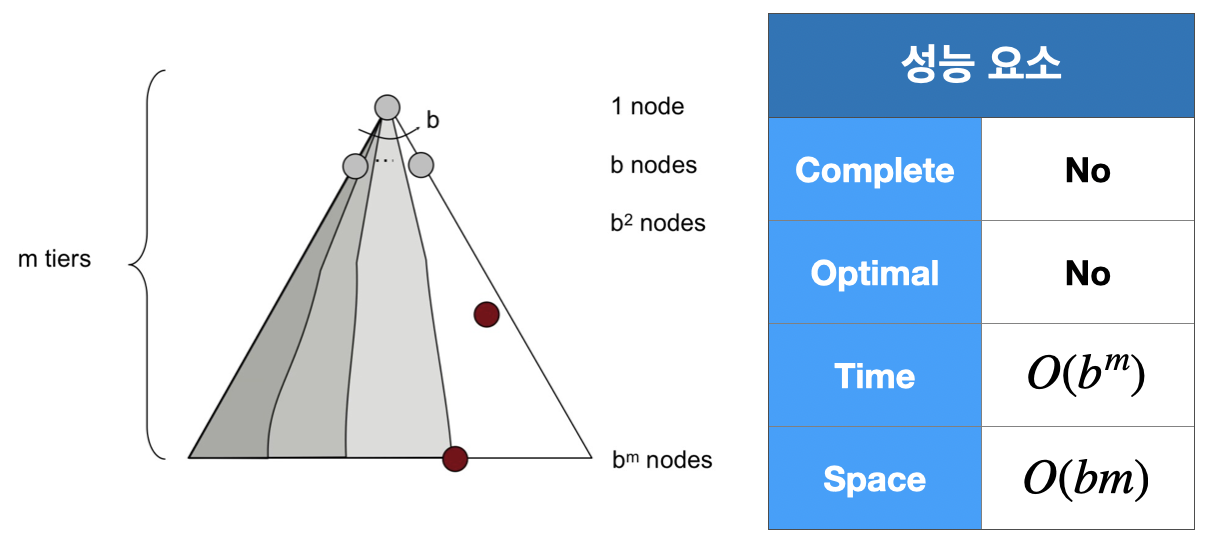
만약 Cycle이 없거나 회피할 수 있다면 DFS를 이용하여 해를 찾아낼 수 있다.
2. Breadth-First Search(BFS; 너비 우선 탐색)
낮은 Depth를 먼저, 즉 Shallowest Node를 먼저 Expand 하는 방식이다.
마지막에 들어온 Node를 먼저 선택하는 FIFO(queue) 구조를 사용한다.
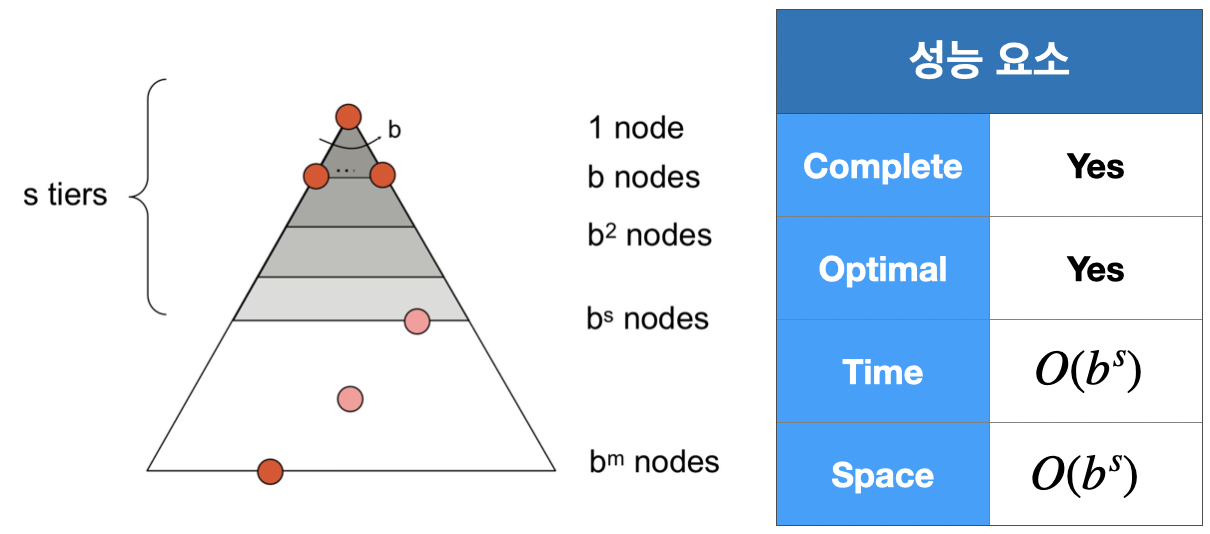
BFS는 최적해를 구할 수 있지만, 모든 cost가 동일한 경우에만 최적해를 구할 수 있다.
cost가 다른 경우에는 최적해를 구할 수 없다.
3. Itrative Deepening
DFS의 장점인 공간 복잡도와 BFS의 장점인 시간 복잡도 2마리 토끼를 모두 잡고자 하는 전략이다.
DFS를 실행하되, 깊이에 대한 Limit을 0부터 1씩 늘려가면서 해를 찾을때까지 반복하는 방법이다.
중복 탐색을 하게 된다는 단점은 있지만, 최적해가 얕은 깊이에 있을수록 성능이 좋다.
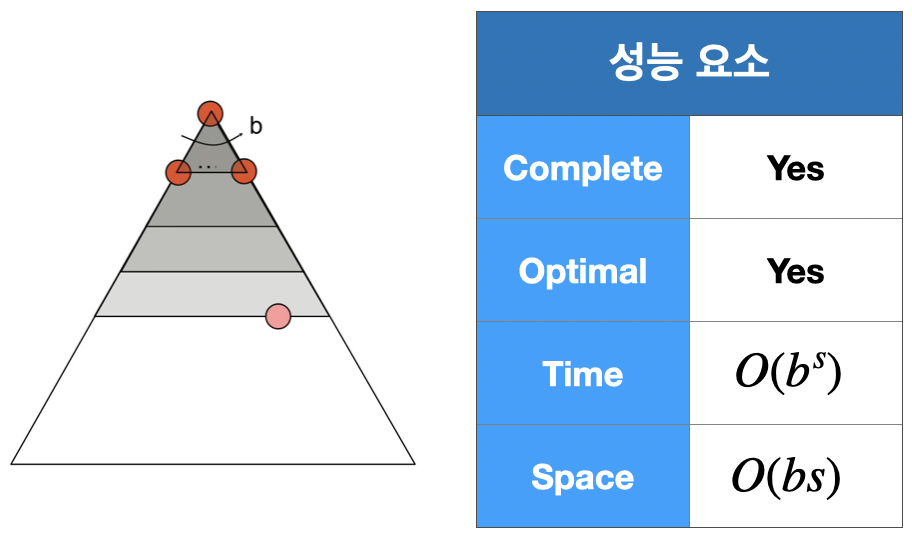
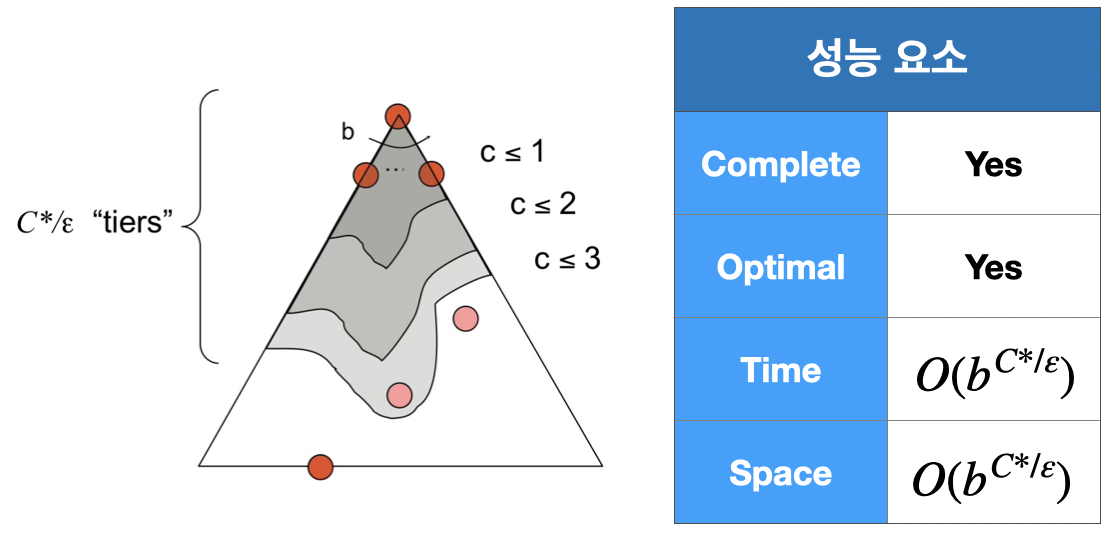
4. Uniform-Cost Search(UCS; 균일 비용 탐색)
Cost가 가장 저렴한 Node를 먼저 Expand 하는 방식으로 Cost가 다른 경우에도 최적해를 찾을 수 있다.
Fringe를 위해 Priority queue(우선순위 큐)를 사용한다.