기계학습 #1 Linear Regression

이 글은 김승룡 교수님의 AAI107 기계학습 강의를 듣고 정리한 글입니다.

---

개요

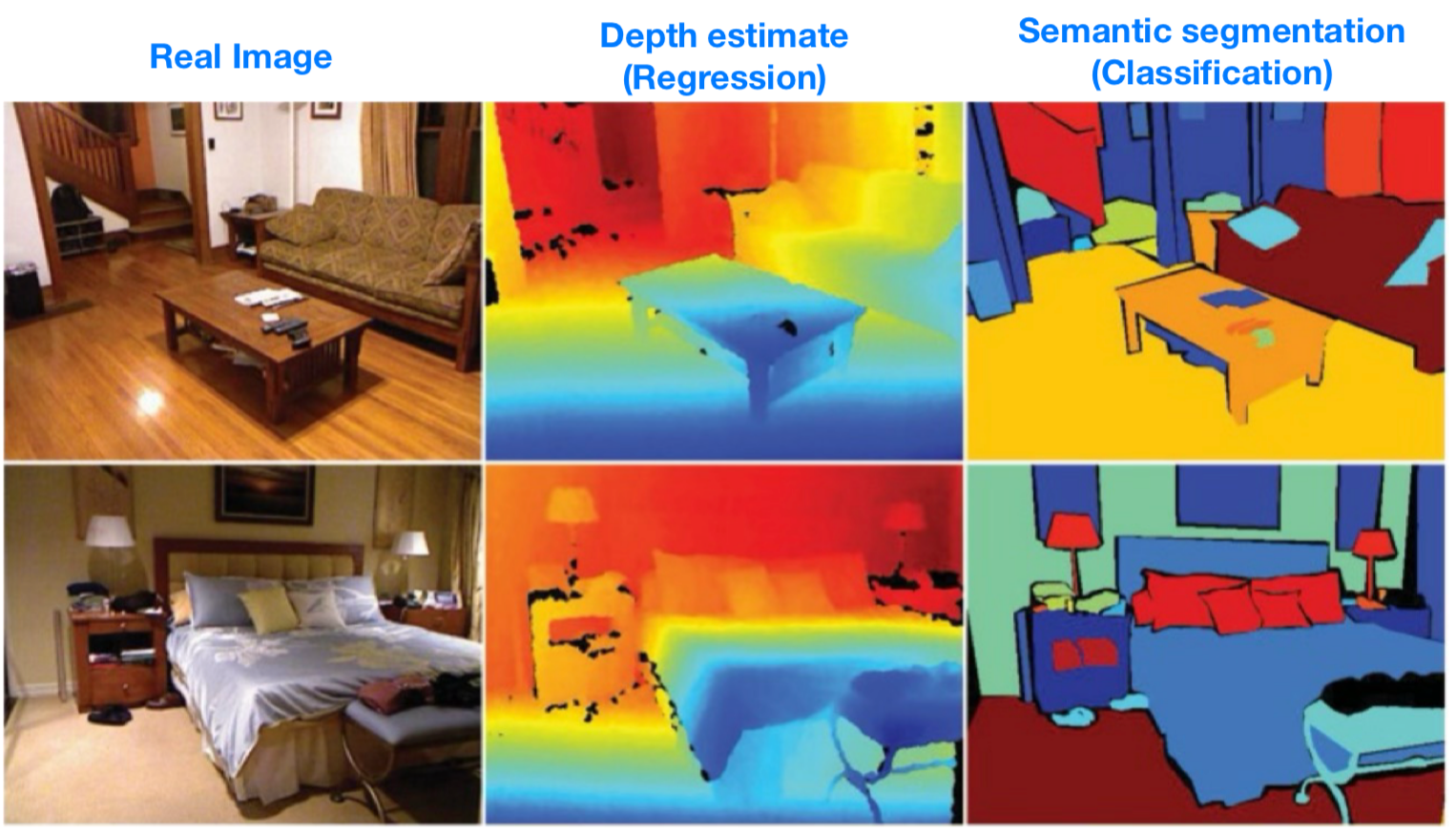
컴퓨터 비젼 분야에는 Depth estimate(깊이 추정), Semantic segmentation(의미적 분할) 2가지 개념이 있다.
Depth estimate은 3차원 공간의 각 픽셀에서 깊이라는 연속값으로 추정하는 방식이다.
Semantic segmentation은 3차원 공간의 각 픽셀을 객체라는 이산값으로 추정하는 방식이다.
여기서 연속값을 추정하는 건 Regression(회귀), 이산값을 추정하는 건 Classification(분류) 라고 할 수 있다.

Regression(회귀)

위에서 컴퓨터 비젼 분야의 Depth estimate를 예로 들어 연속값을 추정하는 것이 Regression 이라고 말했다.
그렇다면 컴퓨터 비젼(이미지)이 아닌 정형 데이터에서의 Regression을 확인해보자.

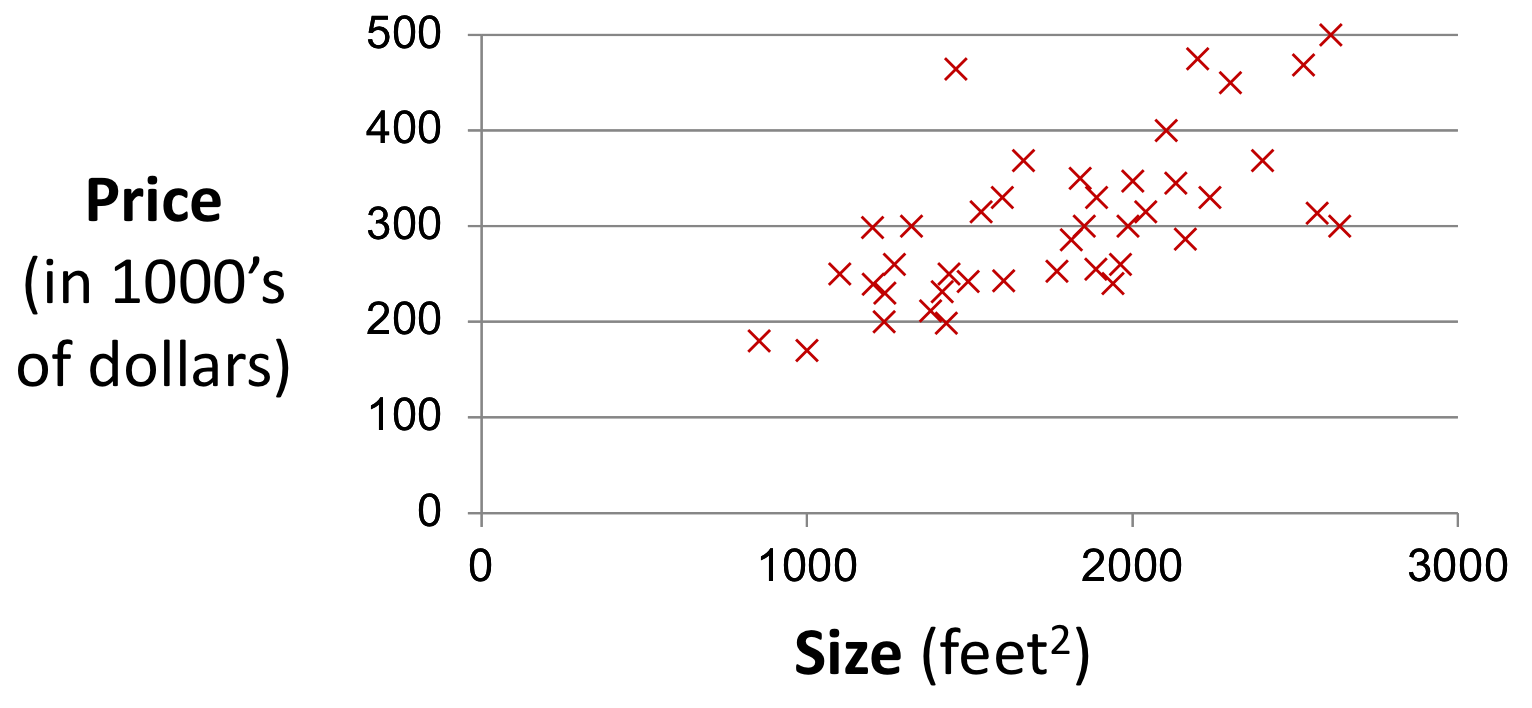
위의 데이터에서 Regression을 적용해보자.
우리는 변수 사이의 관계를 가지고, Size 변수로부터 Price 변수를 추정할 수 있다.

이를 통해 Regression에 대해 정의하자면 아래와 같이 말할 수 있다.

1. 정의

• input 변수로부터 output 변수를 추정하는 것
• input 변수가 output 변수에 미치는 영향을 이해하는 것

2. 데이터

• D차원의 vetcor input 변수 x와 output 변수 y의 쌍으로 구성
• Dataset size : x, y 쌍의 개수
• D : Dimensionality(차원)

또한 Regression의 절차를 보면 아래와 같다.

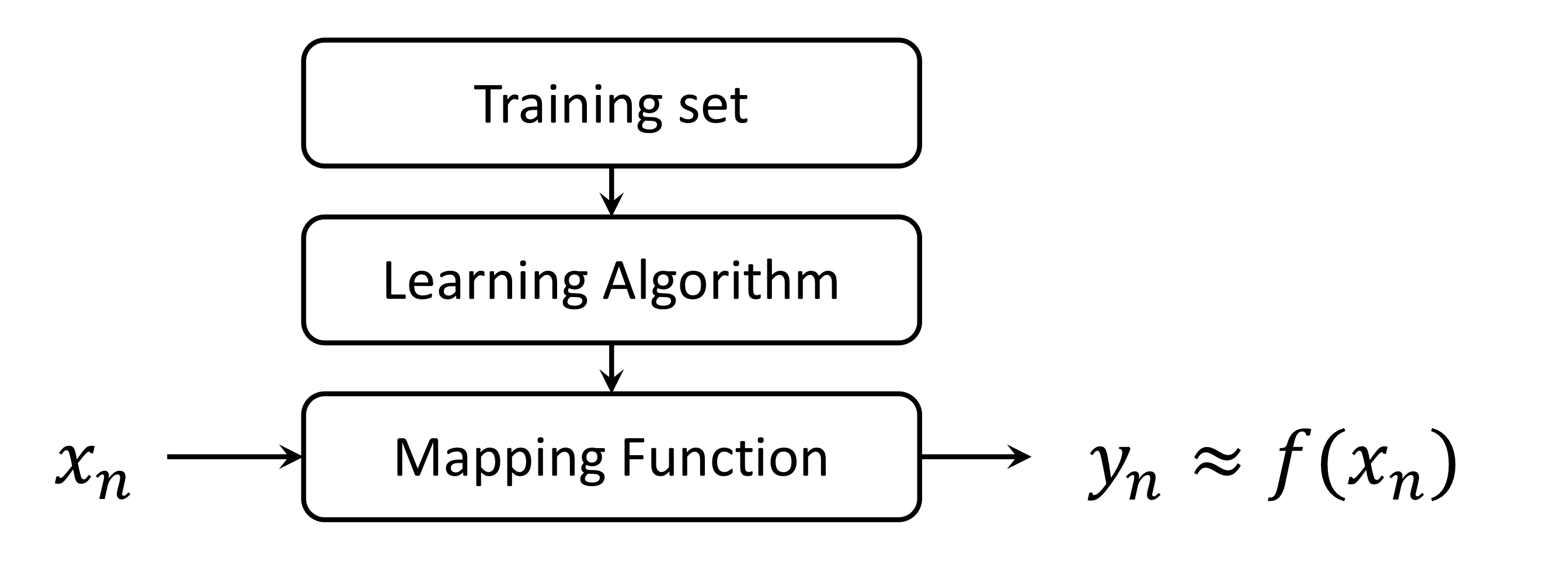
위에서 보다시피, Mapping Function을 통해 x로부터 y를 추정한다.
다만 y를 잘 추정해내기 위해선 주어진 데이터로부터 Learning Algorithm을 통해 Mapping Function을 "충분히 잘" 찾아내어야 한다.

Linear Regression(선형 회귀)

그렇다면 Learnig Algorithm 중 하나인 Linear Regression을 예로 들어보자.

그런데 많고 많은 방법 중에 왜? Linear Regression을 예로 드는걸까?
간단하고, 이해하기 쉽고, 많이 사용될 뿐만 아니라 비선형 모델로도 쉽게 만들 수 있기 때문이다.
가장 중요한 이유는, 이 모델 하나로 머신러닝 대부분의 근본적인 컨셉을 배울 수 있기 때문이다.

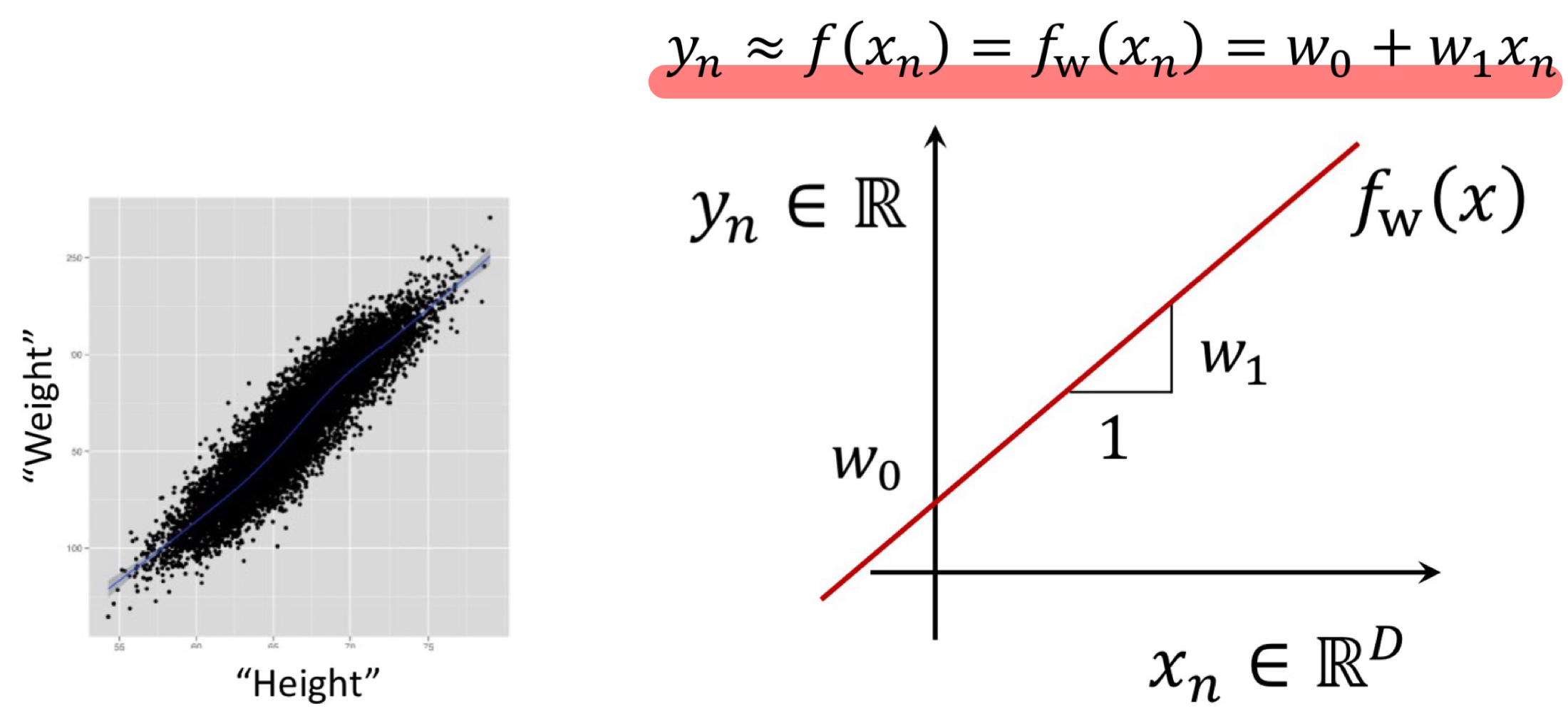
Linear Regression이란, input ↔︎ output 간 선형 관계를 통해 output 변수를 추정하는 방법이다.
따라서 위 그림과 같이 Mapping Function은 선형식과 같은 형태를 가진다.
(위 그림의 예시는 $y = ax+b$ 꼴과 같이 직선의 방정식 형태를 지니고 있음을 알 수 있다.)

1. Learning(학습)

Linear Regression은 Learning Algorithm이고, x에 대한 선형식은 Mapping function이다.

Learning Algorithm의 목적은 Mapping Function을 잘 찾아내는 것이므로,
Linear Regression에서는 x에 대한 선형식, 즉 최적의 $w^*$를 찾아내는 것이라고 할 수 있다.

우리는 이 과정을 Learning 이라고 말한다. (or estimating, fitting)
Learnig을 위해서는 다음에 나오는 Cost Function과 Optimization Algorithm에 대해서 알아야 한다.

2. Cost Function(비용 함수)

1) 정의

먼저, 우리는 최적의 $w^*$를 어떻게 추정할 수 있을까?
아래의 그림처럼 임의의 데이터와 함수($f_w(x_n) = w_0 + w_1x_n$)를 설정하고 $w$에 임의의 값을 대입해보자.

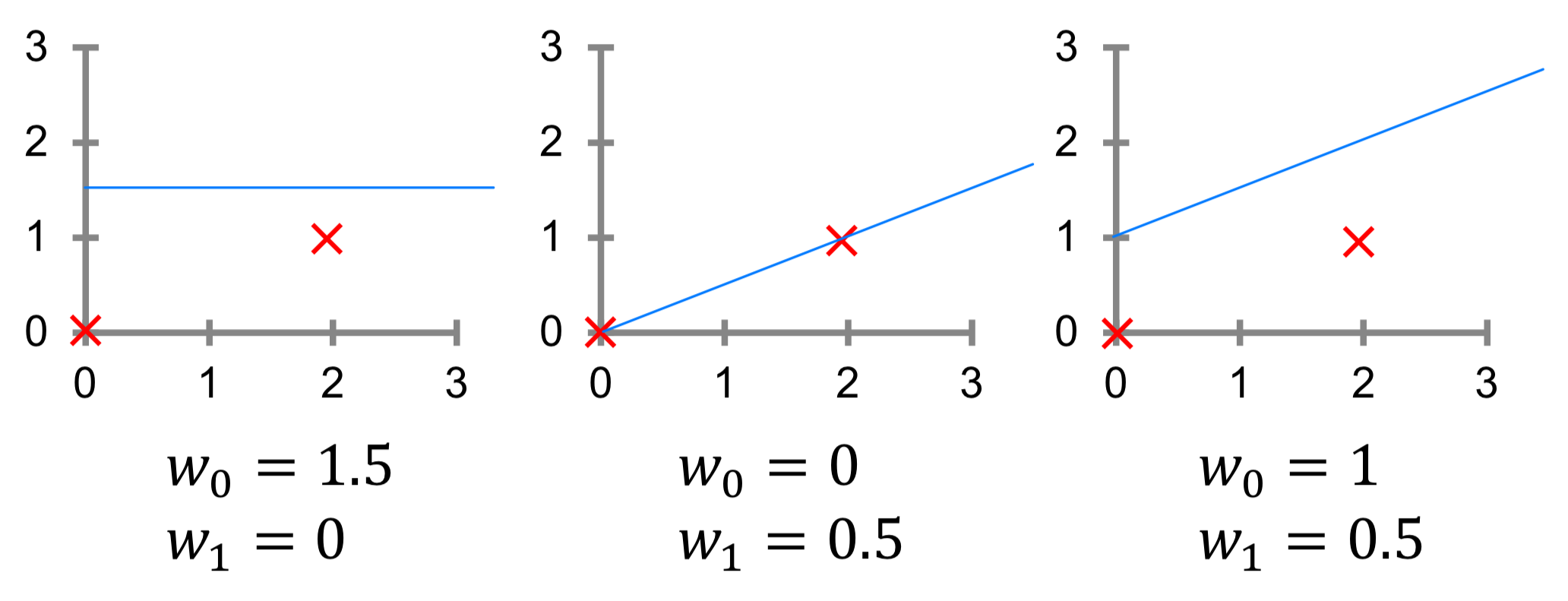
3가지 경우 중 어떤 $w$의 값이 최적이라고 말할 수 있을까?
$f_w(x_n)$과 $y_n$ 사이의 오차가 적은, 다시 말해 $x_n$에 대해서 $y_n$을 잘 추정하고 있는
$w_0=0, w_1=0.5$ 라고 말할 수 있다.

이를 통해서 최적의 $w$는 주어진 데이터 $\{ (x_n,y_n)^N_{n=1} \}$ 로부터 $f_w(x_n)$이 $y_n$에 가장 가까워지게 하는 $w$라고 볼 수 있다.

1️⃣ 최적의 $w$를 구하는 과정을 수식으로 나타내면 아래와 같다.

• 오차를 제곱 하는 이유
  : 양수 오차와 음수 오차를 더했을때 오차가 없음을 뜻하는 0이 되는 것을 방지하기 위함이다.

  2제곱이 아니라 3제곱, 4제곱 등도 가능하며, 단순 절댓값을 씌워도 상관없다.
  2제곱을 쓰는 이유는 최적화 부분에서 다시 설명하겠다.

• $\frac{1}{N}$ 이유
  : 각각의 데이터가 가진 오차가 모두 동일하다 해도 모두 합산하게 되면
  데이터의 개수에 따라 오차의 정도가 달라지기 때문에, 이를 Normalize(정규화)하기 위함이다.

2️⃣ 위 과정을 Cost(=Loss) Function, $w^*$에 대해서 분리하면 아래와 같다.

2) 계산 예시

그럼 임의의 값을 $w$에 대입하고 $L(w)$를 계산해보자.

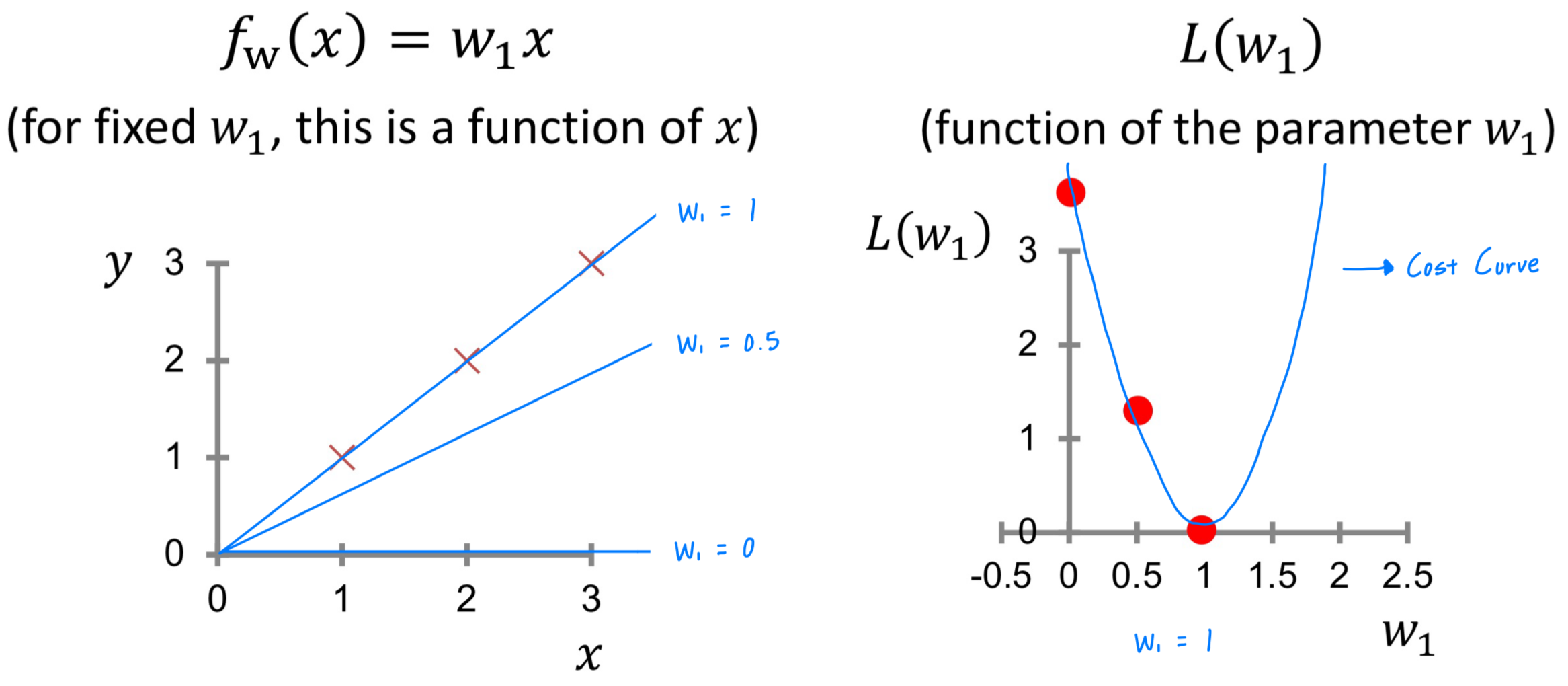
왼쪽 그림과 같이 Mapping Function은 $f_w(x) = w_1x$ 이고, 데이터는 $\{(0,0),\;(1,1),\;(2,2)\}$이다.
$w_1$ 에 0, 0.5, 1을 대입했을 때, $L(w_1)$을 계산해보자.

계산된 $L(w_1)$ 값을 오른쪽 좌표에 표시해보자.
무수히 많은 값을 $w$에 대입해보면, 오른쪽 좌표에 2차 함수 그래프와 같은 형태가 보이게 된다.
이렇게 $L(w)$의 값을 대입하여 나타나는 선을 Cost Curve라고 말한다.

3) Cost Function 종류

1️⃣ 좋은 Cost Function의 조건

• symmetric around 0 (0 주변에서 대칭이어야 한다.)
  만약 오차가 음수인 경우를 더 선호한다면, 양수/음수 오차를 모두 고려하지 않고 오차가 음수로 발생하는 방향으로 $w$를 선택하게 될 수 있다.
• Large mistake $\thickapprox$ Very large mistake (두 경우를 비슷하게 다루어야한다.)
  Large mistake와 Very large mistake를 다르게 고려하게 되면,
  Very large mistake(=Outlier)를 설명하기 위해 다른 값들을 제대로 설명할 수 없게 된다.

2️⃣ Cost Function의 종류

• MSE (Mean Squared Error, L2 Norm)
  • 가장 많이 사용 되는 비용 함수 중 하나이다.
  • Outlier vulnerable
  • $\mathrm{MSE}(f_w(x_n),y_n)\,=\,(f_w(x_n)-y_n)^2$
• MAE (Mean Absolute Error, L1 Norm)
  • $\mathrm{MAE}(f_w(x_n),y_n)\,=\,|f_w(x_n)-y_n|$
• Huber Norm
  • L1, L2 Norm의 장점들을 결합한 형태의 비용 함수이다.
  • Outlier robustness
  • $\mathrm{Huber}_{\delta}(f_w(x_n),y_n)\,=\, \begin{cases} \frac{1}{2}(f_w(x_n)-y_n)^2,& \text{for}\,|f_w(x_n)-y_n|\leq \delta\\ \delta \,\cdot\ (|f_w(x_n)-y_n|\,-\,\frac{1}{2}\delta) , & \text{otherwise} \end{cases}$
• 비용 함수별 형태
  특정 구간$(\geq\delta)$ 이후 부터는 L2 Norm 대비 Huber Norm의 Loss 증가가 완만함을 확인할 수 있고,
  이는 Huber Norm이 Outlier robustness function임을 보여준다.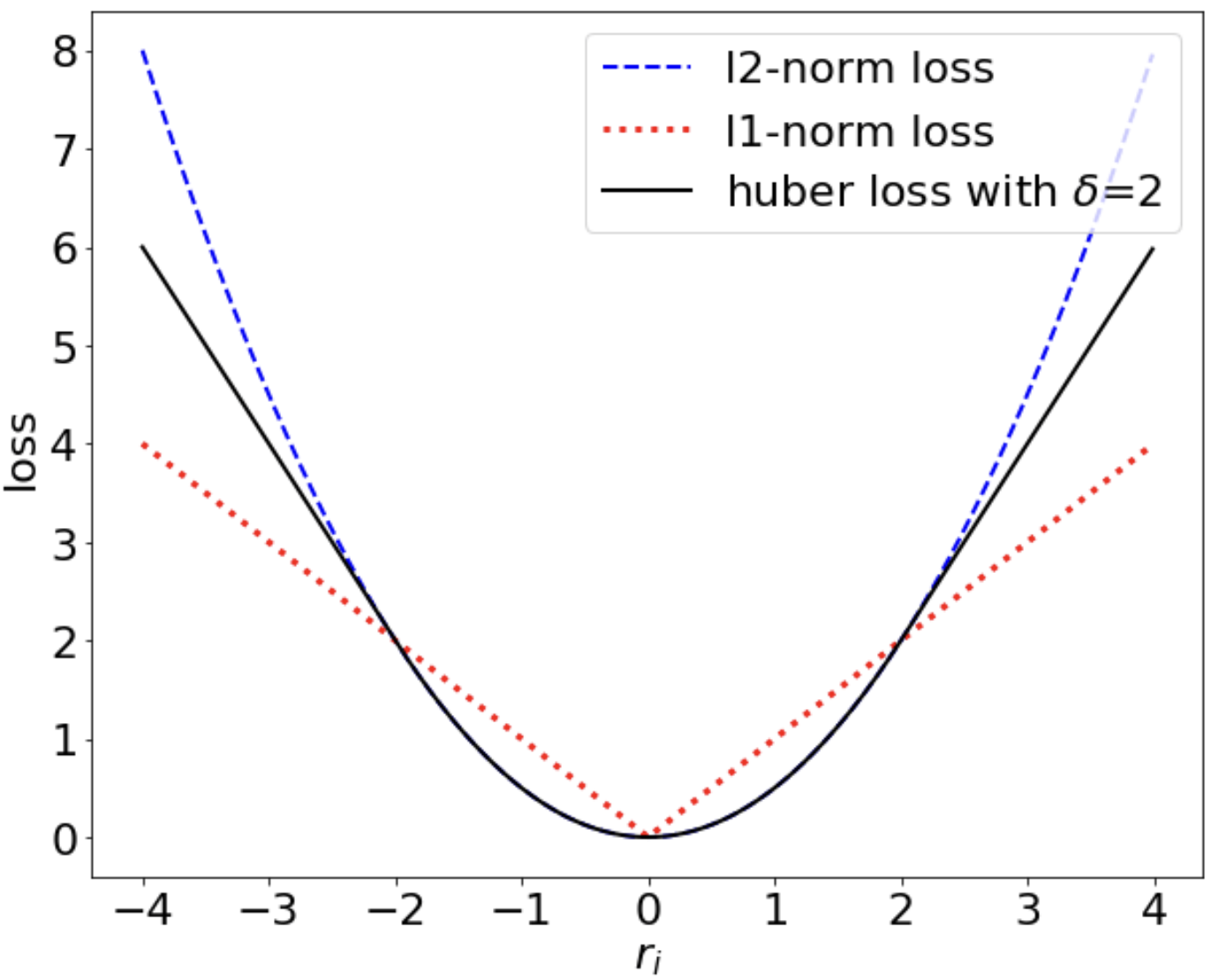

  

MSE는 이상치에 취약하지만 계산 비용이 낮다.
Huber Norm은 MSE/MAE 대비 이상치에 강건하지만 그만큼 계산 비용이 높다는 단점이 있다.
❗️Computer Cost ↔︎ Statistical property 는 서로 trade-off 관계이다.

또한 Cost Function 보다 Mapping Function의 복잡성을 늘리는 방법이
더 효과적이기 때문에 오늘날에는 MSE 함수를 많이 사용하고 있다.

3. Optimization(최적화)

우리는 어떻게 $L(w)$를 최소화하는 $w^*$를 찾을 수 있을까?
간단한 방법으로는 Grid Search가 있지만, $w$의 개수가 늘어날수록 계산량은 급격하게 증가한다.

1) Gradient Descent

그렇다면 우리는 다른 방법을 고민해봐야한다. 산에서 낮은 지점으로 내려갈 때를 떠올려보자.
길을 모를때는 경사진 곳을 따라 내려가다 보면 결국 낮은 지점으로 도착하게 될 것이다.
여기에서 착안 된 아이디어가 바로 Gradient Descent(경사 하강법)이다.

Gradient Descent는 산을 내려오듯이 경사진 곳으로 반복적하여 이동하여 최적점을 찾는 방법이다.
이 과정에서 방향, 이동거리, 시작점 총 3가지를 속성을 설계하게 된다.
그렇다면 어떻게 최적화 알고리즘을 설계하는지 하나 하나 살펴보자.

2) Gradient Descent의 속성

위에서 말했던 방향, 이동거리, 시작점은 Gradient Descent에서는 아래와 같이 말할 수 있다.

1️⃣ Negative Gradient : 방향
먼저 기울기에 대해서 정의해보면 어떠한 지점에서 가파른 정도를 뜻한다.
기울기가 가리키는 방향으로 이동한다면 값이 증가하겠지만, 반대 방향으로 이동하면 값이 감소할 것이다.

그렇다면 $L(w)$를 미분하여 기울기를 구하고 이에 대한 반대 방향으로 움직이면 $L(w)$가 감소하게 될 것이다.
우리는 $L(w)$를 최소화하는 $w$를 찾고 있기 때문에 $w$에 대해 $L(w)$를 편미분하게 되면
$L(w)$를 감소시키는 $w$의 방향을 알 수 있다. 이를 수식으로 나타내면 아래와 같다.

2️⃣ Learning Rate : 이동거리
다음으로 이동거리에 대해서 알아보자.
Gradient Descent에서는 다음 Step으로 얼만큼 이동할 것인지 정할 수 있다.
이를 Learning Rate라고 말하고 아래와 같이 수식으로 나타낼 수 있다.

Learning Rate($\alpha$)는 아래와 같은 특징이 있다.

• $\alpha$ 너무 작은 경우 : $L(w)$를 최소화하는 minimum에 수렴하기까지 오랜 시간이 걸린다.
• $\alpha$ 너무 큰 경우 : minimum에 수렴하지 못하거나, $L(w)$ 값이 발산하게 된다.

3️⃣ Initialization : 시작점
시작점을 결정하는 방법은 다양하지만, 여기에서는 Random Initialize를 한다고 가정하겠다.

3) Gradient Descent의 한계

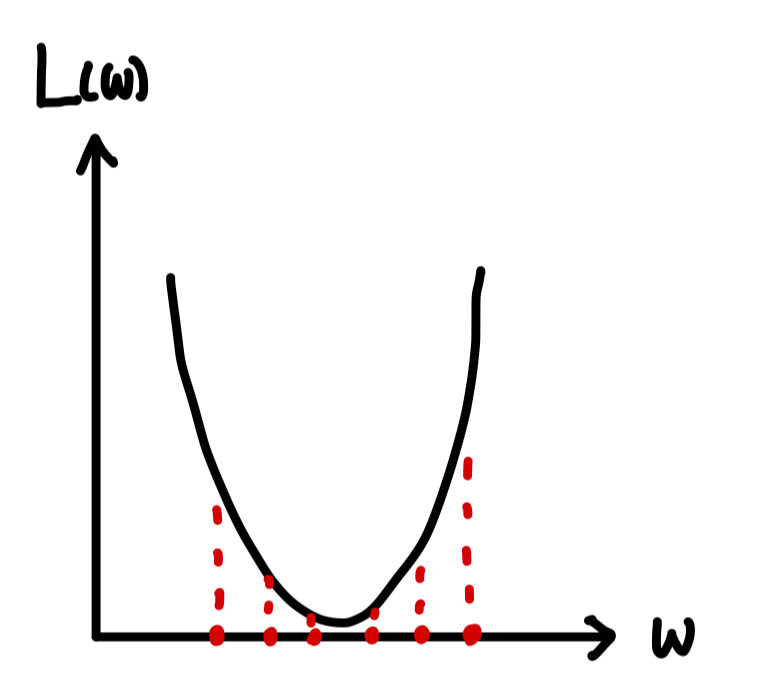
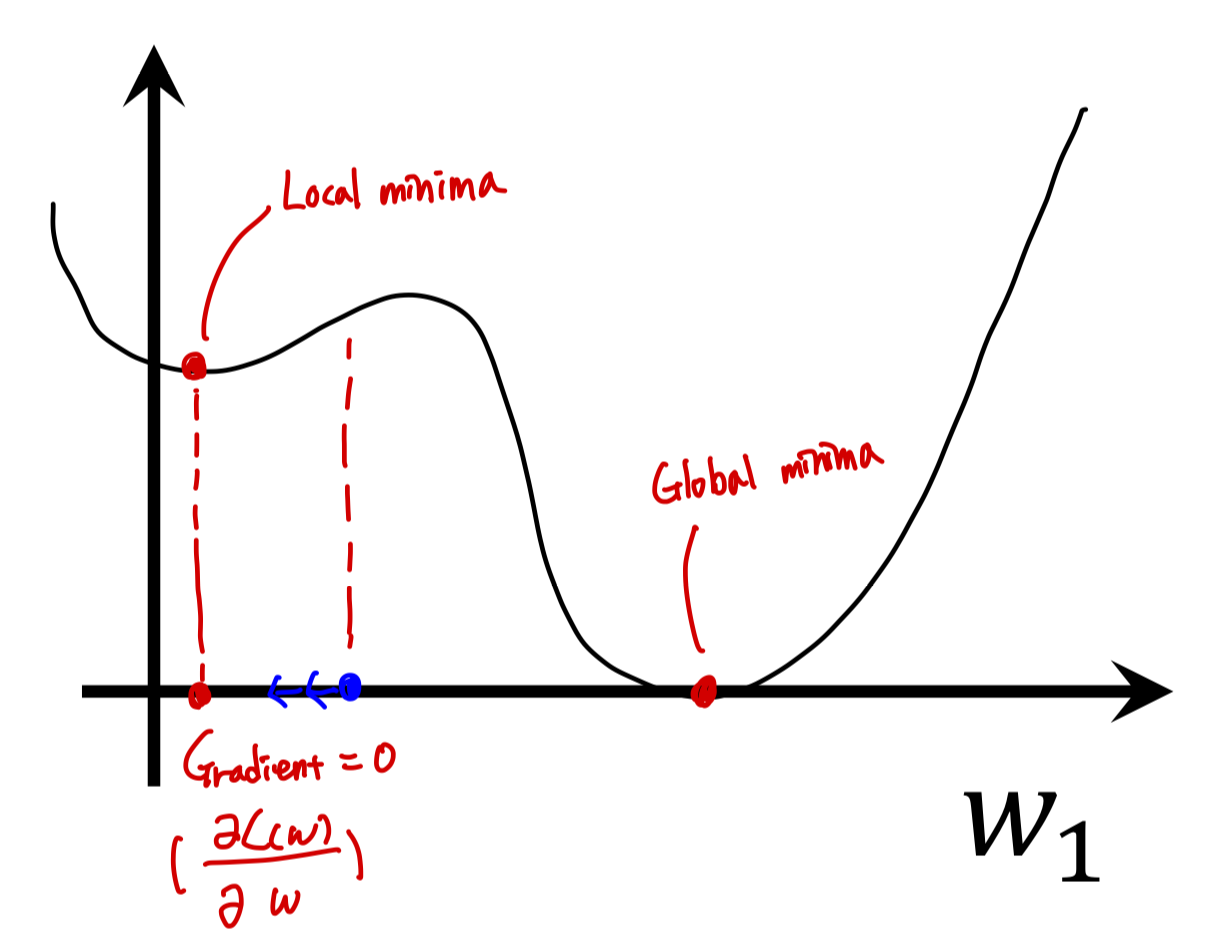
Cost Curve가 아래와 같은 형태일 때, 파란색 점에서 Initialize 되었다고 가정해보자.
Gradient Descent는 기울기의 반대 방향으로 이동하기 때문에, $w$는 왼쪽으로 이동할 것이다.
그렇다면 결국 $L(w)$는 Local minima에 수렴하게 되고 기울기가 0이 되어 더 이상 움직이지 않을 것이다.
이와 같이 Gradient Descent는 Initialization에 따라 Global minima를 찾지 못한다는 한계가 있다.

4. Linear Regression 종류

1) 단변량 선형회귀

단변량 선형회귀는 입력 인자 $X$가 1개인 경우이다.

2) 다변량 선형회귀

다변량 선형회귀는 입력 인자 $X$가 여러개인 경우이다.
다변량 선형회귀에서 최적의 $w$*를 찾기 위한 경사하강법의 과정을 아래 수식 처럼 나타낼 수 있다.

위의 편미분은 Chain Rule을 통해서 유도할 수 있는데, 그 과정은 아래와 같다.