이 글은 이소연 교수님의 자료구조 강의를 듣고 정리한 내용입니다.
스택(Stack)이란?
1️⃣ Stack의 정의
먼저 우리가 우리가 접시를 보관할때를 생각해보자. 일반적으로 가장 위에 접시를 쌓아두거나, 가장 위에 있는 접시를 꺼내온다. 접시의 이동이 한쪽에서만 이뤄지는데 이런 구조를 Stack이라고 말할 수 있다.
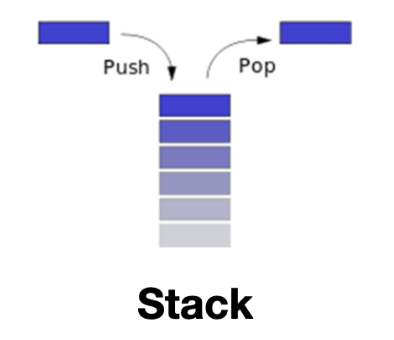
사전적인 의미로 설명하자면, Stack은 데이터를 한쪽 끝(top)에서만 삽입(push) / 삭제(pop)할 수 있는 선형 자료구조이고, 이는 가장 나중에 들어간 데이터가 가장 먼저 나오는 후입선출(Last In, First Out, LIFO) 구조를 따른다.
2️⃣ Stack, Queue, List
선형 자료구조의 대표적인 예로 Stack, Queue, List 3가지가 있으며, 임의의 위치에서 데이터를 삽입/삭제할 수 있는 List와 달리 Stack과 Queue는 아래의 그림과 같이 정해진 위치에서만 삽입/삭제 연산이 가능하다.

다음은 Stack, Queue, List의 특징들을 정리해놓은 표이다.
| 자료구조 | 삽입 위치 | 삭제 위치 | 특징 |
|---|---|---|---|
| List | 임의 위치 | 임의 위치 | 일반적인 자료구조 |
| Stack | Top | Top | LIFO 구조 |
| Queue | Rear | Front | FIFO 구조 |
LIFO(Last In, First Out) : 후입선출, 가장 나중에 들어간 데이터가 가장 먼저 나오는 구조
FIFO(First In, First Out) : 선입선출, 가장 먼저 들어간 데이터가 가장 먼저 나오는 구조
3️⃣ Stack의 추상 데이터 타입
Stack의 구성 요소와 필요한 연산들을 추상 데이터 타입을 통해 다음과 같이 정리할 수 있다.
- 객체 : n개의 원소들의 선형 리스트
- 연산
create(): Stack의 생성push(item): Stack의 top에 데이터를 추가pop(): Stack의 top에서 데이터를 제거하고 반환peek(): 삭제하지 않고 top 데이터를 반환is_empty(): Stack이 비어있는지 확인is_full(): Stack이 가득 찼는지 확인 (정적 구현 시)
Stack의 구현
그럼 이제 C언어를 통해 실제 Stack을 구현하는 방법에 대해서 알아보자.
Stack도 마찬가지로 배열을 이용하는 정적 구현과 연결리스트를 이용하는 동적 구현, 2가지 방법이 있다.
1️⃣ Stack의 정적 구현
배열을 이용해서 고정된 크기의 Stack을 생성할 수 있다.
이는 구현이 간단하다는 장점이 있지만, 불필요한 자원이 소모된다는 단점이 있다.
#define MAX 100
int stack[MAX];
int top = -1;
void push(int value) {
if (top < MAX - 1)
stack[++top] = value;
}
int pop() {
if (top >= 0)
return stack[top--];
return -1; // 오류 처리
}2️⃣ Stack의 동적 구현
연결리스트를 이용해서 가변되는 Stack을 생성할 수 있다.
이는 크기가 제한되지 않지만, 구현이 복잡하고 삽입/삭제에 시간이 오래 걸린다는 단점이 있다.
Stack의 응용
Stack은 함수 호출 / 수식 계산 / 되돌리기(Undo) 기능 등 다양한 분야에서 활용되며, 본 글에서는 대표적인 응용 사례 중 하나인 수식 계산에 대해 다뤄보고자 한다.
사람이 수식 계산을 하는 경우, 연산자의 우선 순위를 정하고 이에 따라 순서대로 연산을 진행하는 중위식(Infix Notation)을 주로 사용한다. 예시 : (((A/(B**C))+(D*E))-(A*C))
다만 컴퓨터가 수식 계산을 하는 경우, 중위식에서와 같이 전체 수식을 보고 우선 순위를 정하는 불필요한 과정을 제외하고 한번에 왼쪽에서 오른쪽으로 진행하며 계산할 수 있는 후위식(Postfix Notation)을 사용해서 계산하며 예시 : ABC*/DE*+AC*-, 여기에 Stack이 활용된다.
1️⃣ 후위식이란?
후위식(Postfix Notation)에 대해서 좀 더 자세히 알아보자.
먼저 후위식은 연산자(Operator)가 피연산자(Operand)의 뒤에 오는 수식 표기법으로, 이는 괄호 없이도 연산 순서를 명확히 알 수 있으며, 스택을 이용한 계산이 용이하다는 장점을 가진다.
예를 들어 중위식 3 / ( 5 + 4 )을 후위식으로 나타내면 3 5 4 + / 이다.
2️⃣ 후위식 변환
중위식에서 후위식으로 변환하는 방법은, ①중위식에 괄호를 친 뒤에 ②모든 연산자를 가장 가까운 괄호 뒤로 옮기고 나서 ③괄호를 지우면 후위식이 나오게 된다.

이때 Stack을 이용하여 중위식을 후위식으로 변환하는 알고리즘을 만들 수 있는데, 이는 다음과 같다.
- 피연산자는 출력
- 연산자는 Stack에 저장 (우선순위에 따라 pop 후 저장)
- 왼쪽 괄호는 무조건 push
- 오른쪽 괄호는 왼쪽 괄호가 나올 때까지 pop
알고리즘 2번 항목에서, 읽고 있는 연산자의 우선순위가 Stack Top의 연산자보다 우선순위가 높다면 Push 연산을 수행하고, 같거나 낮다면 Top의 연산자보다 우선순위가 높아질때까지 Pop 연산을 수행한다.
※ 연산자의 우선순위
연산자의 우선순위는 스택 안에서와 밖에서 다르게 적용되는데, 스택 밖 그러니까 입력 시의 우선순위는(Incoming Precedence, ICP)이며 스택 안에서의 우선 순위는(In-Stack Precedence, ISP)를 따른다. 기본적으로괄호 ()>지수 ^>곱셉, 나눗셈 * />덧셈,뺄셈 + -순으로 우선순위가 높지만, ICP의 경우 괄호의 우선순위가 가장 낮다.
3️⃣ 후위식 계산
후위식 계산의 경우, 괄호와 우선순위가 필요 없고 Stack만을 사용하여 수식을 왼쪽부터 오른쪽으로 순차적으로 읽으면서 계산할 수 있다.
이때 시간복잡도, 공간복잡도는 모두 O(n)이다.
계산 시의 알고리즘의 순서는 다음과 같다.
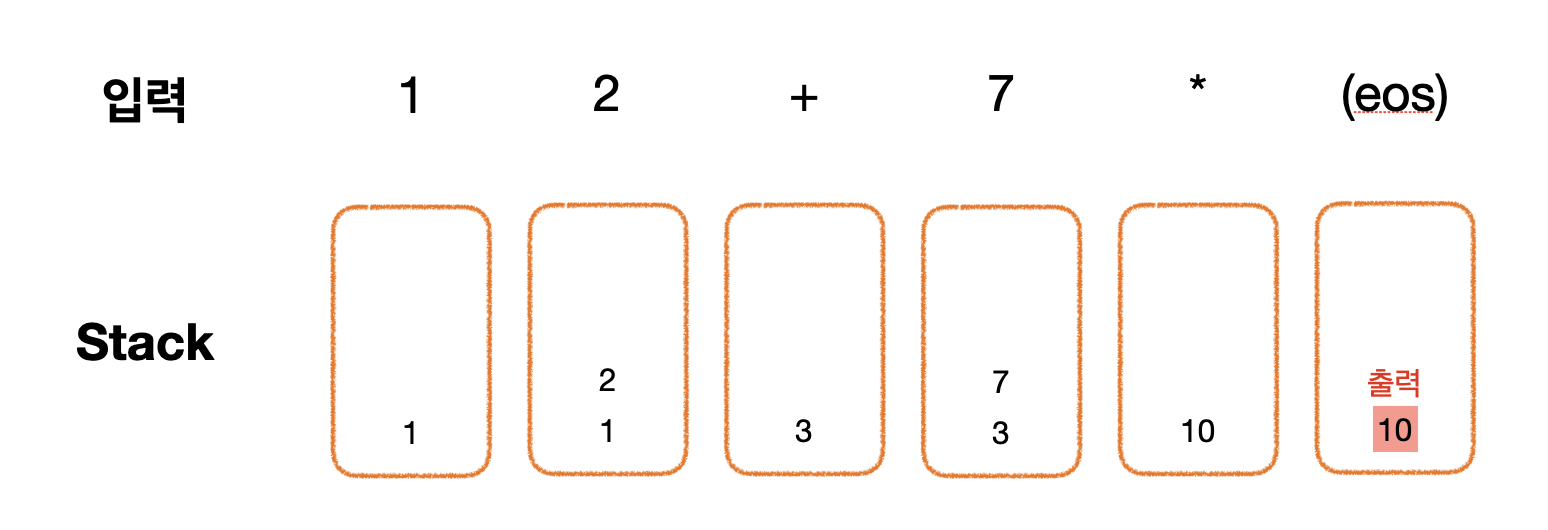
- 피연산자는 Stack push
- 연산자가 나오면 피연산자 2개 pop, 계산 후 결과는 Stack push
- 모든 입력이 끝났을 때의 Stack top을 결과로 출력
만약 1 2 + 7 * 이라는 후위식이 주어졌을때, 이를 계산하는 과정 및 Stack의 변화는 아래와 같다.