확률과 통계 #2 Measure Theory

이 글은 최성준 교수님의 확률과 통계 강의를 듣고 정리한 내용입니다.

---

확률을 이해하기 위해 앞서 확률의 근간이 되는 Set Thoery(집합론)에 대해서 다뤘고,
본 글에서는 앞에서 정의했던 Set들을 측정하기 위한 Measure Theory(측도론)에 대해 다루고자 합니다.

---

Measure

먼저 Measure Theory에서 Measure란 무엇일까? 사전적인 정의는 다음과 같다.

전체 집합 $U$가 주어졌을 때, 각각의 $U$의 부분집합을 양수로 할당하는 것을 measure라고 한다.

Give a universal set $U$,
a measure assigns a non-negative real number to each subset of $U$

즉, Measure는 subset → 양수(몸무게 or 길이 등)으로 매핑하는 set function으로 볼 수 있다.

여기서 눈여겨봐야할 점은 Measure의 입력이 element가 아닌 subset이라는 것인데,
만약 우리가 어떤 몸무게를 측정한다고 가정해보자.

그럼 우리는 1명의 몸무게만 측정하는게 아니라 2명, 3명처럼 여러명의 몸무게를 측정할 수 있어야 한다.
다시 말해 Measure는 개별적인 element가 아니라 set을 입력 받을 수 있어야 하기 때문에,
정의에서도 subset이라고 말하고 있는 것을 알 수 있다.

---

$\sigma$-field

위의 정의에 따라서 Measure는 subset을 입력으로 받고,
이는 다시 말해 Measure Function의 Domain이 subset으로 구성되어 있다고 할 수 있다.

이러한 Measure Function Domain이 가지는 특성으로 Domain은 항상 $\sigma$-field 라고 할 수 있는데,
여기서는 $\sigma$-field 가 무엇이고 어떤 특징이 있는지 알아보고자 한다.

1️⃣ $\sigma$-field 공리

먼저 $\sigma$-field $\mathscr{B}$는, 아래의 3가지 공리(Axioms)를 만족하는 부분 집합으로 이루어진 집합을 의미한다.
또한 $\sigma$-field는 $\sigma$-algebra 로 불리기도 한다.

Axioms of $\sigma$-field

1. $\varnothing \in \mathscr{B}$
   • an empty set is included
   • $\sigma$-field는 공집합 $\varnothing$을 포함되어야 한다.
2. $B \in \mathscr{B} \Rightarrow B^c \in \mathscr{B}$
   • closed under set complement
   • $\sigma$-field는 Complement(여집합)에 닫혀 있어야 한다.
     이후 확률론에서 사건이 일어난다면($B$), 일어나지 않는 경우($B^c$)도 고려해야함을 의미한다.
   • $U=\{\{a,b,c\}\} \Rightarrow \{a,b,c\} \in \mathscr{B},\;\;\{a,b,c\}^c=\{\varnothing\} \in \mathscr{B}$
3. $B_i \in \mathscr{B} \Rightarrow \bigcup_{i=1}^{\infty} B_i \in \mathscr{B}$
   • closed under countable union
   • $\sigma$-field는 원소들의 Union(합집합)에 닫혀 있어야 한다.
     이후 확률론에서 여러 사건이 결합된 결과도 고려해야함을 의미한다.
   • $\{a\},\;\{b\} \in \mathscr{B}, \;\; \{a,b\} \in \mathscr{B}$

만약 전체 집합 $U=\{a,b,c\}$ 가 주어졌을때 위의 공리에 따른 $\sigma$-field 를 구한다면,
가장 Coarse한 $\sigma$-field 는 $\{ \varnothing, \{a,b,c\}\}$ 이고, 가장 Fine한 $\sigma$-field 는 power set $2^U$ 일 것이다.
※ power set은 주어진 집합의 모든 부분 집합으로 이루어진 집합이기 때문이다.

위의 예시를 통해서, $\sigma$-field 는 power set 뿐만 아니라 여러 집합이 존재할 수 있음을 알아두자.

2️⃣ $\sigma$-field 특징

위의 공리를 만족하는 집합인 $\sigma$-field $\mathscr{B}$ 에는 아래와 같은 특징이 존재하며,
집합 $\mathscr{A}$ 에 의해 만들어진 $\sigma$-field 를 $\sigma(\mathscr{A})$ 와 같이 표현한다.

Properties of $\sigma$-field

1. $U \in \mathscr{B}$
   • the entire set is included (공리 1,2에 따른 성질)
2. $B_i \in \mathscr{B} \Rightarrow \bigcap_{i=1}^{\infty} B_i \in \mathscr{B}$
   • closed under countable intersection
   • $\sigma$-field는 원소들의 Intersection(교집합)에 닫혀있다.
   • $\{a,b\},\;\{b,c\} \in \mathscr{B}, \;\; \{b\} \in \mathscr{B}$
3. $\text{Power set}\;2^U \Rightarrow \sigma\text{-field}$
   • 어떠한 집합의 Power set은 가장 Fine한 $\sigma$-field 이다.
4. $\mathscr{B}$ is either finite or uncountable, never denumerable.
   • $\mathscr{B} = 2^\mathscr{A}$, $\sigma$-field 는 결국 다른 어떤 집합의 power set 형태로 표현할 수 있다.
   • $\mathscr{B}$ is finite : 유한 집합의 power set은 유한 집합이다.
   • $\mathscr{B}$ is uncountable : 무한 집합의 power set은 셀 수 없는 집합이다.
     $|\mathbb{R}|=2^{\aleph_0}$(이전 글)으로, 자연수(denumerable) 집합의 power set은 uncountable 이다.
5. If $\mathscr{B}$ and $\mathscr{C}$ are $\sigma$-fields, then $\mathscr{B} \cap \mathscr{C}$ is a $\sigma$-field, but $\mathscr{B} \cup \mathscr{C}$ is not.
   • $\sigma$-field의 교집합은 $\sigma$-field 이지만, 합집합은 그렇지 않다.
   • $\mathscr{B} = \{\varnothing, \{a\}, \{b, c\}, \{a, b, c\}\} \quad\text{and}\quad \mathscr{C} = \{\varnothing, \{a, b\}, \{c\}, \{a, b, c\}\}$
   • $\mathscr{B} \cap \mathscr{C} = \{\varnothing, \{a, b, c\}\}$ is a $\sigma$-field.
   • $\mathscr{B} \cup \mathscr{C} = \{\varnothing, \{a\}, \{c\}, \{a, b\}, \{b, c\}, \{a, b, c\}\}$ is not a $\sigma$-field.
     ※ $\{a, c\}$ is not included.

A $\sigma$-field is designated to define a measure on a set.
이렇게 정의한 $\sigma$-field 는 결국 Measure Function을 정의하기 위해 설계된 것이다.

Function은 관측 가능한 모든 Domain에 대해 정의되어야 하기 때문에,
$\sigma$-field를 통해 Domain의 범위에 대해 정의하고 Measure Function을 Mapping 시키는 것이다.

If an element is not inside the $\sigma$-field, the it cannot be measured.
다시 말해, $\sigma$-field에 없는 원소는 Measure Function을 Mapping, 즉 관측할 수 없다.

---

Measure space

위에서 정의했던 $\sigma$-field $\mathscr{B}$ 를 통해
아래와 같이 Measure를 포함해 Measureable Space, Measure Space에 대해 정의할 수 있으며,
이는 Probability(확률)에서 확률을 계산하는 함수와 전체 사건 공간으로 활용된다.

1️⃣ Measure 관련 용어

1. Measurable Space (측정 가능한 공간)
   • 전체 집합 $U$와 $\sigma$-field 로 이루어진 공간 $(U, \mathscr{B})$
2. Measure (측도)
   • Measurable Space $(U, \mathscr{B})$의 set function, Measure $\mu:\;\mathscr{B} \rightarrow [0, \infty]$
   • $\mu(\varnothing) = 0$
   • $\mu\left(\bigcup_{i=1}^{\infty} B_i\right) = \sum_{i=1}^{\infty} \mu(B_i) \quad\dots\quad(\text{disjoint set}\;B_i\;\text{and}\;B_j)$
     countable additivity 서로소 집합의 합집합에 대한 측도는 각 집합의 측도의 합과 같다.
3. Measure Space (측도 공간)
   • Measurable Space, Measure가 함께 정의된 공간, Measure Space$(U, \mathscr{B}, \mu)$
4. Probability(확률)
   • $\mu(U)=1$, 전체 사건의 확률이 1로 나타나는 Measure (normalized measure)

2️⃣ Measure 특징

추가로 Measure Function이 가지는 특징에 대해서 조금 더 살펴보자.

① Countable additivity
먼저 Countable additivity(가산 가능한 덧셈)이란,
위에서 설명한 것과 같이 서로소 집합의 합집합과 각 집합의 측도의 합은 같다는 것을 의미한다.

이는 아래 그림과 어떤 공간의 면적은 각각 나눠진 공간의 면적의 합과 같음을 의미하며(/w 적분),
확률에서 독립 사건들의 합을 통해서 전체 사건의 합을 구할 수 있음을 의미한다.

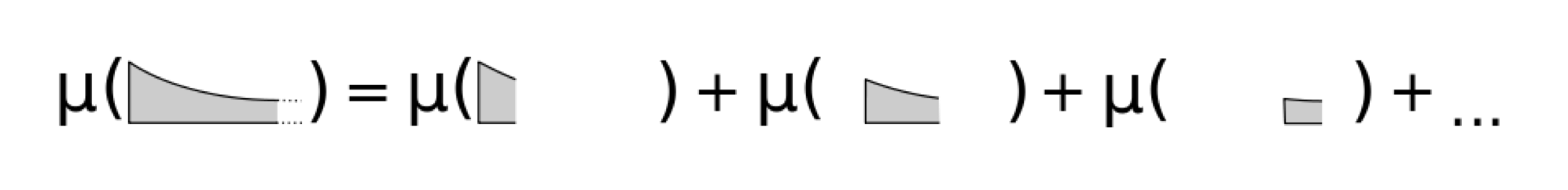
② Monotonicity
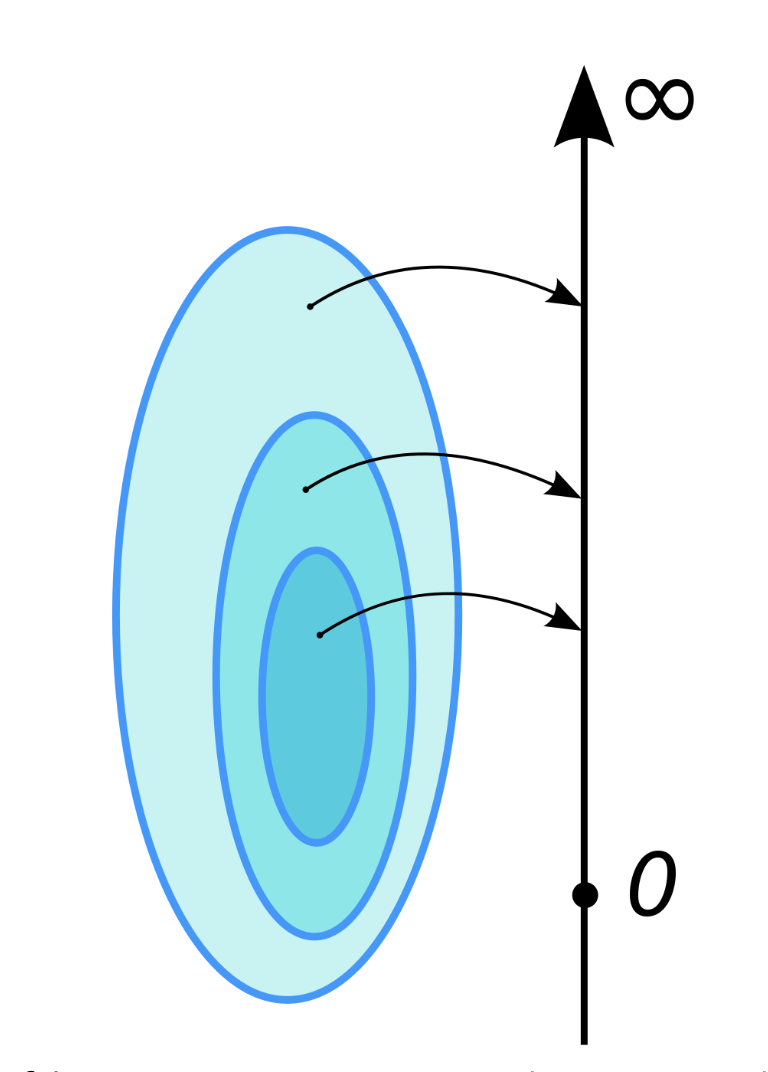
다음으로 Monotonicity(단조성)이란,
집합 A가 집합 B의 부분집합이면, A의 측정값이 B의 측정값보다 작거나 같아야 한다는 성질을 말한다.

또한 위에서 다뤘듯이, 공집합 $\varnothing$의 측정값은 0이다.

---

이렇게 확률에 대해 살펴보기 위해
본 글의 Measure Theory(측도론)과 이전 글의 Set Theory(집합론)에 대해서 살펴보았다.

다음 글에서는 본격적으로 확률이 어떻게 정의되는가에 대해서 살펴보려고 한다.