확률과 통계 #1 Set Theory

이 글은 최성준 교수님의 확률과 통계 강의를 듣고 정리한 내용입니다.

---

앞으로 이어질 글에서는 확률을 정의할 때, 단순히 확률을 빈도주의 관점에서 얘기하는 것이 아니라
Random Variable / Process를 통해 실생활 내 현상들을 일관성 있는 확률로 정의하고자 한다.

그러기 위해서 먼저 Set Theory(집합론), Measure Theory(측도론)에 대해 알아야 하는데,
본 글에서는 Set Theory에 대해 다루고자 한다.

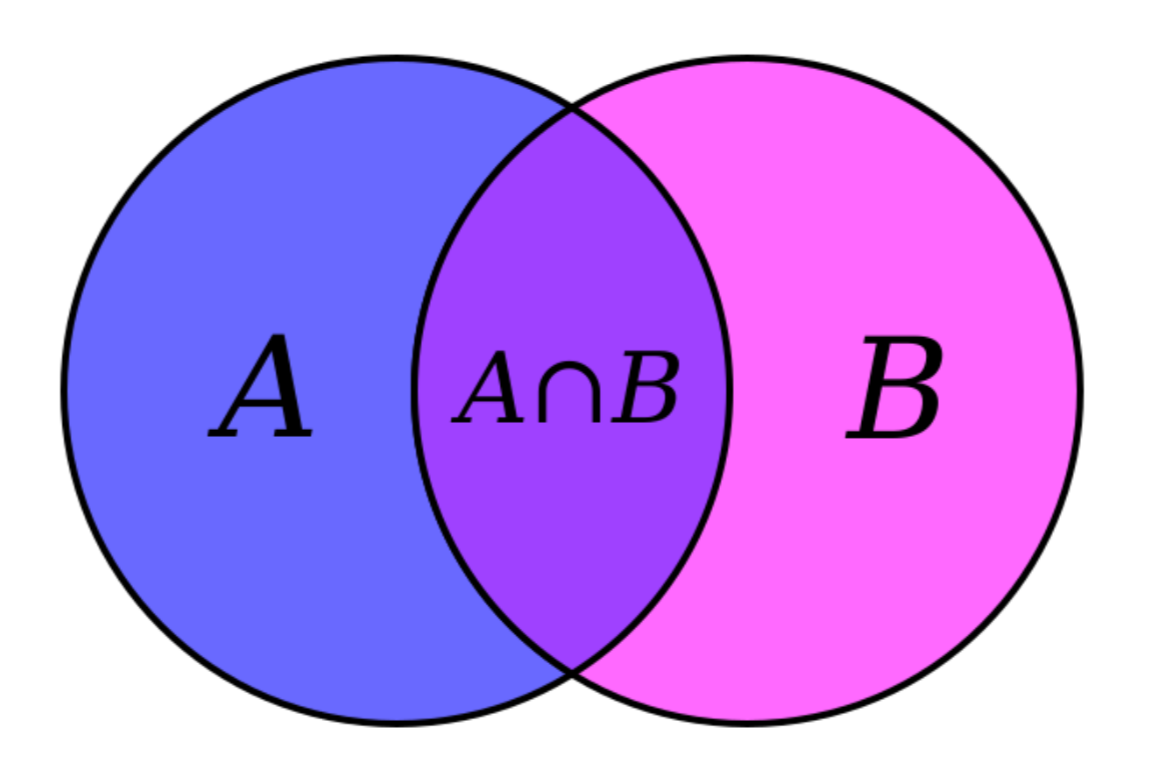
용어 및 개념

먼저 Set Theory에서 주로 쓰이는 용어 및 개념부터 알아보자.
Set Theory에서 사용되는 기본적인 용어와 개념인데, 중고등 수학때 다뤘던 개념도 있어 간단하게 정리했다.

1️⃣ 주요 용어

기본 용어	설명	예시
set, 집합	객체의 모음	$\{1, 2, 3, 4, 5\}$
element, 원소	집합의 구성 요소	$1 \in \{1, 2, 3\}$
subset, 부분 집합	{a, b}는 {a, b, c}의 부분 집합
universal set, 전체 집합	모든 대상을 원소로 포함하는 집합	{x, y, z}는 {x, y}와 {y, z}의 전체 집합이다
disjoint sets, 서로소 집합	공통 원소가 없는 집합	$A ∩ B = \varnothing$
partition of A, A의 분할	원소들이 겹치지 않는 부분 집합으로 분류	$A = \{1, 2, 3\} \\ \text{partition of A} : \{\{1,2\}, \{3\}\}$
Cartesian product, 데카르트 곱	$A \times B = \{(a,b) : a \in A, b \in B \}$	$A = \{1, 2\}, B=\{3,4,5\} \\ A \times B = \{ (1,3), (1,4), \cdots,(2,5) \}$
power set, 멱 집합 ($2^A$)	집합의 모든 부분 집합으로 이루어진 집합	$2^A = \{ \varnothing, \{1\}, \cdots,\{1,3\}, \{1,2,3\} \}$

2️⃣ 주요 개념

• Cardinality
  • Cardinality(기수)는 집합에 포함된 원소의 개수를 의미하며, $|A|$와 같이 표현한다.
    만약 $|A| = n$ 이라면, 멱 집합 power set의 cardinality는 $|2^A| = 2^n$ 이다.
  • 또한 집합 간에 일대일 대응 관계를 가지는 경우, Cardinality는 같다고 말할 수 있다.

• Cardinality에 따른 집합의 종류
  Cardinality에 따라 집합을 5가지 속성으로 나타낼 수 있고, 1개의 집합이 여러 속성을 가질 수 있다.
  (속성 : Finite, Infinite, Countable, Uncountable, Denumerable)
  • Finite / Infinite : 원소의 개수가 유한 / 무한한지에 따라서 구분할 수 있다.
  • Countable
    : 자연수의 집합 또는 부분 집합과 일대일 대응 관계를 가지는 경우를 말한다.
  • Denumerable
    : 다르게 표현하면 Countably infinite으로, 원소가 무한하지만 셀 수 있는 집합을 의미한다.
      자연수 전체 집합도 여기에 포함되며, $|\mathbb{N}| = \aleph_0$(aleph-null)와 같이 표현한다.
  • Uncountable
    : 말 그대로 셀 수 없는 집합을 의미하며, [0, 1] 사이의 실수와 같은 집합이 여기에 포함된다.
      즉 실수 전체 집합 $\mathbb{R}$ 도 포함하며, $|\mathbb{R}| = c\text{ (continuum)} = 2^{\aleph_0}$와 같이 표현한다.

집합 간 사상(Mapping)

집합 간 사상(Mapping or function)은 집합 간의 원소를 대응 시키는 것을 의미하며,
기호로는 $f : U \rightarrow V$ 와 같이 나타낼 수 있다.

1️⃣ 주요 용어

집합 간 사상에서 사용되는 주요 용어는 아래와 같다.

기본 용어	설명	예시
domain, 정의역	Mapping에서 입력으로 주어지는 집합	$U$
codomain, 공역	Mapping을 통해 대응시키고자 하는 집합	$V$
image, 상	정의역의 원소들에 Mapping 되는 공역의 원소들	$f(A) = \{f(x) \in V : x \in A \}$
range, 치역	정의역의 모든 원소에 Mapping 되는 공역 원소들의 집합	$f(U)$
inverse image, 역상	pre-image(원상)이라고도 하며, range의 반대 개념	$f^{-1}(B) = \{x\in U:f(x) \in B\}$

2️⃣ Mapping의 유형

집합 간의 원소를 대응 시키는 Mapping은 대응되는 방식에 따라 아래의 그림과 같이 나눌 수 있다.
마지막 그림은 정의역의 원소가 공역의 여러 원소와 대응되기 때문에 Mapping(function)이라 할 수 없다.

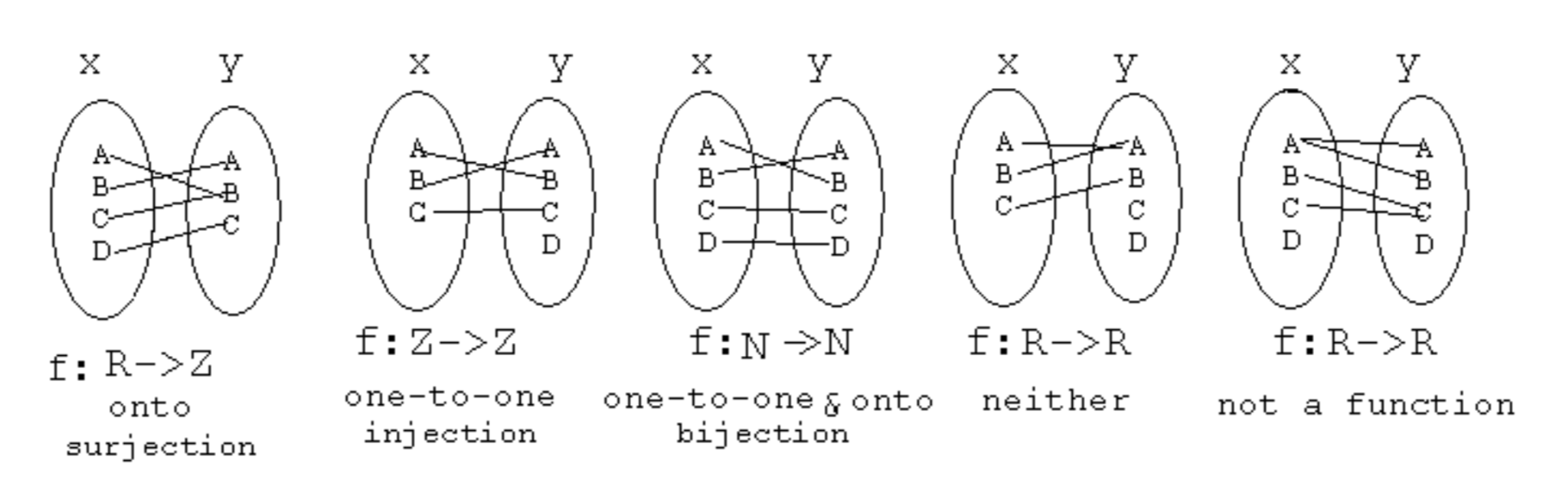
1. 전사 함수 (onto, surjection)
   공역과 치역이 같은 경우를 말하며, $|X| \geq |Y|$ 이라는 성질을 가진다.
2. 단사 함수 (one-to-one, injection)
   정의역 원소가 다른 경우, 이에 대응되는 공역의 원소도 다른 경우를 의미한다.
   또한 $|X| \leq |Y|$ 이라는 성질을 가진다.
3. 전단사 함수 (bijection)
   정의역과 공역을 중복 없이 일대일로 대응 시키는 경우를 말하며, $|X| = |Y|$ 이라는 성질을 가진다.
   또한 이름에서도 알 수 있듯이 전사/단사 함수 조건을 모두 만족하며,
   일대응 대응(one-to-one correspondence) 또는 Invertible 이라고도 말한다.

확장 공리(외연 공리)

위에서 집합의 정의와 집합 간의 관계를 다뤘는데, 이 집합들이 같다고 말하려면 무엇을 비교해봐야할까?
이를 위한 것이 바로 확장 공리(Axiom of extensionality)이다.

확장 공리에서는 집합 $A, B$ 가 동일한 원소를 갖는 경우에 2개의 집합 $A, B$가 서로 같다고 말한다.

다만, 이러한 공리로는 Infinite / Uncountable 집합 간의 비교는 할 수 없다.

따라서 확장 공리에서 말하고 있는 집합의 원소를 하나하나 비교하는 것이 아닌
집합 간의 Cardinality가 같음을 확인하는 경우도 있는데, 여기에 대한 내용을 좀 더 다뤄보고자 한다.

1️⃣ 자연수와 정수 집합

자연수 전체 집합 $\mathbb{N}$과 정수 전체 집합 $\mathbb{Z}$이 존재할 때, 2개 집합의 Cardinality는 같다고 말할 수 있을까?
결론부터 먼저 말하자면, 2개 집합의 Cardinality는 같다.

직관적으로 생각해보면, 정수 전체 집합의 Cardinality가 2배 정도 될 것 같은데..
2개 집합 모두 Denumerable, 즉 무한한 함수이기 때문에 이를 직접 계산할 수는 없다.

집합론에서는 2개 집합 사이에 bijective mapping(전단사함수)가 존재한다면,
Cardinality가 같다고 말하는데 이를 통해서 우리는 $|\mathbb{N}| = |\mathbb{Z}|$를 증명할 수 있다.

아래와 같은 mapping(function)이 존재한다고 가정해보자.

그렇다면 (1 → -1), (2 → 1), (3 → -2), (4 → -2) $\cdots$ 와 같이 무한히 일대일 대응 되는 관계를 알 수 있다.
이를 통해서 우리는 자연수 전체 집합 $\mathbb{N}$과 정수 전체 집합 $\mathbb{Z}$ 사이에 bijective mapping을 찾아내고
2개 집합의 Cardinality가 같다고 말할 수 있으며, 정수 전체 집합 $\mathbb{Z}$도 denumerable set임을 알 수 있다.

2️⃣ 실수 1차원과 실수 2차원 집합

그렇다면 실수에서는 어떻게 적용할 수 있을까?

위와 같이 2개 실수 집합이 존재한다면 직관적으로 생각해봤을때 $|A| = 2 |B|$라고 생각할 것이다.
하지만 자연수/정수 집합과 마찬가지로 이 2개 집합의 Cardinality도 같다.

실수를 이진법을 통해서 나타내고, $A, B$의 원소를 아래와 같이 나타내보자.

그렇다면 A에 속하는 어떤 원소가 주어지면, 여기에 대응되는 B의 원소를 무한히 찾아낼 수 있는
일대일 대응 관계를 찾아낼 수 있을 것이다.

이를 통해서, 위와 같이 $|A| = |B|$ 임을 증명할 수 있다.

Etc...

1️⃣ 칸토어의 대각선 논법

칸토어의 대각선 논법(Cantor's Diagonal argument)은,
실수 집합의 크기 $|\mathbb{R}|$ 가 자연수 집합의 크기 $|\mathbb{N}|$ 보다 더 크다는 것을 증명하는 논법이다.

이는 이진법으로 이루어진 실수를 자연수와 무한히 대응시켜도,
결국 대응되는 실수의 대각성분 보수값으로 이루어진 새로운 실수가 생기기 때문에,
실수 집합은 자연수 집합과 대응되지 않는, 즉 셀 수 있는 집합이 아닌 셀 수 없는 집합임을 말한다.

2️⃣ 실수의 Cardinality

우리는 실수의 Cardinality, 예를 들어 0과 1 사이의 모든 실수의 개수를 어떻게 알 수 있을까?

위의 Cardinality에 따른 집합의 종류에서, 실수 집합 $\mathbb{R}$은 Uncountable 집합이며
$|\mathbb{R}| = c = 2^{\aleph_0}$ 이라고 설명했었는데, 그 이유에 대해서 다뤄볼 것이다.

0과 1 사이의 실수에 대해 이진법을 통해 표현하면 아래와 같이 나타낼 수 있다.

여기서, 하나의 원소 $x$에 포함된 $d_{i,j}$의 개수는
자연수 집합의 개수 $\aleph_0$와 같고, $d$는 이진법이기 때문에 $|d_{i,j}| = 2$라고 말할 수 있다.

즉 다시 말해, 실수 집합의 원소는 $|d_{i,j}|^{\aleph_0} = 2^{\aleph_0}$ 라고 말할 수 있으며 이를 $c$라고 표현한다.