[확률과 통계] 정규분포

본 글은 칸아카데미의 미적분 - 확률과 통계에 대해서 공부하고 정리한 글입니다.

1. 정규분포

정규분포는 데이터가 평균을 중심으로 대칭적으로 분포하는 확률 분포를 말하며,
중심이 평균($\mu$)이고, 분포의 폭은 표준편차($\sigma$)에 의해 결정된다.

아래의 이미지는 다양한 정규 분포를 나타내며,
이 중 빨간색 정규분포($\mu=0,\,\sigma=1$)인 정규분포를 표준정규분포라고 한다. (※ 이미지 원본)

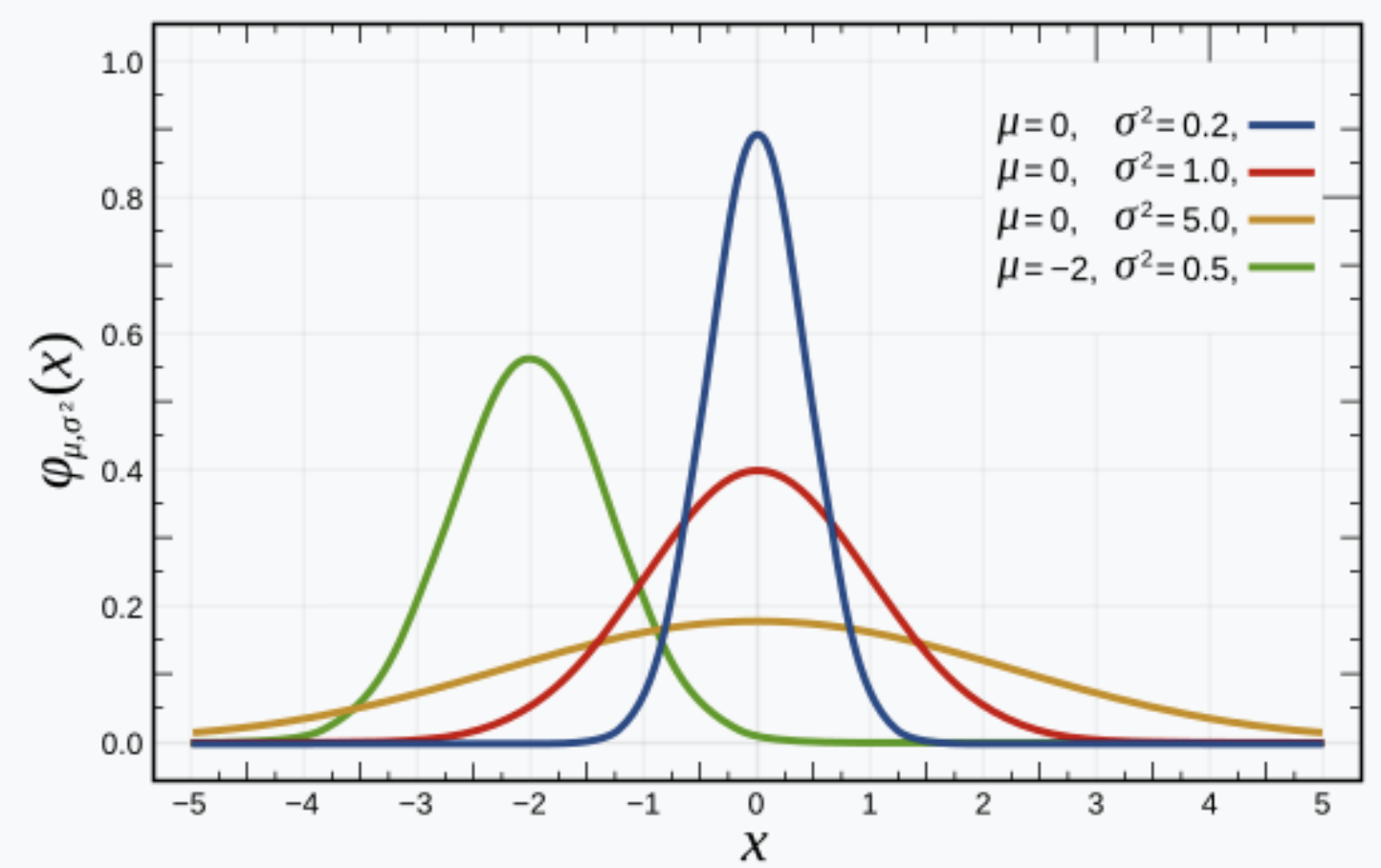
1-1. 정규분포와 표준편차의 관계

표준편차는 평균으로부터 데이터가 얼마나 퍼져 있는지를 나타내는 통계량인데,
정규분포에서는 데이터의 일정 비율이 특정 표준편차 범위 내에 존재한다는 특징을 가진다.

• 1σ 범위 (68%): 평균에서 ±1표준편차 범위 내에 전체 데이터의 약 68%가 존재
• 2σ 범위 (95%): 평균에서 ±2표준편차 범위 내에 전체 데이터의 약 95%가 존재
• 3σ 범위 (99.7%): 평균에서 ±3표준편차 범위 내에 전체 데이터의 약 99.7%가 존재

2. Z-Score

Z-Score(표준 점수)는 데이터가 평균으로부터 얼마나 떨어져 있는지를 표준편차 단위로 나타낸 값이다.
Z-Score를 사용하면 정규분포에서 데이터가 평균으로부터 얼마나 떨어져 있는지 확인할 수 있으며,
아래의 수식을 통해서 구할 수 있다.