수학

선형대수학 - 벡터와 공간 정리

순열과 조합 정리

조건부 확률과 베이즈 정리

1. 스칼라와 벡터 스칼라(Scala) : 크기(또는 양)만으로 표현되는 값 기호 : $$x, y$$ 예시 : 온도, 시간, 질량 벡터(Vector) : 크기와 방향으로 표현되는 값 기호 : $$\vec{x}, \vec{y}, \bm{x}, \bm{y}$$ 예시 : 속도, 힘, 변위 2. 벡터 연산 벡터도 동일하게 산술 연산이 가능하다. ...

1. 선형 결합(Linear Combination) 벡터의 스칼라배들이 합으로 연결되어 있는 상태. 벡터 집합 $V = \{\vec{v1}, \vec{v2}, \cdots, \vec{vn}\}$ 와 스칼라 $a1, a2, \cdots, an$ 의 선형 결합은 $a1\vec{v1}, a2\vec{v2}, \cdots, an\vec{vn}$ 으로 나타낸다. ...

벡터의 곱하기는 2가지 종류가 있다. 벡터의 내적과 외적, 2가지 종류에 대해서 정리해보고자 한다. 1. 벡터의 내적 내적(dot product) : 벡터의 방향을 고려하여 수처럼 곱하는 방식이며, 기호 $\cdot$ 를 사용하고 결과는 스칼라이다. 교환 / 결합 / 분배 법칙의 적용이 가능하다. 벡터의 내적은 다음과 같이 계산한다. $$\vec{a} \...

행렬의 연산 중 덧셈 / 스칼라 배는 벡터에서의 연산 방법과 동일하지만, 행렬과 벡터의 곱셈은 다른 방식으로 계산된다. 본문에서는 행렬과 벡터의 곱셈하는 방법과, 열벡터 / 행벡터로 나누어 계산하는 방법에 대해서 설명하고자 한다. 1. 행렬의 곱셈 $\textbf{A}_{m \times n} \,\times\, \vec{x}$ 를 계산할 때, $\vec...

행렬의 영공간과 열공간의 정의와 특징들에 대해 설명해보고자 한다. 1. 영공간 (Null Space) 영공간의 정의 영공간(Null Space) : $\textbf{A}\vec{x} = \vec{0}$ 을 만족하는 $\vec{x}$의 모든 집합 행렬 $\textbf{A}_{m \times n}$ 의 영공간 $$= N(\textbf{A}) = \begi...

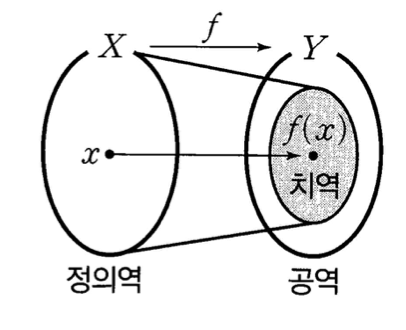
1. 선형 변환이란? 주요 용어의 정의 정의역 (Domain) : 입력되는 값(선형 변환에서는 벡터)의 집합 공역 (Co-Domain) :선형 변환을 통해 생성 가능한 모든 출력 벡터의 집합 치역 (Range) : 정의역의 선형 변환을 통해 생성 가능한 실제 출력 벡터의 집합 $$\,$$ 선형 변환 (Linear Transformat...

1. 단위 벡터 (Unit vector) 단위 벡터의 정의 벡터의 크기(norm)가 1인 벡터를 단위 벡터(unit vector)라고 한다. ※ 벡터의 크기 norm $=\, ||\vec{v}|| \,=\, \sqrt{v1^2 + v2^2 + \dots + v_n^2}$ 단위 벡터 구하기 주어진 벡터 $\vec{v}$ 와 같은 방향의 단위 벡터를 $\...

1. 항등함수와 역함수 항등함수 (Identify function) 집합 내의 모든 원소를 원소 자체에 매핑하는 함수를 말한다. $$ \textbf{I}_x: \textbf{X} \longmapsto \textbf{X} \quad\dots\quad \textbf{I}_x(a) = a $$ 역함수 (Inverse function) 기존 함수의 변환값을 반대로...

1. 기약행사다리꼴과 역행렬 행렬 $\textbf{A}_{m\times n}$이 역행렬을 가지려면, $Rank(\textbf{A}) =n=m$ 이어야 한다. 이는 $rref(\textbf{A})=I_n$ 임을 뜻한다. 1._ 기약행 사다리꼴의 선형 변환_ 행렬 $\textbf{A}$의 기약행 사다리꼴을 구하는 것을 선형 변환으로 나타낼 수 있고, 선형 변...

1.전치 행렬 주어진 행렬의 행과 열을 반전시킨 행렬을 말한다. $$ \textbf{A}{m\times n} \quad , \quad \textbf{A}^{T}{n\times m} \quad , \quad (\textbf{A}^T)^T = \textbf{A} \\ \, \\ \textbf{B} = \begin{bmatrix}1 & 2 \\ 3 & 4\end...

1. 직교여공간 직교여공간이란 2개 벡터가 서로 수직할 때 이를 직교라고 말하고, $\perp$ 기호를 사용한다. 직교인 2개 벡터들을 내적하면 값이 0이 나오는 특징을 가지고 있다. 직교여공간은 부분공간이다. $\textbf{V}^{\perp} \;=\; \{\vec{x} \in \mathbb{R}^n \;\,|\,\; \vec{x}\cd...

log 함수에 대한 간단 정리 !

선형방정식

행렬

역행렬

행렬식

수열의 극한

미분법

적분법

수학

정규분포

최소제곱회귀

순열과 조합

확률변수

표본통계량

신뢰구간

유의성 검정 (가설 검정)