[Linear Viscoelasticity] 06. Linear Viscoelasticity Model

jmt·2024년 2월 26일
kelvin-voigt modelmaxwell modelspring-dashpot modelstandard solid model고분자선형 점탄성유변학
0

선형점탄성(Linear Viscoelasticity)

목록 보기
7/7

What is Model?

고분자 물질은 점탄성에 의해 응력(stress)가 변형(strain)과 변형률(strain rate)에 의존한다. 유변학이 생기기 이전에 고체는 후크 법칙(Hook's Law)를 따르는 선형 탄성체(linear elastic body)라고 생각했고, 액체는 뉴턴의 점성 유체 거동을 따르는 뉴턴 유체라고만 생각했다. 그렇다면 옛날 사람들 생각에 스프링(spring)으로 탄성체의 성질을 나타낼 수 있고, 대시포트(dashpot)이라는 댐퍼(damper)로 유체의 성질을 나타낼 수 있다고 생각했다. 그래서 spring과 dashpot의 조합으로 모델을 만든다면 점탄성을 표현할 수 있다고 생각하여 탄생한 것이 spring-dashpot model이다.

그렇다면 모형(model)이란 무엇인가. 실물을 모방한 것이다. 어떤 대상을 그 모양 그대로 축소시킨 것이다. 즉 어떤 제품을 만들 때, 실제로 제작하기 전에 그 제품의 어떠한 변형에 의한 stress를 계산해야할 필요가 있다. 또한 여러 점탄성 함수, 여태까지 배웠던 G(t),J(t),G′,G′′,⋯G(t), J(t), G^{\prime}, G^{\prime\prime}, \cdots, 들을 활용하여 정량화할 필요가 있다. 그러므로 앞에서 배웠던 strain(γ\gamma)과 stress(σ\sigma)의 관계를 활용하여 모델을 만들 수 있을 것이다.

Spring-Dashpot Model

앞에서 spring-dashpot model에 대한 간략한 설명을 하였다. spring-dashpot model에는 Maxwell model과 Kelvin-voigt model이 있는데 이를 설명하기 전에 spring은 탄성체(elastic body)의 성질을 나타내고, dashpot는 점성 유체(viscous fluid)의 성질을 나타낸다고 하였다. 또한 이 둘은 각각 Hook's law와 Newtonain fluid라 가정하였다. 그렇다면 다음과 같은 관계를 가지게 된다.

σs=Gsγs;σd=ηddγddt.\sigma_s = G_s \gamma_s; \quad \quad \sigma_d=\eta_d \frac{d\gamma_d}{dt}.

σs\sigma_s는 탄성체, 즉 spring에서의 응력을 계산한 것이고, σd\sigma_d는 점성 유체, 즉 dashpot에서의 응력을 계산한 것이다. spring-dashpot model은 이 2개의 요소를 조합하여 점탄성을 표현하고자 한다.

Maxwell Model

Maxwell model은 spring과 dashpot을 직렬로 연결한 model이다.

The Maxwell model is a one-dimensional model that a spring and a dashpot are connected in a series.

직렬로 연결되어 있기 때문에 받는 변형은 가산될 것이고, 응력은 각 요소의 응력과 동일할 것이다. 그럼 다음과 같이 표현할 수 있다.

γ=γs+γdσ=σs=σd\begin{aligned} \gamma &= \gamma_s + \gamma_d\\ \sigma &= \sigma_s = \sigma_d \end{aligned}

spring element == elastic element이고, dashpot element == viscous element이고, γ\gamma를 시간에 대해 미분하면, 위 식을 통해 다음과 같이 쓸 수 있다.

{γs=σG0dγddt=ση0⇒dγdt=1G0dσdt+ση0\begin{aligned} \begin{cases} \gamma_s = \frac{\sigma}{G_0} \\ \frac{d\gamma_d}{dt} = \frac{\sigma}{\eta_0} \end{cases} \Rightarrow \frac{d\gamma}{dt}=\frac{1}{G_0}\frac{d\sigma}{dt}+\frac{\sigma}{\eta_0} \end{aligned}

양변에 G0G_0를 곱해주면, (그리고 여기서 G0G_0는 Elastic Modulus에 해당할 것이다. 탄성체의 Hook's law에 의해 유도된 상수이기 때문이다.)

dσdt+σλ0=G0dγdt;λ0=η0G0\frac{d\sigma}{dt}+\frac{\sigma}{\lambda_0}=G_0\frac{d\gamma}{dt};\quad \lambda_0=\frac{\eta_0}{G_0}

여기서 λ0\lambda_0는 relaxation time이 된다. 그 이유는 λ\lambda의 단위를 파악해보면 점도, η\eta의 단위는 Pa-s이고, GG의 단위는 Pa 이기 때문에 시간의 단위를 갖게된다는 것을 알 수 있다.

위 식은 비제차 1차 선형 미분방정식이다. 적분 인자(Integrating Factor)를 통해 구하면 쉽게 해, σ(t)\sigma(t)를 구할 수 있다. 그 과정은 다음과 같다.

Solution of non-homogeneous ODE, σ(t)\sigma(t)

Integrating Factor

적분 인자 II는 다음과 같이 정의된다.

I=exp⁡(∫Pdx)wheredydx+P(x)y+Q(x)I = \exp\left(\int P dx\right)\quad where\quad \frac{dy}{dx}+P(x)y+Q(x)

이를 위에서 구한 비제차 선형 방정식의 적분인자를 구하여 양변에 곱해주면 다음과 같이 유도된다.

I=exp⁡(∫1λ0dt)=exp⁡(t/λ0)dσdtet/λ0+σλ0et/λ0=G0et/λ0dγdtddt(et/λ0σ)=G0et/λ0dγdt\begin{aligned} I = \exp\left(\int \frac{1}{\lambda_0}dt\right) &=\exp\left(t/\lambda_0\right)\\ \frac{d\sigma}{dt}e^{t/\lambda_0}+\frac{\sigma}{\lambda_0}e^{t/\lambda_0} &= G_0e^{t/\lambda_0}\frac{d\gamma}{dt}\\ \frac{d}{dt}\left(e^{t/\lambda_0}\sigma\right) &= G_0e^{t/\lambda_0}\frac{d\gamma}{dt} \end{aligned}

양변을 적분인자 τ\tau에 대해 −∞-\infin에서 tt까지 적분하면,

et/λ0σ−lim⁡t→−∞et/λ0σ=∫−∞tG0eτ/λ0dγdτdτe^{t/\lambda_0}\sigma - \lim_{t\rightarrow-\infin}e^{t/\lambda_0}\sigma =\int^t_{-\infin}G_0e^{\tau/\lambda_0}\frac{d\gamma}{d\tau}d\tau

σ(t)\sigma(t)에 대해 정리하면,

σ(t)=∫−∞tG0e−(t−τ)/λ0dγdτdτ\sigma(t)=\int^t_{-\infin}G_0e^{-(t-\tau)/\lambda_0}\frac{d\gamma}{d\tau}d\tau

G(t)G(t)

선형 응답 조건에 의해 Boltzmann superposition principle(BSP)로 정의하였던 σ(t)\sigma(t)의 정의에 의해 G(t)G(t)는 다음과 같다.

σ(t)=∫−∞tG(t)dγdτdτ\sigma(t) = \int^t_{-\infin}G(t)\frac{d\gamma}{d\tau}d\tau
G(t)=G0et/λ0Θ(t)G(t) = G_0 e^{t/\lambda_0} \Theta(t)

그럼 우리는 이제 Maxwell model로 얻은 G(t)G(t)로 dynamic moduli(G′,G′′)G^{\prime}, G^{\prime\prime})과 라플라스 변환에 의하면 sG~(s)=1/sJ~(s)s\tilde G(s) = 1/s\tilde J(s) 이므로 , creep compliance J(t)J(t)도 구할 수 있다. 구하는 과정은 어렵지 않기에 생략하겠다. 시리즈의 이전 글을 복습하면서 잘 구해보자.

Voigt Model

Voigt model 혹은 Kelvin-Voigt model이라 부르는 이 모델은 spring과 dashpot element를 병렬로 연결한 것이다. 그렇기에 해당 모델에서 받게되는 strain은 spring, dashpot의 strain과 같다. 하지만 받게되는 응력은 가산된다.

σ=σs+σd;γ=γs=γd\sigma = \sigma_s + \sigma_d;\quad\quad \gamma=\gamma_s=\gamma_d

그러므로

σ=G0γ+η0dγdt\sigma=G_0\gamma + \eta_0 \frac{d\gamma}{dt}

Integrating Factor

위 식에서 양변을 η0\eta_0로 나누면,

dγdt+G0η0γ=1η0σ\frac{d\gamma}{dt}+\frac{G_0}{\eta_0}\gamma = \frac{1}{\eta_0}\sigma

η0/G0\eta_0/G_0를 τ0\tau_0라 하자. 그럼 적분 인자 II는 다음과 같다.

I=exp⁡(∫η0dt)]=et/η0\begin{aligned} I &= \exp\left(\int\eta_0dt\right)]\\ &= e^{t/\eta_0} \end{aligned}

J(t)J(t)

G(t)G(t)를 구했을 때와 동일하게 유도한다. 먼저 양변에 적분 인자 II를 곱하면,

ddt(et/τ0)γ=G0et/τ0σ\frac{d}{dt}\left(e^{t/\tau_0}\right)\gamma=G_0e^{t/\tau_0}\sigma

양변을 −∞-\infin에서 tt까지 적분하면,

et/τ0γ(t)−lim⁡t→−∞et/τ0γ(t)=1η0∫−∞tet/τ0σ(τ)dτe^{t/\tau_0}\gamma(t)-\lim_{t\rightarrow-\infin}e^{t/\tau_0}\gamma(t) = \frac{1}{\eta_0}\int^t_{-\infin}e^{t/\tau_0}\sigma(\tau)d\tau

우변의 적분식을 부분 적분을 이용하여 나타내면,

∫−∞tet/τ0σ(τ)dτ=τ0[et/τ0σ(τ)]τ=−∞τ=t−∫−∞tτ0et/τ0dσdτdτ=τ0et/τσ(t)−∫−∞tτ0et/τ0dσdτdτ=τ0[et/τ0∫−∞tdσdτdτ−∫−∞teτ/τ0dσdτdτ]\begin{aligned} \int^t_{-\infin}e^{t/\tau_0}\sigma(\tau)d\tau &= \tau_0\left[e^{t/\tau_0}\sigma(\tau)\right]^{\tau=t}_{\tau=-\infin} - \int^t_{-\infin}\tau_0e^{t/\tau_0}\frac{d\sigma}{d\tau}d\tau\\ &= \tau_0e^{t/\tau}\sigma(t) - \int^t_{-\infin}\tau_0e^{t/\tau_0}\frac{d\sigma}{d\tau}d\tau\\ &= \tau_0\left[e^{t/\tau_0}\int^t_{-\infin}\frac{d\sigma}{d\tau}d\tau-\int^{t}_{-\infin}e^{\tau/\tau_0}\frac{d\sigma}{d\tau}d\tau\right] \end{aligned}

위 식을 우변에 대입하고 양변을 et/τ0e^{t/\tau_0}로 나누면, BSP에 의한 γ(t)\gamma(t)의 정의에 의해 J(t)는 다음과 같다.

γ(t)=e−t/τ0G0∫−∞t(et/τ0−eτ/τ0)dσdτdτ=J0∫−∞t[1−e−(t−τ)/τ0]dσdτdτJ(t)=J0(1−e−t/τ0)Θ(t)\begin{aligned} \gamma(t) &= \frac{e^{-t/\tau_0}}{G_0} \int^t_{-\infin} \left(e^{t/\tau_0}-e^{\tau/\tau_0} \right) \frac{d\sigma}{d\tau} d\tau \\ &= J_0 \int^t_{-\infin}\left[1-e^{-(t-\tau)/\tau_0} \right]\frac{d\sigma}{d\tau}d\tau\\ J(t) &= J_0 \left(1-e^{-t/\tau_0}\right)\Theta(t) \end{aligned}

Standard Solid Model

Maxwell model은 relaxation modulus는 잘 정량화할 수 있지만, creep compliance를 잘 나타내주지는 못한다. Voigt model은 그 반대이다. 그래서 standard solid model을 사용하는데, 이는 Maxwell model과 Voigt model의 가장 간단한 조합이다.

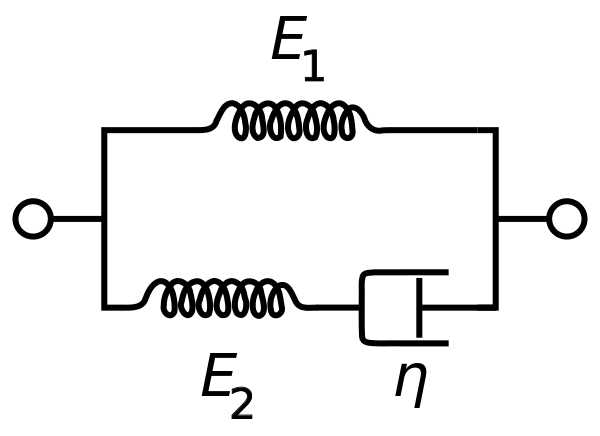
EE를 GG라고 생각하자.

Maxwell model

먼저 Maxwell model의 경우에 다음을 따른다.

{σ=ση=σG2γ=γη+γG2\begin{cases} \sigma = \sigma_{\eta} = \sigma_{G_2}\\ \gamma = \gamma_{\eta} + \gamma_{G_2} \end{cases}

ση와σG2\sigma_{\eta}와 \sigma_{G_2}는 각각 dashpot element와 spring element의 응력이므로 다음과 같다.

σG2=G2γG2⇒γG2=σG2G2=σG2ση=η0dγηdt⇒dγηdt=σηη0=ση0\begin{aligned} \sigma_{G_2} &= G_2 \gamma_{G_2} \Rightarrow \gamma_{G_2} = \frac{\sigma_{G_2}}{G_2} = \frac{\sigma}{G_2}\\ \sigma_{\eta} &= \eta_0 \frac{d\gamma_{\eta}}{dt} \Rightarrow \frac{d\gamma_{\eta}}{dt} = \frac{\sigma_{\eta}}{\eta_0} = \frac{\sigma}{\eta_0} \end{aligned}

그리고 γ\gamma에 대한 식을 미분하면,

dγdt=dγηdt+dγG2dt=ση0+1G2dσdtG2dγdt=σλ2+dσdt.\begin{aligned} \frac{d\gamma}{dt} &= \frac{d\gamma_{\eta}}{dt} + \frac{d\gamma_{G_2}}{dt}\\ &= \frac{\sigma}{\eta_0} + \frac{1}{G_2}\frac{d\sigma}{dt}\\ G_2\frac{d\gamma}{dt} &= \frac{\sigma}{\lambda_2} + \frac{d\sigma}{dt}. \end{aligned}

위에서 구한 σ,γ\sigma, \gamma는 모두 Maxwell model에서의 stress와 strain임을 유의하자.

Vogit model

이제 maxwell model과 spring element가 병렬 연결되어 있는 Voigt model을 고려하면,

{σ=σG1+σmaxwellγ=γG1=γmaxwell\begin{cases} \sigma = \sigma_{G_1} + \sigma_{maxwell}\\ \gamma = \gamma_{G_1} = \gamma_{maxwell} \end{cases}

그리고 σG1\sigma_{G_1}는 spring element이므로 후크의 법칙을 따른다는 것을 안다.

σG1=G1γ\sigma_{G_1} = G_1 \gamma

이제 σ\sigma에 대한 식을 시간에 대해 미분하면 다음과 같다.

dσdt=G1dγdt+dσmaxwelldt=G1dγdt+G2dγdt−σλ2=(G1+G2)dγdt−σ−σ1λ2\begin{aligned} \frac{d\sigma}{dt} &= G_1\frac{d\gamma}{dt}+\frac{d\sigma_{maxwell}}{dt}\\ &= G_1\frac{d\gamma}{dt} + G2\frac{d\gamma}{dt}-\frac{\sigma}{\lambda_2}\\ &= \left(G_1+G_2\right)\frac{d\gamma}{dt}-\frac{\sigma-\sigma_1}{\lambda_2}\\ \end{aligned}

그러므로

dσdt+σλ2=(G1+G2)dγdt+G1λ2γ\frac{d\sigma}{dt}+\frac{\sigma}{\lambda_2}=\left(G_1 + G_2\right)\frac{d\gamma}{dt} + \frac{G_1}{\lambda_2}\gamma

이고, γ(t)=γ0Θ(t)\gamma(t)=\gamma_0\Theta(t)라 하고 라플라스 변환을 사용하여 relaxation modulus를 구하면 다음과 같다.

G(t)=(G1+G2−t/λ2)Θ(t)G(t) = \left(G_1 + G_2^{-t/\lambda_2}\right)\Theta(t)

Multi-Mode Models

profile
jmt
고분자/컴공
이전 포스트

[Linear Viscoelasticity] 05. Rheometers

0개의 댓글

관련 채용 정보