Introduction

이때까지 flow network의 maximum flow를 구하는 방법과 핵심 아이디어가 되는 포드-풀커슨 방법과 이를 구현한 알고리즘인 에드몬드-카프 알고리즘을 배웠다. 이번에는 이를 이용해 이분 그래프(bipartite graph)가 무엇인지 배워보고 maximum bipartite matching은 어떻게 할 수 있는지 배워보자.

Bipartite Graph

이분 그래프는 모든 인접한 vertex끼리 서로 다른 색으로 칠했을 때, 모든 vertex가 두 가지 색으로만 칠해지는 그래프를 의미한다. 즉, 그래프의 모든 vertex가 $V, U$라는 2개의 disjoint set으로 나누어져 있게 되고, 모든 edge는 $V$와 $U$를 이어야 한다.

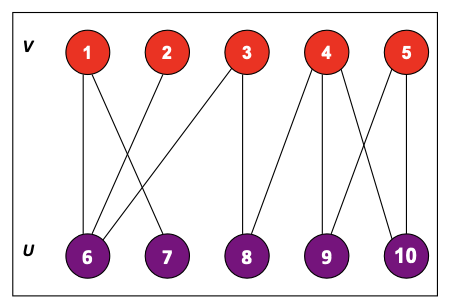
Matching in a Graph

주어진 무방향 그래프 $G = (V, E)$에 대해 하나의 매칭(matching)은 간선의 부분집합($M \subseteq E$)을 의미한다. 이때 모든 정점 $v \in V$에 대해 $M$에서 최대 한 개의 edge는 $v$를 잇는다. 그리고 어떤 vertex $v \in V$가 매칭 $M$의 한 edge에 의해 이어지면, $v$는 '매칭된다'라고 한다. 그렇지 않다면 $v$는 '매칭이 안 된다' 라고 한다. 최대 매칭이라는 것은 결국 최대 크기를 가진 매칭을 의미한다. 다시 말해, 최대 매칭 $M$은 임의의 매칭 $M^{\prime}$에 대해 $|M| \ge |M^{\prime}|$을 만족해야 한다.

Maximum Bipartite Matching Problem

최대 이분 매칭 문제는 결국 이분 그래프에서 최대 매칭 $M$을 찾는 문제이다. 주어진 이분 그래프 $G = (V, E)$에서 polynomial time 내에 최대 매칭을 찾기 위해서는 포드-풀커슨 방법을 사용할 수 있다. 그 방법은 아래 그림과 같다.

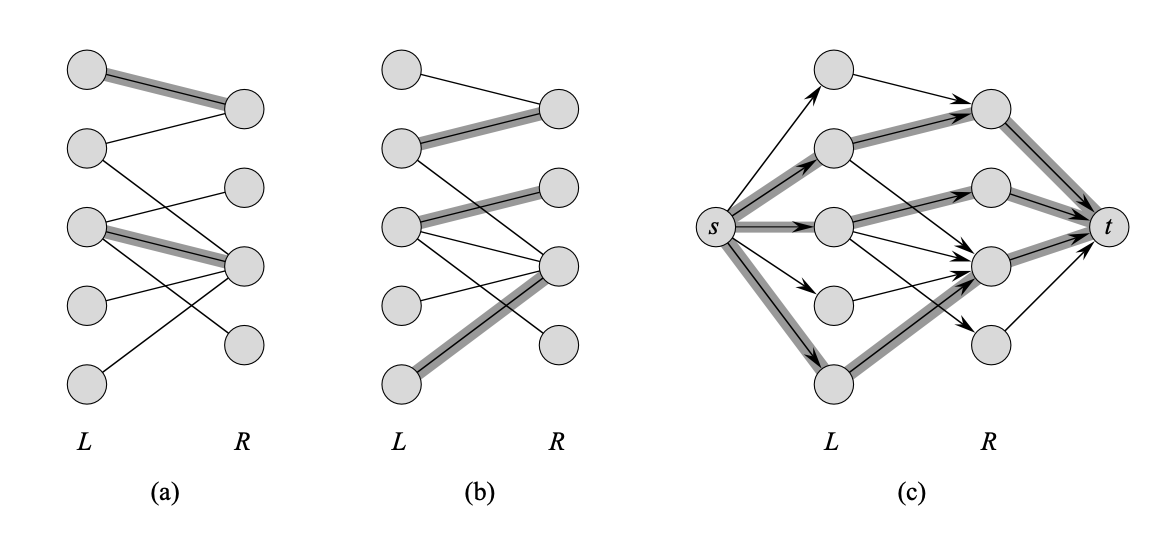
그래프 $G$의 vertex들의 집합 $V$를 $L, R$로 나눌 수 있으면 이분 그래프이다. 그리고 위 그림의 (c)와 같이 source $s$ vertex와 sink $t$ vertex를 추가하여 하나의 flow network를 만들면 된다. 그 뒤 우리가 기존에 하던 포드-풀커슨 방법을 적용시키면 풀 수 있다. 예를 들어 가장 위에 있는 이분 그래프를 예시로 적용해보자. $V$에 속하는 vertex들은 모두 source $s$ vertex와 연결되어 있고, $U$에 속하는 vertex들은 모두 sink $t$ vertex와 연결되어 있다고 하자. 또한 $s$와 $t$를 새로 추가했고, $s, t$와 기존의 vertex들이 연결되어 있는 새로운 flow network를 나타내는 그래프를 $G^{\prime} = (V^{\prime}, E^{\prime})$이라 하자.

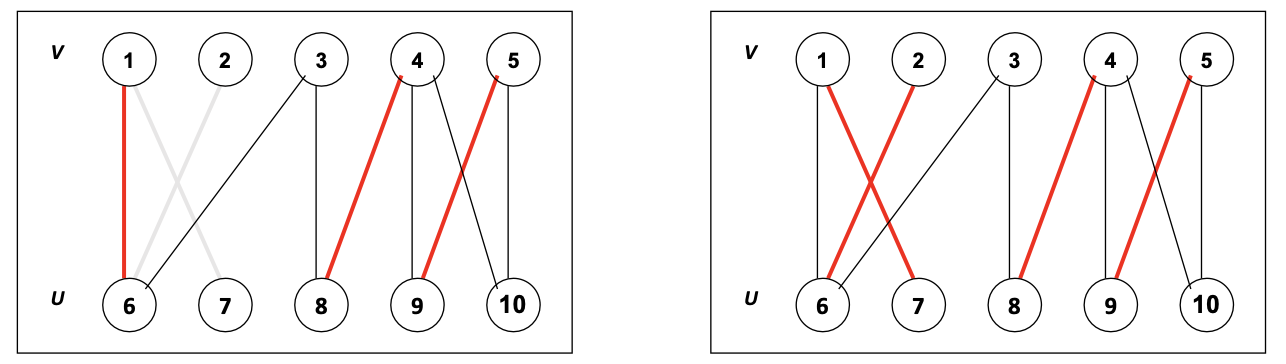
왼쪽과 같이 빨간색으로 칠해진 edge가 현재 Matching이라고 하자. 왼쪽 그림에서 residual network를 만들고, residual network에 존재하는 증강 경로, $s$에서 $t$로 도착하는 path가 있는지 찾아본다. 그 결과 $s \rightarrow 2 \rightarrow 6 \rightarrow 1 \rightarrow 7 \rightarrow t$의 path를 발견할 수 있었다. 그리고 포드-풀커슨 방법에 따라 augmentation을 수행하게 되면, 새로운 flow가 있는 flow network는 위 그림의 오른쪽이 된다. 그리고 다시 residual network를 그려 증강 경로가 있는 지 찾아보면, 존재하게 된다. 해당 경로는 $s \rightarrow 3 \rightarrow 8 \rightarrow 4 \rightarrow 9 \rightarrow 5 \rightarrow 10 \rightarrow t$가 된다. 다시 augmentation을 수행하면, 아래의 그림과 같은 새로운 flow network가 그려진다.

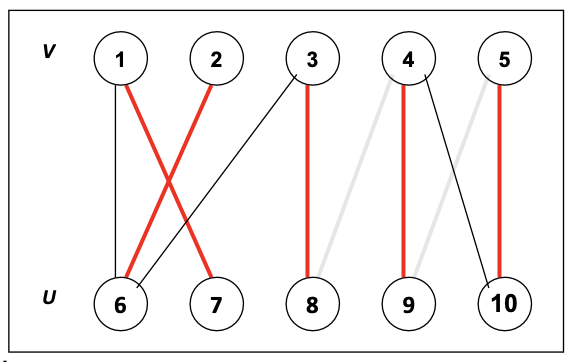
그리고 해당 flow network의 residual network에는 더 이상의 증강 경로가 존재하지 않는다. 그렇기에 현재 flow network의 최대 유량이 흐르고 있다는 것을 알 수 있고, 이것이 곧 Maximum Matching. 최대 이분 매칭 문제를 해결하게 된 것이다. $|M| = 5$가 된다.

Analysis

기존 이분 그래프의 모든 vertex는 최소한 하나의 edge를 가지게 된다. 그렇기에 다음을 따른다.

또한 이분 그래프에서 flow network를 형성하면서 $s$와 $t$가 각각 기존의 vertex들과 이어지는 새로운 edge를 추가했다. 이는 $|E^{\prime}| = |E| + |V|$를 의미한다. 그렇기에 다음과 같이 정리할 수 있다.

최종적으로 $|E^{\prime}| = \Theta(E)$가 된다.

이분 그래프에서 모든 매칭은 크기가 최대 $\text{min}(L, R)$이므로 $O(V)$가 된다. 그렇기에 $G^{\prime}$의 최대 유량의 값도 $O(V)$가 된다. 결론적으로 이분 그래프에서 maximum matching을 찾는데 걸리는 시간은 $O(VE^{\prime})=O(VE)$이라 할 수 있다.