Introduction
Ford-Fulkerson Method(포드-풀커슨 방법)은 3가지 중요 아이디어에 의존한다. 앞에서 배운 잔여 네트워크(residual network) / 증강 경로(augmenting path) / cut이다. 이 3가지 개념은 Max-flow Min-cut 정리에 활용된다.
포드-풀커슨 방법은 flow 값을 반복적으로 증가시킨다. 모든 u,v∈V에 대해 f(u,v)=0으로 초기화시킨 뒤, 매 단계마다 잔여 네트워크의 증강 경로를 찾는다. 증강 경로를 찾았다면, 해당 경로 p를 따라 augmentation 연산을 수행하여 flow를 증가시킨다. 만약 잔여 네트워크의 증강 경로가 더 이상 존재하지 않는다면 f를 return한다. 이 방법은 우리가 part 1에서 했던 방법과 크게 다르지 않다. 더 이상 증강 경로가 존재하지 않는 것이 maximum flow를 찾았다는 의미가 되는 것은 max-flow min-cut 정리로 증명이 가능하다.
Cut
cut에 대한 개념을 더 자세히 배워보자. flow network의 cut(S,T)은 V를 s∈S,t∈T가 되게 하는 분할이다. flow f에 대해 cut(S,T)의 net flow는 다음과 같다.
f(S,T)=u∈S∑v∈T∑f(u,v)−u∈S∑v∈T∑f(v,u)
그리고 cut(S,T)의 용량(capacity)는 다음과 같다.
c(S,T)=u∈S∑v∈T∑c(u,v)
flow network의 minimum cut은 네트워크의 모든 cut 중 용량이 최소가 되는 cut을 의미한다.
정리 1
cut에 대한 정의를 바탕으로 다음과 같은 정리를 증명해보자.
For any cut(S,T), f(S,T)=∣f∣.
이전 시간에 flow network의 flow는 flow conservation을 지켜야 했다. 그렇기에 u∈V−s,t에 대해 다음과 같이 flow conservation을 다시 쓸 수 있다.
v∈V∑f(u,v)=v∈V∑f(v,u)
∣f∣의 정의는 다음과 같았다.
∣f∣=v∈V∑f(s,v)−v∈V∑f(v,s)
flow conservation 식을 이용하면 다음과 같이 쓸 수 있다.
∣f∣=v∈V∑f(s,v)−v∈V∑f(v,s)=v∈V∑f(s,v)−v∈V∑f(v,s)+u∈S−{s}∑(v∈V∑f(u,v)−v∈V∑f(v,u))=v∈V∑f(s,v)+u∈S−{s}∑v∈V∑f(u,v)−v∈V∑f(v,s)+u∈S−{s}∑v∈V∑f(v,u)=v∈V∑⎝⎜⎛f(s,v)−u∈S−{s}∑f(u,v)⎠⎟⎞−v∈V∑⎝⎜⎛f(v,s)−u∈S−{s}∑f(v,u)⎠⎟⎞=v∈V∑u∈S∑f(u,v)−v∈V∑u∈S∑f(v,u)
여기서 V 는 S∪T이고 S∩T=∅이므로,
∣f∣=u∈S∑v∈T∑f(u,v)−u∈S∑v∈T∑f(v,u)=f(S,T) : net flow
정리 2
The value of any flow ≤ capacity of any cut.
앞의 정리 1에 의해 cut(S,V)에 대해 다음이 성립한다.
∣f∣=f(S,T)
net flow의 정의에 의해 다음이 성립한다.
f(S,T)=u∈S∑v∈T∑f(u,v)−u∈S∑v∈T∑f(v,u)≤u∈S∑v∈T∑f(u,v)≤u∈S∑v∈T∑c(u,v)=c(S,T)
그러므로 어떤 flow network의 maximum flow는 항상 flow network의 minimum cut의 용량보다 작거나 같다. 이를 통해 Max-flow Min-Cut 정리를 유도할 수 있다.
Max-Flow Min-Cut Theorem
다음은 동치이다.
1. G의 절단 cut(S,T)에 대해 ∣f∣=c(S,T)이다.
2. f 는 G의 최대 유량(maximum flow)이다.
3. 잔여 네트워크(residual network) Gf는 증강 경로를 가질 수 없다.
1.→2. 그리고 2.→3 마지막으로 3→1의 순서로 증명해보자. 우선 모든 cut에 대해 ∣f∣≤c(S,T)가 성립한다. 여기서 ∣f∣=c(S,T)가 되면 f는 더 이상 증가하지 않을 것이다. 그러므로 f가 최대 유량이 된다. 그리고 2→3을 귀류법으로 증명해보자. f가 최대 유량이 아니라면, Gf의 증강 경로에 의해 ∣f∣가 증가할 수 있게 된다. 정리 2에서 ∣f∣의 상한선은 c(S,T)이므로 모순이 된다. 마지막으로 3.→1.를 증명해보자.
우선 Gf에 증강 경로가 없다고 가정하고 다음 그림과 같은 cut을 생각해보자.
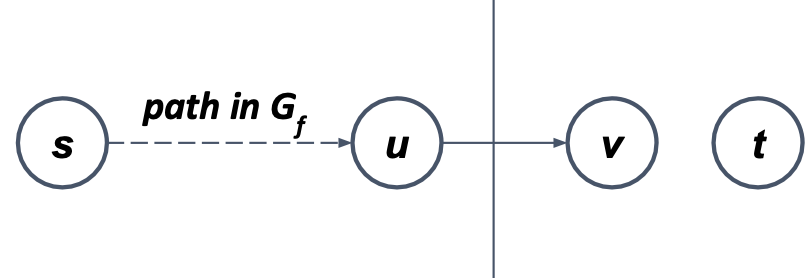
ST={v∈V, there exists a path in Gf from s to v}=V−S
위와 같은 cut에서 (u,v)∈E이면, f(u,v)=c(u,v)가 된다. 그렇지 않다면, (u,v)∈Ef가 되므로 v가 집합 S에 속해야 한다. 그리고 (v,u)∈E이면, f(v,u)=0이 되어야 한다. 그렇지 않다면, c(v,u)가 양수가 되고 이는 (v,u)∈Ef이므로 v가 집합 S에 속하는 모순이 발생한다. 결론적으로 다음이 성립한다는 의미이다.
f(S,T)=u∈S∑v∈T∑f(u,v)−u∈S∑v∈T∑f(v,u)=u∈S∑v∈T∑c(u,v)−u∈S∑v∈T∑0=c(S,T)
Basic Ford-Fulkerson Method

Introduction에서 설명한 포드-풀커슨 방법에 앞에서 언급한 정리들을 활용하여 수도 코드로 작성한 결과이다. 이를 적용하여 다음의 예제를 살펴보자.
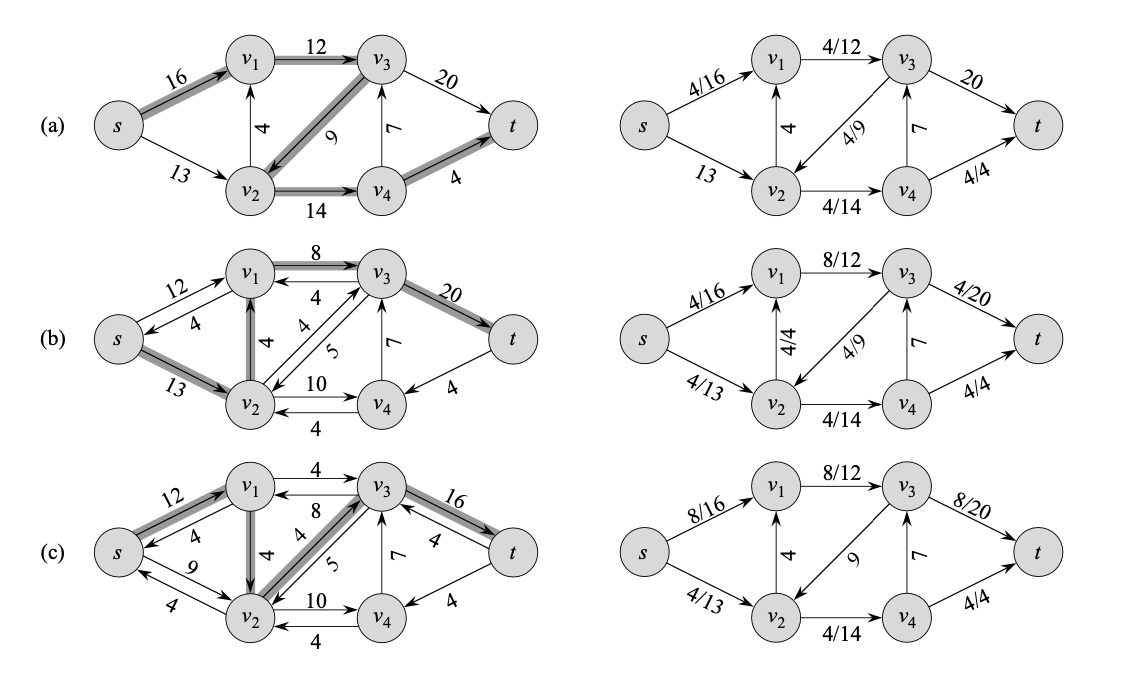
(a)를 보면, 주어진 flow network에 초기에 f=0으로 초기화한다. 그 후 (b)와 같이 residual network를 만들 수 있고, 잔여 네트워크의 증강 경로 p를 찾아 cf(p)를 구하면 4가 된다. 그 후 line 5~8의 반복문을 따라가며 해당 증강 경로 p에 속하는 edge(u,v)가 flow network G의 E에 속한다면 cf(p)만큼 더하고 속하지 않는다면 cf(p)를 빼준다. 그 결과가 (b)의 오른쪽 그래프와 같다. 이에 대한 잔여 네트워크를 다시 구하면 (c)와 같고, 증강 경로 p가 존재하는 것을 확인할 수 있다. 이 증강 경로의 cf(p)를 구하면 또 4이고, 다시 line 5~8의 반복문을 따라가면 (c)의 오른쪽 그래프를 얻을 수 있다. 이 과정을 아래 그림의 (e)까지 반복한다.
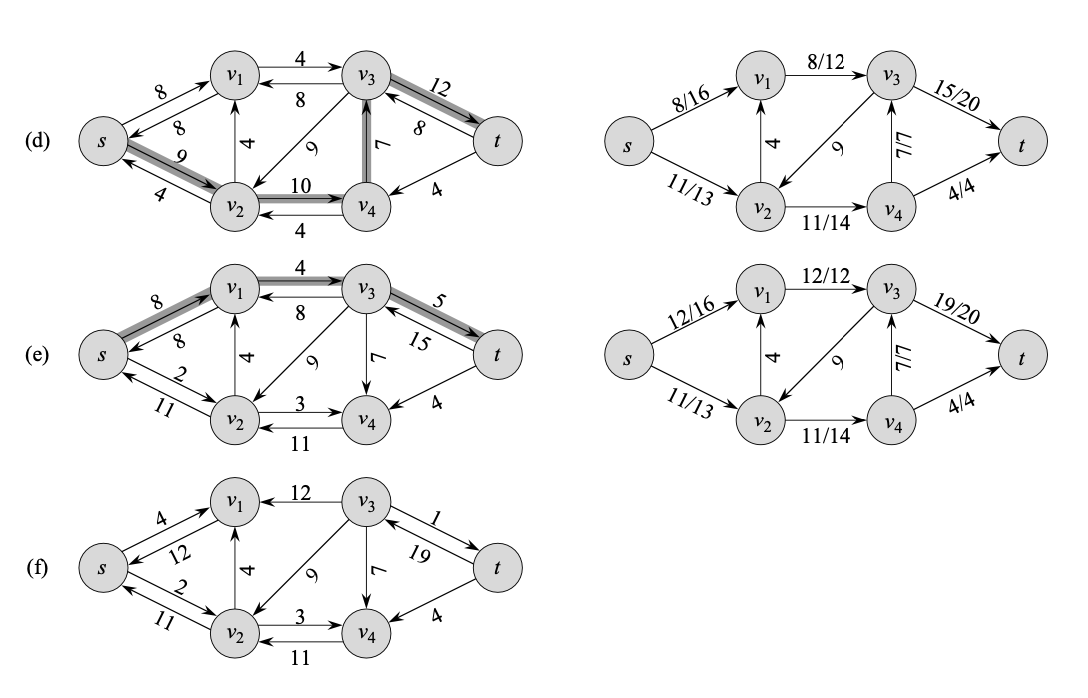
(e)의 오른쪽 flow network의 잔여 네트워크를 구하면 (f)와 같고, 더 이상 잔여 네트워크에 증강 경로가 존재하지 않기 때문에 (e)의 flow가 최대 유량(maximum flow = 23)가 된다.
Analysis of Ford-Fulkerson
포드-풀커슨 방법의 수행시간은 line 3의 증강 경로 p를 찾는 방법에 의해 결정된다. 증강 경로를 잘못 선택하면 알고리즘이 종료되지 않거나 최대 유량으로 수렴하지 않을 수도 있는데, 이는 너비 우선 탐색(BFS) 방법을 이용하여 증강 경로를 찾아 해결할 수 있다. BFS를 사용하면 잔여 네트워크에 존재하는 증강 경로 p를 찾는데 걸리는 시간은 O(V+E′)=O(E)이다. 여기까지는 line 3이후의 while문을 수행하는데 걸리는 시간이고 line 1~2에 의해 f값을 초기화하는데 걸리는 시간은 ∣f∗∣가 된다. 여기서 f∗는 변환된 flow network에서 최대 flow를 의미한다. 그러므로 포드-풀커슨 방법의 전체 수행시간은 O(E∣f∗∣)이다.
그럼 만약 ∣f∗∣가 상당히 큰 값을 가지는 경우 포드-풀커슨 방법은 얼마나 오래 걸릴까?
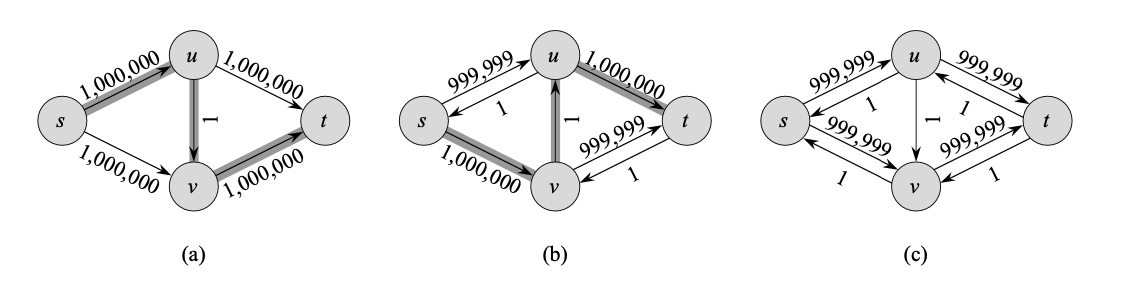
(a)의 ∣f∗∣는 2,000,000이다. (a)에 대해 포드-풀커슨 방법을 적용하면, flow는 1증가한다. flow를 1 증가시킨 flow network의 잔여 네트워크는 (b)와 같다. (b)에서 증강 경로를 그림과 같이 찾을 수 있고, 해당 경로의 cf(p)=1이 되므로, flow를 1 증가시킨다. 그럼 flow는 2가되고, 해당 flow network의 잔여 네트워크를 다시 그리면 (c)와 같다. 이 과정을 계속해서 반복해나가면 최종적으로 2,000,000에 도달할 때까지 flow를 1씩 증가시키게 된다.
Edmonds-Karp Algorithm
포드-풀커슨 방법은 알고리즘이 아니라 '방법'이다. 그 이유는 포드-풀커슨 방법을 이용하여 시간 복잡도를 개선한 여러 알고리즘이 있기 때문이다. 그 중 에드몬드-카프 알고리즘은 증강 경로 p를 찾는데 BFS를 활용하여 최단 경로를 찾는다. 우선 다음과 같은 정리를 보자.
For all v∈V−{s,t}, δf(s,v) increases monotonically with each flow augmentation.
에드몬드-카프 알고리즘을 G에 적용될 때, source와 sink인 s,t를 제외한 모든 vertex의 대한 flow가 증가함에 따라 δf, 즉 shortest-path distance 값도 증가한다는 의미이다. 왜 그런지 알아보자.
위 정리와 반대로 vertex v∈V−{s,t}에 대해 s에서 v로의 shortest-path distance를 감소시키는 flow augmentation이 존재한다고 가정하자. f가 기존의 flow, 증강 후가 f′이라 하자. 즉,
δf′(s,v)<δf(s,v)
이 성립한다. 증강 후, 잔여 네트워크에서 찾은 s에서 v로 가는 최단 경로 p=s⇝u→v에 대해 다음이 성립한다.
δf′(s,v)=δf′(s,u)+1
v를 선택하는 방법 때문에 s에서 u까지의 거리가 감소하지는 않을 것이다. 그렇기에 다음이 성립한다.
δf′(s,u)≥δf(s,u)
여기서 만약 (u,v)∈Ef라면,
δf(s,v)≤δf(s,u)+1 : by tranignle inequality.≤δf′(s,u)+1=δf′(s,v)
이는 우리의 최초 전제에 모순이다. 그러므로 (u,v)∈/Ef가 된다. 그렇다면 (u,v)∈Ef′이라는 소리인데,
δf(s,v)=δf(s,u)−1
이다. 위 식에 앞서 이야기한 부등식과 식을 적용시키면,
δf(s,u)−1≤δf′(s,u)−1=δf′(s,v)−2
가 되는데 이 결론도 최초 전제에 모순이다. 즉 s에서 v로의 최단 경로 거리를 감소시키는 augmenting flow는 존재하지 않는다는 소리이다. 이를 통해 다음 정리를 성립시킬 수 있다.
에드몬드-카프 알고리즘이 flow network G=(V,E)에 대해 수행되면, 플로 증강의 총 횟수는 O(VE)가 된다.
잔여 네트워크 Gf의 edge(u,v)를 (u,v)가 존재하는 어떤 증강 경로 p에 대해, cf(u,v)=cf(p)라면, 해당 edge(u,v)를 critical edge라고 한다. 증강 경로를 따라 augmentation 연산을 수행하고 나면, 해당 critical edge는 다음 잔여 네트워크 Gf′에서 사라진다. 그리고 critical edge는 항상 모든 증강 경로에 존재하게 된다. 그렇다면 모든 ∣E∣개의 edge에 대해서 각 edge는 최대 ∣V∣/2번 critical edge가 될 수 있다. 잔여 그래프에서 간선을 만들 수 있는 O(E)개의 정점 쌍이 존재하기에, 에드몬드-카프 알고리즘이 모두 수행되는 동안 critical edge의 총 개수는 O(VE)가 된다. 증강 경로를 BFS로 찾기에 이때 걸리는 시간은 O(E)이므로, 에드몬드-카프 알고리즘의 총 수행시간은 O(VE2)이 된다.





