경북대 COMP0319 강의 기반의 정리
Introduction to algorithms 3판 참고

Introduction

알고리즘은 문제의 크기 $n$에 의존적이라고 배웠다. 즉, $n$의 크기에 따라 알고리즘의 연산 횟수가 달라진다. 점근적 표기법으로 worst case, best case, average case에서의 시간 복잡도 구할 수 있었다. 단순히 for문으로 반복하는 경우에는 계산하기 쉬웠지만, 재귀 호출로 문제를 해결하는 알고리즘의 경우에는 함수가 자기 자신을 호출하기 때문에 시간 복잡도를 구하기에 어렵다. 재귀적으로 문제를 해결하는 방법은 여러가지가 있는데 그 중 divide and conquer를 알아보자.

Divide and Conquer

in dive and conquer, we solve a problem recursively, applying three steps at each level of the recursion

분할 정복(divide and conquer) 방법은 재귀적으로 문제를 해결하며, 각 재귀 호출에서 3단계를 적용해서 문제를 해결한다. 첫번째 단계는 문제를 더 작은 크기의 subproblem으로 나눈다(divide). 그리고 두번째 단계는 재귀적으로 subproblem을 해결한다(conquer). 그 후 재귀적으로 푼 solution들을 합치면서 원래의 문제의 solution을 구한다(combine). 탐색 알고리즘에서 이진 탐색의 경우에는 divide-and-conquer까지 적용하여 문제를 해결하고, 정렬 알고리즘에서는 merge sort, quick sort의 경우가 divide-and-conquer 후 combine까지 진행하여 문제를 해결한다.

재귀 호출을 표현하는 방법에는 점화식이 있다. 예를 들어 merge Sort가 대표적인 divide-and-conquer 방식이라고 하였는데, merge sort의 $T(n)$은 다음과 같은 점화식을 따른다.

이 때 이 점화식을 풀어서 점근적 표기법으로 나타내는 방법을 알아보자.

Substitution Method

치환법은 가장 간단한 방법이다. 주어진 점화식을 보고 해의 형태를 예측하고 귀납법으로 이를 증명하는 방법이다. 예를 들어, 위와 같이 어떤 재귀적 호출로 문제를 해결하는 알고리즘의 시간 복잡도 $T(n)$이 점화식의 형태로 주어지는 경우를 가정하자.

Guess : $T(n) = n\log n + n$.

이제 귀납법으로 증명해보자.

Base Case

Inductive Hypothesis

$k<n$에서 우리의 추측이 참이라고 하자.

$k=n/2$에 대해서도 참이라면, 모든 자연수 $n$에 대해 $T(n)=n\log n + n$가 증명된다.

Recursion-tree Method

The recursion-tree method converts the recurrence into a tree whose nodes represent the costs incurred at various levels of the recursion. We use techniques for bounding summations to solve the recurrence.

재귀 트리 방법은 재귀를 트리로 변환하여 노드가 비용을 의미한다. 재귀를 해결하기 위해 바운딩 합산 기법을 사용한다.

재귀 트리에서는 각 노드가 하나의 subproblem의 비용(cost)를 의미한다. 그럼 level 당 cost를 모두 구한 뒤, 모든 level당 cost를 전부 더하면 재귀 호출의 총 cost를 구할 수 있다. 예를 들어

과 같은 점화식이 있다면, 노드가 $T(1)$될 때까지 재귀 트리를 확장해나가면 다음과 같을 것이다.

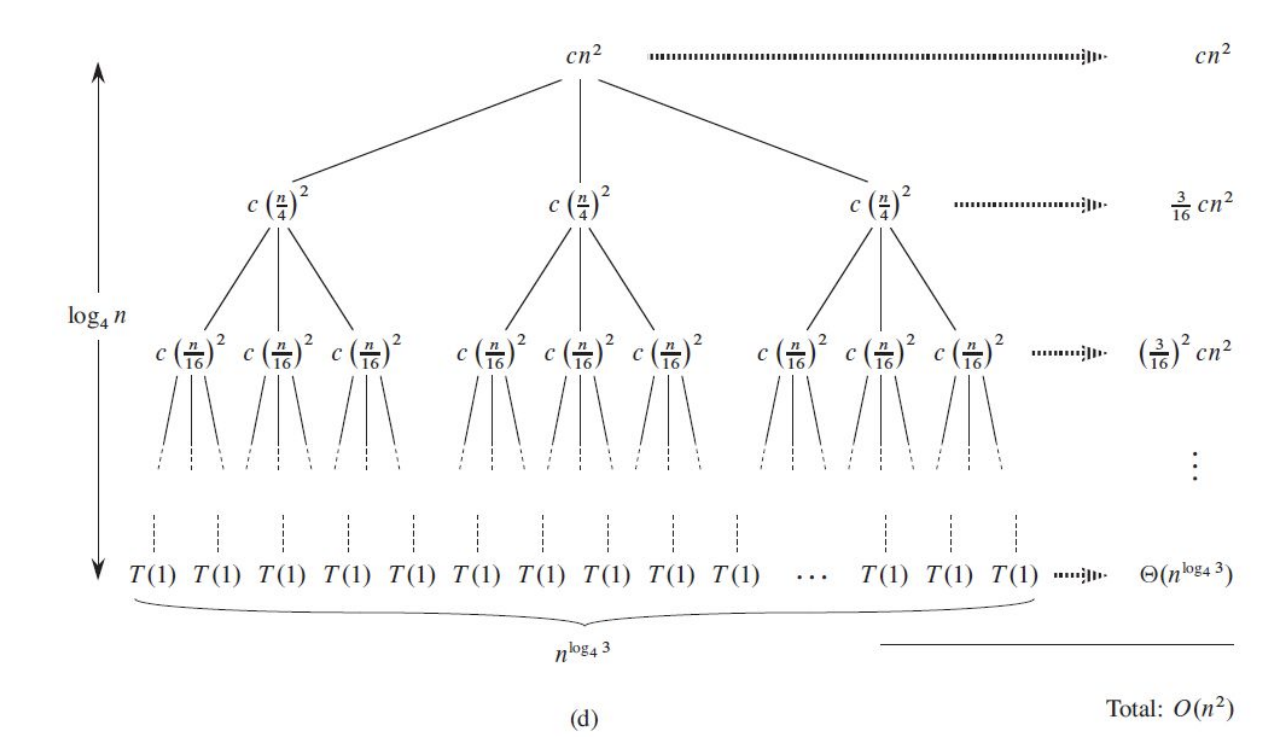
level을 $i$로 표현하고, 각 레벨 당 노드의 개수를 구해보면 규칙성에 따라 $3^i$가 된다는 것을 알 수 있다. 여기서 $i$는 0부터 시작한다. 또한 문제의 크기는 $n/4^i$가 된다는 것을 알 수 있다. 그럼 문제의 크기가 1이 될 때까지 늘어나는 level의 수는 다음과 같이 구할 수 있다.

일 때,

그럼 $T(1)$의 노드 개수는 $3^{i_{max}}$이므로

이다. 또한 각 노드의 cost는 다음과 같이 정의할 수 있다.

그러므로 $T(n)$은 다음과 같다.

Master Method

가장 먼저 배운 치환법(substitution method)는 올바른 가정을 떠올리지 못하면 의미가 없는 방법이고, 재귀 트리(recursion-tree method)는 올바른 가정을 떠올릴 수 있는 좋은 방법이지만, 너무 복잡한 경우에 재귀 트리를 그리기 힘들다. 그렇기에 마스터 정리(master method)를 사용한다. 마스터 정리의 정의는 다음과 같다.

$\text{A "Cookbook" method for solving recurrences of the form }\\T(n) = aT(n/b) + f(n)\text{ where }a\ge1\text{ and }b>1\\\text{ are constants and }f(n) \text{ is an asymptotically positive function.}$

이 때 3개의 경우로 나누어 $T(n)$의 asymptotic bound를 구한다.
$h(n) = n^{\log_b a}$이라 하면,

1. $\text{if }f(n)=O\left(\frac{h(n)}{n^{\varepsilon}}\right)\text{ for some constant }\varepsilon>0,\\\text{ then }T(n) = \Theta(h(n)).$
2. $\text{if }f(n)=\Theta(h(n)), \text{ then some constant }\varepsilon>0,\\\text{ then }T(n)=\Theta(h(n)\log n)$
3. $\text{if }f(n)=\Omega(h(n) \times n^{\varepsilon})\text{ for some constant }\varepsilon>0,\\\text{and if }af(n/b) \le cf(n) \text{ for some constant }c<1\text{ and for all sufficiently large n, then }T(n)=\Theta(f(n))$

case 1의 경우에는, 복잡한 조건을 간략화하면 $f(n) < h(n)$의 경우이다. $f(n)$의 상한선(upper bound, $O$)이 $h(n)=n^{\log_b a}$를 $n^{\varepsilon}$으로 나눈 함수로 표현 가능하다는 의미이기 때문이다. $f(n) < h(n)$이면

이 될 것이다. 그 이유는 $n$이 증가함에 따라 case 1의 경우, $h(n)$의 영향력이 더 크기 때문이다. 그러므로 $T(n) = \Theta(h(n))$이 된다.

같은 이유로 case 3의 경우에도 $f(n) > h(n)$의 경우이다. $f(n)$의 하한선(lower bound, $\Omega$)가 $h(n)$을 $n^{\varepsilon}$의 곱으로 나타냈기 때문이다. case 2의 경우에는 $f(n) = h(n)$의 경우이다.

결론적으로 재귀적인 방법으로 문제를 해결하는 알고리즘의 시간 복잡도를 점화식 $T(n) = aT(n/b) + f(n)$으로 나타낼 수 있다면, master method를 이용하여 간단히 $T(n)$의 $\Theta$-notation을 구할 수 있다.

만약 위의 경우가 복잡하다고 느낀다면 해당 시리즈의 [알고리즘 복잡도] 게시글을 참고하자.

Maximum-Subarray Problem

divide-and-conquer는 문제를 subproblems로 나누고 재귀적으로 subproblems의 solutions를 구한 뒤 합쳐서 최종적인 solution을 구하게 된다. 또한 이 때, 재귀적인 방식으로 문제를 풀다보니 총 연산 횟수, $T(n)$, 알고리즘의 시간 복잡도가 점화식으로 나타나게 되었고, $T(n)$의 상한선이 어딘지 알아보기 위해 점화식을 푸는 3가지 방법에 대해 배워보았다. 이제 divide-and-conquer 방식을 사용하여 maximum-subarray problem을 풀어보도록 하자. 이 문제에 해당하는 예시는 다음과 같다.

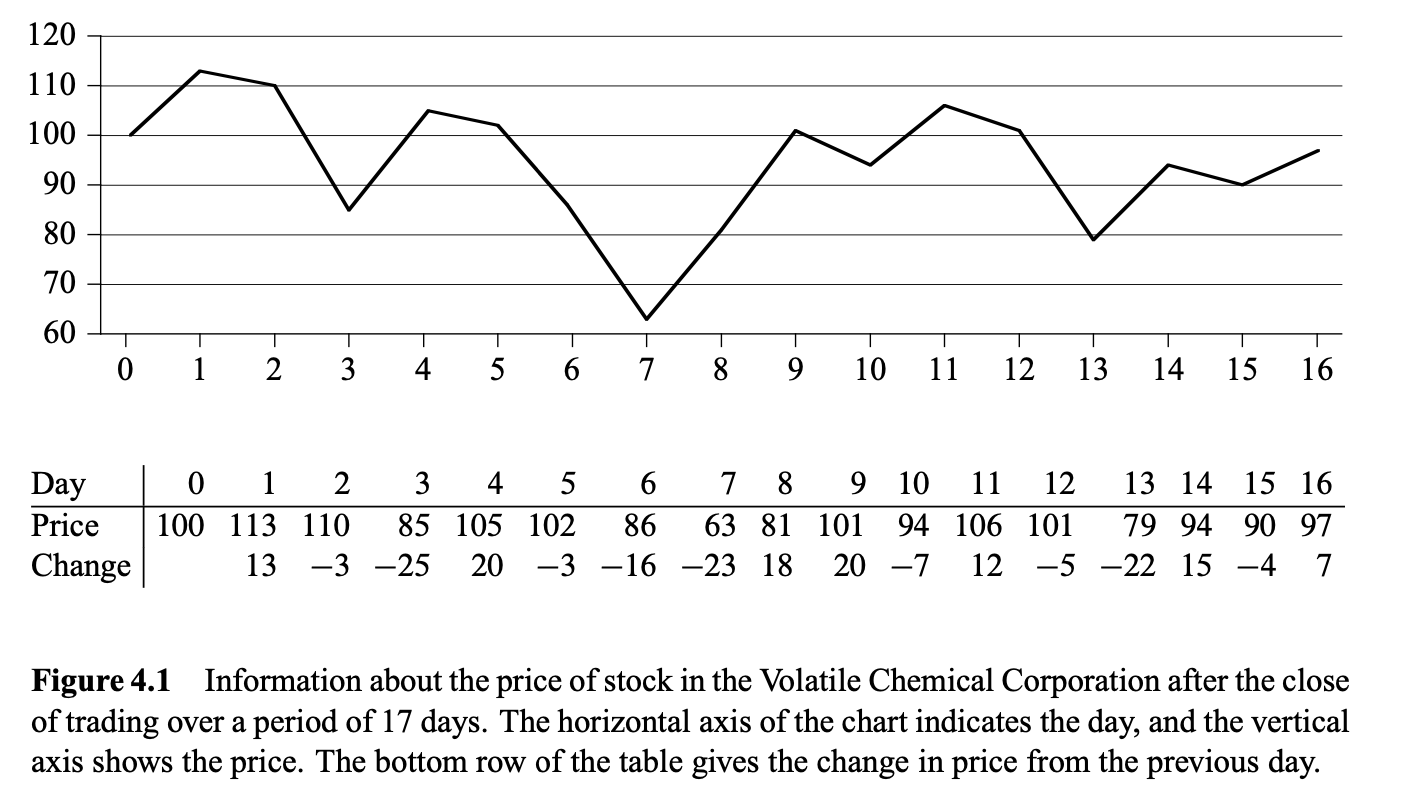
주식 투자를 할 수 있는 기회를 얻었다고 가정하자. 단 우리는 trading이 끝나고 난 뒤에 사거나 팔 수 있다. 목표는 이윤을 최대로 높이는 것이다. 즉, 가격이 가장 낮은 날 주식을 구매하고, 가장 높은 날에 팔아서 이윤을 최대로 남겨야한다.

가장 간단한 방법

이것이 왜 최대 부분배열을 구하는 문제와 동일한 문제일까? 위 그림을 보면, 우리는 간단하게 가격이 가장 낮은 날에 사고 가장 높은 날에 팔면 무조건 최대 수익을 낼 수 있을거라고 생각하지만, 아래 그림과 같은 경우가 반례로 작용하여 항상 이러한 전략이 먹힐 거라고 생각할 수 없다.

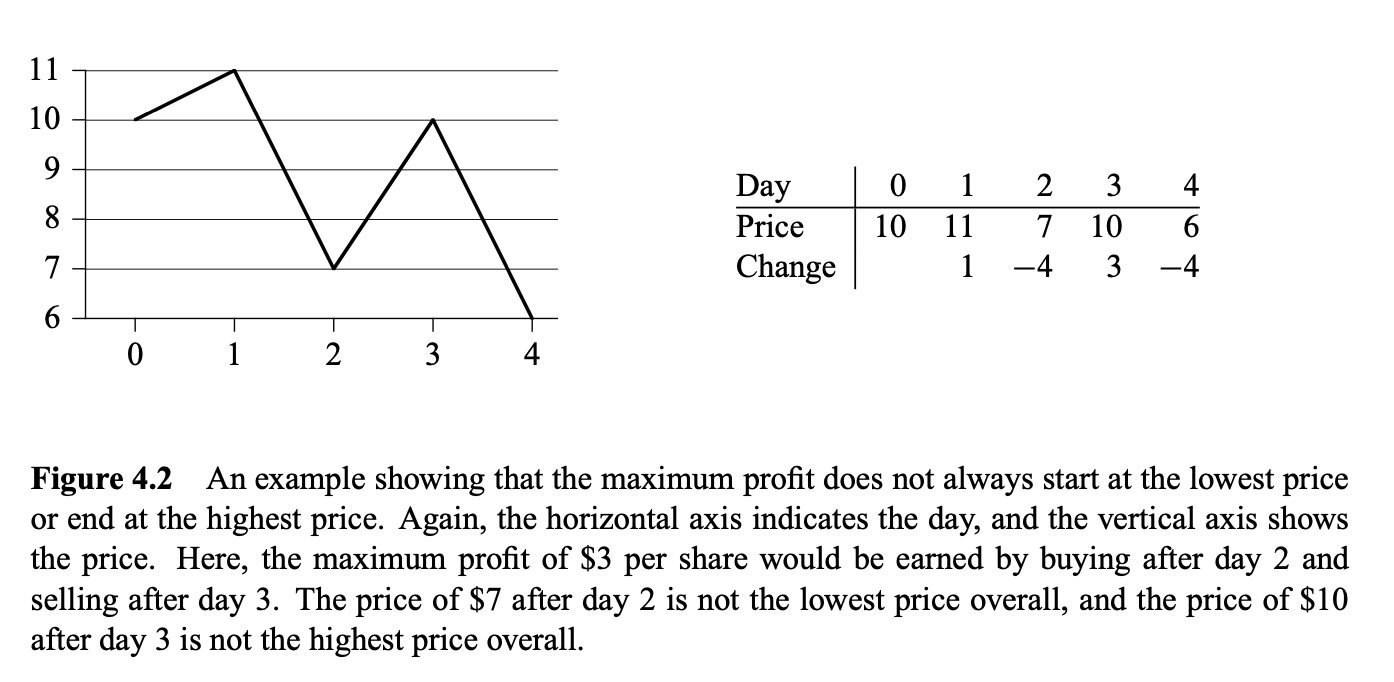
Brute-Force

그렇다면 어떻게 최대 수익을 낼 수 있을까? 완전 탐색(brute-force)방법을 가장 먼저 떠올릴 수 있다. 위 그림에서 day 0에 주식을 샀다고 가정한다면, day 1, day 2, day 3, day 4에 팔 수 있다. day 1에 샀다면, day 2, day 3, day 4에 팔 수 있다. 팔 때 수익을 계산하기 위해 Change를 판 날까지 더해가며 수익을 구한다. 간단히 코드를 작성해보면,

int max = Integer.MIN_VALUE;
for(int i=0; i<n; i++) { // n = size.
  	int sum = 0;
	for(int j=i+1; j<n; j++ {
        sum += arr[j]
    }
    if (max < sum) {
    	max = sum;	
    }
}

와 같은 형태가 된다. 문제의 크기가 $n$일 때(day가 $0 \sim (n-1)$까지 있을 때), 이중 반복문이므로, $O(n^2)$이 된다.

Divide-and-Conquer

$O(n^2)$의 시간복잡도를 가지기 때문에 $n$의 크기가 상당히 클 경우 답을 구하는데 꽤나 오래걸릴 것 같다고 추측할 수 있다. 이보다 더 효율적인 알고리즘을 찾기 위해 우리는 divide-and-conquer 기법을 떠올렸다. divide-and-conquer 기법은 우선 문제의 크기를 더 작은 subproblem으로 나누고, 재귀적으로 각 subproblems의 해를 구한 뒤, 최종적으로 합치면서 최적의 답을 구하는 방법이였다. 어떻게 위 문제에서 이를 적용할 수 있을까? 여기서 우리는 maximum-subarray의 개념을 정의하게 된다.

Maximum-subarray 이란?

그림 4.1, 4.2에서 모두 볼 수 있듯이 변화량(Change)를 나타내는 배열을 $A$라고 하자. 그럼 최대 수익을 내기 위해서 우리가 찾아야하는 것은 $A$ 하위 배열(subarray) 중에 중에 연속된 하위 배열의 합이 최대가 되는 경우를 찾아야할 것이다. 이 subarray를 maximum-subarray라고 한다.

Solution using Divide-and-Conquer

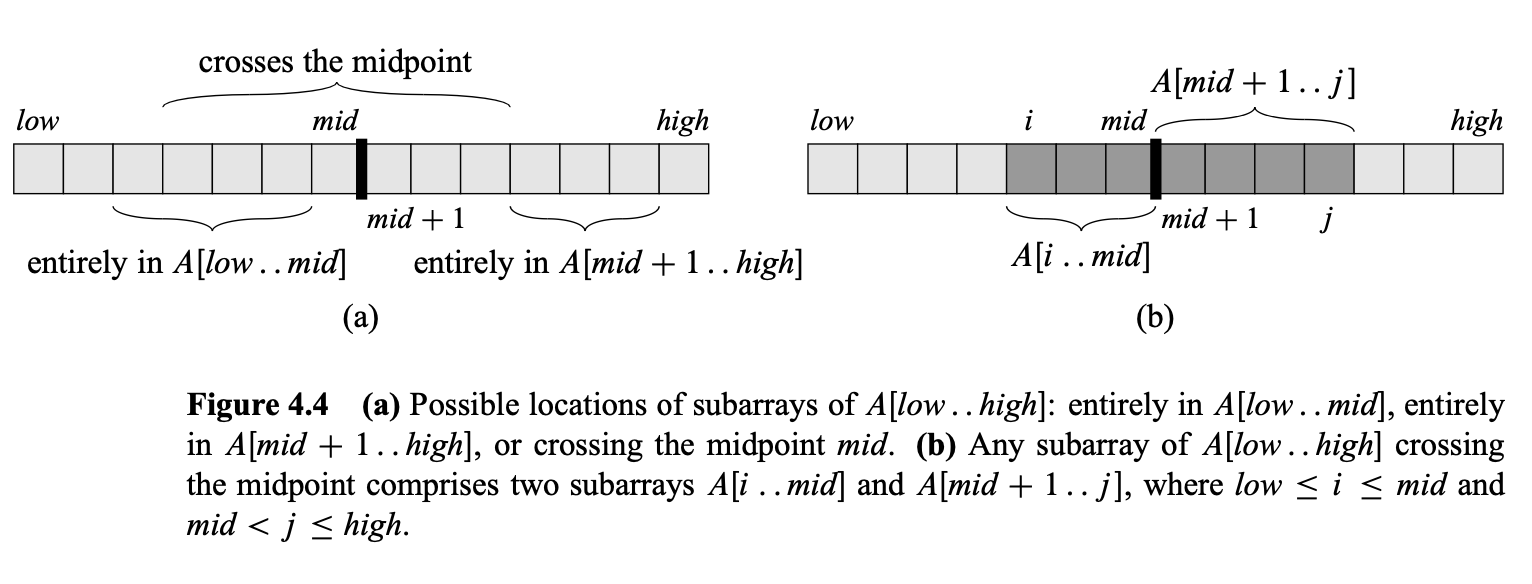
위 그림처럼 크기가 $n$인 배열 $A$를 $\frac{(low+high)}{2}$를 $mid$값을 기준으로 $n/2$의 크기인 배열 2개로 나누자(divide). 문제의 크기가 1이 될 때까지 계속해서 나눠가면서 $A[low...mid]$, $A[(mid+1)...high]$중에 연속적인 하위 배열로 이루어진 합인 "max-Left"와 "max-Right"를 구하고 그 중에 더 큰 값을 고른다면 "max-subarray"를 구할 수 있을 것이다(conquer). 다만, 여기서 위 그림을 보면 알 수 있듯이 $mid$값을 포함하는 연속적인 하위 배열의 합이 "max-subarray"가 될 수도 있다. 이를 "max-Cross"로 정의하고, "max-Left", "max-Right", "max-Cross" 중에 최대값을 고른다면 빠짐없이 "maximum-subarray"를 구할 수 있다. 물론 문제의 크기를 $n/2$로 나눌 때마다 재귀 호출하여 나눠진 배열들의 "maximum-subarray"들을 구한다면, 최종적으로 return 하는 값은 $A[1...n]$의 배열의 "maximum-subarray"를 구할 수 있게 된다(combine).

말로 설명하니 너무 복잡해지는 것 같으니 아래의 코드를 참고하자.

"max-Cross" 구하는 pseudo-code

$mid$값을 포함하는 연속적인 subarray의 합은 어떻게 구할까? 위 코드는 max-Cross를 $L=\{A|A=[l:mid] \text{ for all }l\le mid\}$과 $R=\{A|A=[mid+1:r]\text{ for all }r\ge mid\}$에서 $L$과 $R$의 max-sum인 max-left와 max-right의 합으로 구한다. max-left를 구하기 위해서는 for문이 $(mid)$ downto $(low)$까지 돌기 때문에 최대 $n/2$번, max-right를 구하기 위해서는 for문이 $(mid+1)$ to $(high)$까지 돌기 때문에 최대 $n/2$번 연산을 수행한다. 즉, max-Cross를 구하기 위해 최대 $n$번 연산을 한다.

"Maximum-Subarray" 구하는 pseudo-code

시간 복잡도

Solution using Divide-and-Conquer 에서 설명했듯이 "max-Left", "max-Right", "max-Cross"의 시간 복잡도는 각각 $T(n/2)$, $T(n/2)$, $\Theta(n)$이므로, $T(n)$은 다음과 같이 정의할 수 있다.

Master Method

master method에 의해 $f(n)=n$이고, $a=2, b=2$이다. 그럼, $f(n)=h(n)$이므로 위에서 정의한 case 2에 해당한다.

정리

brute-force 방법으로 문제를 해결하는 알고리즘은 시간 복잡도가 상당히 크기 때문에 문제의 크기가 너무 크다면, 해를 구하는데 시간이 너무 오래 걸린다. 그렇기에 우리는 더 효율적인 divide-and-conquer 방법에 대해 배웠고, 이는 재귀적으로 문제를 해결하는 방법이기 때문에 $T(n)$을 점화식으로 표현하였다. 그리고 점화식을 푸는 3가지 방법에 대해 배웠고, master method로 간단하게 시간 복잡도를 구할 수 있었다. 또한 maximum-subarray problem을 예시로 divide-and-conquer가 더 효율적임을 보였다. 다음 시간에는 divide-and-conquer와 비슷하게 복잡한 문제를 재귀적인 방법으로 간단한 하위문제로 나누어 복잡한 문제를 푸는 Dynamic Progamming 기법에 대해 배워보자. divide-and-conquer와 비슷하게 보이지만 차이점이 존재한다. 다음 시간에 자세히 다뤄보자.