[알고리즘] 05. Dynamic Programming (Part 1)

jmt·2024년 4월 9일

알고리즘

목록 보기

6/18

Introduction

dynamic programming은 divide-and-conquer와 같이 특정한 알고리즘이 아니라 기법이다. DP는 복잡한 문제를 재귀적인 문제로 간단한 subproblems로 나누어 해결하는 기법인데, 정의만 보았을 때는 divide-and-conquer와 동일해보인다. 어떤 차이가 있는지 알아보고, DP로 문제를 푸는 방법들을 알아보자.

우선 이름이 왜 dynamic programming일까? 누군가는 이유를 붙여서 설명해주기도 하지만, 직역하면 "동적 프로그래밍"이 되는데, DP에 대해 공부하다보면 전혀 "동적"과 관계가 없어보인다. 이름이 이렇게 붙여진 이유는 Richard Bellman이 미 국방부 소속인 RAND 연구소에서 DP에 대한 연구를 진행하기 위해, mathematical research를 하고 있다는 것을 피하기 위해 "Dynamic Programming"이라 이름 붙였다는 얘기가 있다. 예나 지금이나 수학을 싫어하는 사람은 많았던 것 같다.

Divide-and-Conquer VS DP

어찌됐든 DP와 divide-and-conquer의 차이점을 알아보자. 우선 둘 다 Optimal Subsructure를 띄고 있는 문제를 해결하는 방법이다. 최적 부분 구조 문제(optimal substructure problem)는 subproblems의 optimal solutions를 통해 원래 문제의 최적해를 구할 수 있는 구조를 가진 문제를 말한다. DP와 분할 정복 모두 재귀적으로 subproblems들을 해결해나가지만 큰 차이점이 존재한다.

이전 시간에 배운 divide-and-conquer의 경우에는 원래의 문제를 서로 겹치지 않는 subproblems으로 나눈다. 그리고 재귀적으로 각 subproblem의 해를 구한 뒤, 이들을 조합하여 혹은 합쳐서 원래 문제의 최적해를 구하는 방식이다. 그러나 DP의 경우에는 원래의 문제를 subproblems로 나누지만, 겹칠 수 있다. 즉, "subproblems share subsubproblems"의 구조를 띄게 된다. subproblem이 중복되다 보니 이전에 수행한 연산 결과를 재활용하여 또 다른 subproblem의 해를 구하기도 한다.

결론적으로, 분할 정복은 문제를 subproblems로 완전히 독립적으로 나누어 재귀적인 방법으로 해결하지만, DP의 경우에는 겹칠 수 있는 subproblems로 나누다 보니 앞에서 해결한 문제와 선형적으로 연결되는 특징을 가지게 된다. 이런 특징으로 인해 DP를 동적 프로그래밍으로 부르기보단 "기억하며 풀기" 혹은 "저장하며 풀기" 정도로 이해하면 더 직관적인 이해가 가능할 것이다.

이제 예시를 들어 DP로 어떻게 문제를 풀 수 있는지 알아보자.

Rod Cutting Problem

우선 DP는 최적화 문제(optimization problems)에서 주로 사용되는데, 최적화 문제라는 것은 최적의 값으로 해를 구할 수 있는 문제들을 의미한다. 예를 들면 최대값이나 최소값을 구하는 문제들이 있다. DP 기법으로 이런 최적화 문제를 풀 때, 총 4개의 단계에 따라 문제를 해결하게 되는데

최적해의 구조를 characterize
재귀적으로 최적해의 값을 구한다.
최적해의 값들을 계산해나간다. 일반적으로 "Bottom-Up" 방식으로 해결하게 된다.
계산된 정보로 최적해(optimal solution)를 구한다.

rod cutting problem이란 steel rod를 몇 개의 조각들로 나누어야 최대 이익을 남길 수 있을까?를 구하는 문제이다. 여기에 조건은

자르는 비용은 없다.
rod의 길이는 항상 정수로 주어진다.

이를 수식으로 나타내기 위해,

input : A length $n$ and table of prices $p_i$ , for $i=1, 2, \cdots, n$
Output : 얻을 수 있는 최대 이익은 조각들로 나누어진 rods의 길이에 대한 $p_i$ 의 합이 된다.

만약, $p_n$ 이 충분히 커서 최적 해가 cut를 하지 않는 경우가 되면, 길이가 $n$ 인 상태로 그대로 두어야 한다.

그대로 한 번 풀어보자. 길이가 4( $n=4$ )이고 $p_4=9$ 인 경우를 가정하자. 또한 table of prices $p_i$ 는 다음과 같다.

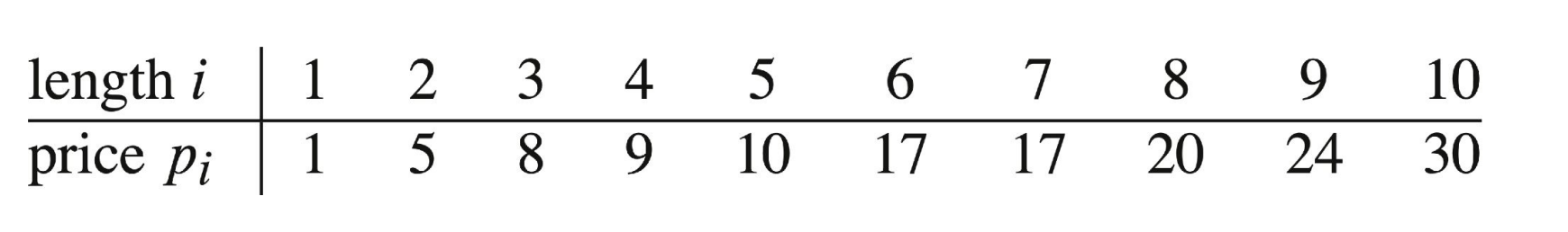
그럼 총 8개의 경우를 가질 수 있다. 자를 수 있는 구간이 총 3개이기 때문에 경우의 수를 구하면 $2^3 = 8$ 이기 때문이다. 이제 어디를 잘라야 최대 이윤을 남길 수 있을지 어떻게 구할까? DP 기법은 bottom-up 방식으로 subproblems들을 재귀적으로 해결해나가며(subproblem의 optimal solution을 구하며), 이전의 연산 결과를 이용하여 원래 문제의 최적해를 구한다고 하였다. 혹은 "기억하며 풀기" 라고 생각하면 쉽다 하였다.

우선, 주어진 길이가 $i$ 일 때, 그 때의 최대 수익인 $r_i$ 를 구해보자.
$r_1 = 1\\r_2=5\\r_3 = 8\\r_4 = 10$
이 될 것이다. $r_4$ 값을 어떻게 구했을까?

다음과 같이 가정해보자.

If optimal solution cuts the rod into $k$ pieces, for $1\le k \le n$ , maximum corresponding revenue is $r_n = p_{i_1}+p_{i_2}+\cdots+p_{i_k}$

길이가 $n$ 인 rod를 $k$ 개의 pieces로 나누고 이 때가 최적해라고 가정한다면, 길이 $n$ 은 다음과 같이 나타나게 된다.

n = i_1 + i_2 + \cdots + i_k

그럼, 최대 수익 $r_n$ 은 위 가정의 식처럼 될 것이다.

그럼 어떻게 $r_n$ 을 구할 수 있을까?

$p_n$ : 자르지 않는 경우의 가격
$r_1 + r_{n-1}$ : 길이가 1인 rod와 $n-1$ 인 rod로 나누는 경우의 최대 이익 (pieces들의 총 합이니까 두 값을 더해야한다.)
$r_2 + r_{n-2}$ : 길이가 2인 rod와 $n-2$ 인 rod로 나누는 경우의 최대 이익
$\cdots$ : 이와 같은 순서로 반복
$r_{n-1} + r_1$ : 마지막에는 길이가 $n-1$ 인 rod와 1로 나누는 경우가 될 것이다.

즉,

r_n = \max\{p_n, r_{1} + r_{n-1}, r_{2} + r_{n-2}, \cdots, r_{n-1} + r_{1} \}

이 된다. 이 때, 자르지 않는, (1.) 경우를 제외하고 $r$ 값이므로 각 subproblems들을 재귀적으로 해결한다는 것도 내포하고 있다. 더 간단하게 위 수식을 표현하면 다음과 같다.

r_n = \max_{1\le i\le n} \left(p+r_{n-i}\right)

하지만 이대로 recursive한 top-down 방식으로 문제를 해결하면 상당히 비효율적이다. 왜 그럴까? 당연히 상당히 많은 subproblems가 반복되기 때문이다. 즉, 중복된 연산이 많다. 예를 들어 $n=7$ 일 때, (1, 6)으로 나누고 (2, 5)로, (3, 4), ..., (6, 1)으로 나누었을 때의 최적해를 각각 구하게 되는데, 이 때 (2, 5)의 $r_5$ 를 구하는데 $r_2$ 와 $r_3$ 을 구했을 것이다. 하지만 이는 다시 (3, 4)의 $r_4$ 를 구하는데 $r_2$ 와 $r_3$ 을 또 계산하는 일이 반드시 발생하게 될 것이다. (재귀적으로 호출하니까) CUT-ROD 문제의 답을 구하는 pseudo code와 시간 복잡도를 계산해보면,

CUT-ROD(p, n)
if n==0
	return 0
q = -infinity // (음의 무한대)
for i = 1 to n
	q = max{q,p[i] + CUT-ROD(p, n-i)}
return q

재귀적으로 CUT-ROD가 호출되니까 $T(n)$ 은 다음과 같다.

T(n) = \begin{cases} 1&\text{if }n=0\\ 1+\sum^{N-1}_{i=0}T(i)&\text{if }n \ge 1 \end{cases}

시간 복잡도를 recursion tree로 계산해도 $T(n)=2^n$ 이고, subsitution method로 계산해보면, $T(n)=2^n$ 이라 가정하자. $n=0$ 일 때, $T(0)=1$ 이므로 참이다. $k\ge 1$ 일 때, $T(k) = 1+\sum 2^i=1+\left(2^k-1\right)/\left(2-1\right)=2^k$ 이므로, $n=k+1$ 에 대해서 구해보면,

\begin{aligned} T(k+1)&=1+\sum^{k}_{i=0}2^i\\ &=1+\frac{2^{k+1}-1}{2-1}=2^{k+1} \end{aligned}

이므로 $T(n)=2^n$ 임을 증명할 수 있다. 즉, $T(n) \in O(2^n)$ 이므로 상당히 시간이 오래 걸린다. 이대로 두면 비효율적이라는 것을 재확인할 수있다.

당연히 DP는 여기서 한가지 방법을 더 도입한다. 바로 이전의 연산 결과들을 저장하는 것이다. 이전에 계산한 subproblem의 optimal solutions들을 새로운 표(table)에 저장하는 것이다. 만약, 다른 subproblem을 풀다가 저장되어 있는 subproblem의 연산 결과가 필요하다면 표에서 가져오면 다시 연산을 수행할 필요가 없으니, 시간 복잡도는 감소할 것이다. 물론, "time-memory trade off" 관계에 의해 그만큼 추가적인 메모리가 필요하겠지만 확실히 시간 복잡도를 줄일 수 있다.

이렇게 기존의 연산 결과를 저장하며 재귀적으로 문제를 풀어가는 DP의 구현은 크게 2가지로 나뉜다.

Top-Down with Memoization
Bottom-Up method

사실 재귀 호출의 방식에 따라 구분하는 것이지 DP의 핵심 개념인 기존의 연산결과를 저장한다는 것은 둘 다 동일하다.

Top-down with Memoization

Memoization(이전의 연산 결과를 메모한다. 즉 저장한다) 방식으로 rod cutting problem을 해결하는 수도 코드는 위와 같다. 수도 코드를 보면, 우선 이전의 연산 결과, 길이가 $i$ 일 때의 최적의 해를 저장하기 위해 배열 $r$ 을 새로 정의하고, 만약 이전의 연산 결과가 저장 되어 있다면, 그대로 사용하고, 저장 되어 있지 않다면, 연산을 수행하는 방식(물론 연산 수행 후에 배열 $r$ 에 저장한다)이다.

시간복잡도는 문제의 크기에 도달할 때까지 $n$ 번 재귀 호출하고, 각 재귀 호출마다 for 반복문을 돌기 때문에, $O(n^2)$ 이라 할 수 있다.

Bottom-Up

bottom-up 방식도 동일하게 이전의 연산 결과를 저장하지만, 문제의 크기를 기준으로 오름차순으로 정렬된 순서로 계산해나가며 최종 최적 해를 구하는 방식이다. 이 경우, for 이중 반복문이 존재하기 때문에, 시간 복잡도는 $O(n^2)$ 라고 간단히 구할 수 있다.

Extended Bottom-Up

기존의 Bottom-Up 방식은 최적의 해인 $r_i$ 를 기록하는 방식이였는데, 이를 개선하기 위해 최적의 choice도 같이 기록하게끔 개선한 방법이다. 물론 rod를 자른 위치를 기록하기 위해 배열 $s$ 가 또 추가적으로 필요하게 된다.

답을 구할 때 편하기 위해 도입한 방식이지, 시간 복잡도는 동일하다.

정리

DP를 활용하면 기존의 방법으로 시간 복잡도가 $2^n$ 이였던 문제가 $n^2$ 로 줄어들게 되었다. 이렇듯 optical substructure를 가지는 문제를 풀 때 DP 알고리즘을 사용하면, 훨씬 효율적이라는 것을 알아보았다. 다음 시간에는 Matrix-Chain Multiplication 문제를 DP를 활용해 어떻게 풀 수 있는지를 알아보자.

jmt

고분자/컴공

이전 포스트

[알고리즘] 04. Divde and Conquer

다음 포스트