[leetcode] Longest Ideal Subsequence

문제

• 소문자 알파벳으로 이루어진 문자열 s와 정수 k가 주어진다.
• 아래를 만족하는 문자열을 t라고 정의한다.
  • t는 s의 subsequence이다. subsequence는 문자열에 있는 문자의 순서는 유지한 상태에서 특정 문자들을 선택적으로 지워서 만들 수 있는 문자열이다.
  • 인접한 두 문자에 대해 알파벳 순서 차이의 절댓값이 k보다 작거나 같아야 한다.
• 주어진 s와 k에 대해서, 가능한 t의 가장 긴 길이를 구해야 한다.
• 제약 조건
  • 문자열 s 길이: 1 <= s.length <= 10^5
  • k 범위: 0 <= k <= 25
• 예시
  

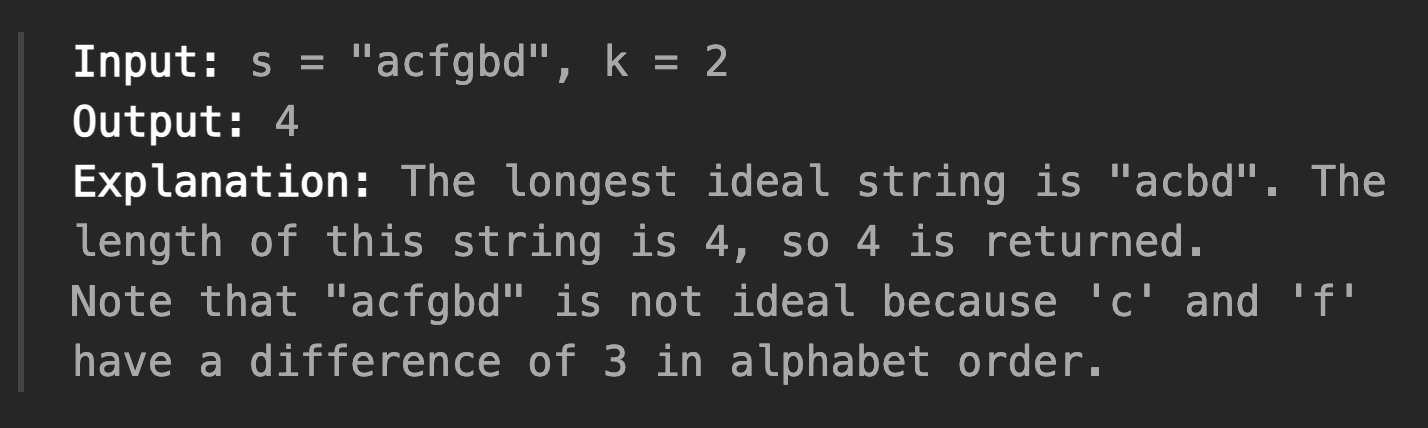
풀이

풀기 전

• 문자열 s의 길이가 최대 10만이기 때문에 브루트포스 방식으로는 어려울 거 같았다.
• 아무리 규칙을 찾아봐도 이렇다 할 규칙은 보이지 않았다. 그렇다면 남은 건 DP.. 머리가 아파져서 피하고 싶었지만 DP로 풀 수 밖에 없어 보였다.
• DP는 일단 이전에 계산한 결과를 저장한 뒤, 그 이후에 같은 계산이 필요할 때 저장한 값을 사용할 수 있어야 한다. 그렇다면 해당 문제에서 계산해둬야 하는 값은 무엇일까. 만약 문자열 s의 길이가 10이라면, 9번째 문자까지의 결과를 저장하여 사용할 수 있어야 한다. i번째 문자까지 가장 긴 t 길이를 구하려면, i-1번째 문자까지의 결과를 활용해야 한다는 거다.
• 그럼 어떤 값을 저장하고 활용해야 하는지 고민해봐야 한다. 어떤 값을 저장할지 두 가지를 생각해볼 수 있다. (1) k번째 문자에서 가장 긴 t 길이와 (2) 특정 문자에서 가장 긴 t 길이다. (1)은 시간 복잡도가 문자열 길이의 제곱만큼 늘어난다. i번째에서 가장 긴 t 길이를 구하기 위해 0 ~ i-1 인덱스를 순회하며 조건을 만족하는 문자 중에서 가장 큰 값에 1을 더한 뒤 i번째에 저장한다. (2)는 문자의 범위가 a~z뿐이라는 점을 이용한다. a~z를 0~25에 대응시킨 뒤, 특정 문자에서 가장 긴 t 길이를 저장한다. 이러면 시간 복잡도가 문자열 길이에 선형적으로 증가한다.
• 주어진 제약 조건에서는 (2)의 방법으로만 동작할 거 같다. 사실 (1) 방식은 DP라고 할 순 없을 거 같다.

코드

class Solution {
    public int longestIdealString(String s, int k) {
        char[] chars = s.toCharArray();
        
        // 인덱스는 문자를 의미한다.
        // 특정 문자에서 가질 수 있는 가장 긴 t의 길이를 저장한다.
        int[] prevLen = new int[26];
        
        for (int i=0; i<chars.length; i++) {
            char ch = chars[i];
            
            int upper = Math.min(ch + k - 'a', 25);  // 조건을 만족하는 문자의 상한선이다.
            int lower = Math.max(ch - k - 'a', 0);  // 조건을 만족하는 문자의 하한선이다.

            int tmp = 1;
            // 조건을 만족하는 문자들을 순회하면서 가장 긴 t 길이를 구한다.
            for (int j=lower; j<=upper; j++) {
                tmp = Math.max(prevLen[j] + 1, tmp);
            }
            prevLen[ch - 'a'] = tmp;  // 구한 값을 저장해준다.
        }

		// 모든 문자 중에서 가장 긴 t 길이를 가진 값을 반환한다.
        int ret = 0;
        for (int len : prevLen)
            ret = Math.max(ret, len);
        return ret;
    }
}

푼 후

• DP는 고민한 거에 비해 코드는 짧아서 좋으면서도 허무하다.
• 문자열 s의 길이를 n이라고 하면 시간 복잡도는 O(nk)라고 할 수 있다. 문자열을 순회하면서 최대 k 값의 두배만큼 문자들을 순회하기 때문이다. k 값이 25 이하라서 크게 차이는 없긴 하다. 문자열을 배열로 변환하여 사용하기 때문에 공간 복잡도는 O(n)이다. 문자열을 그대로 사용하면 상수 복잡도를 갖지만, 배열로 변환해서 사용하는 게 빨라서 바꿔줬다.