[leetcode] Minimum Falling Path Sum II

문제

• n x n의 이차원 정수 배열 grid가 주어진다. non-zero shift로 하강하는 경로의 합 중에서 가장 작은 값을 구해야 한다. non-zero shift라는 건 같은 열로 하강해서는 안 된다는 의미이다. 하강한다는 건 위쪽 행에서부터 아래쪽 행으로 내려가는 걸 의미한다.
• 제약 조건
  • n의 범위: 1 <= n <= 200
  • 값의 범위: -99 <= grid[i][j] <= 99
• 예시
  

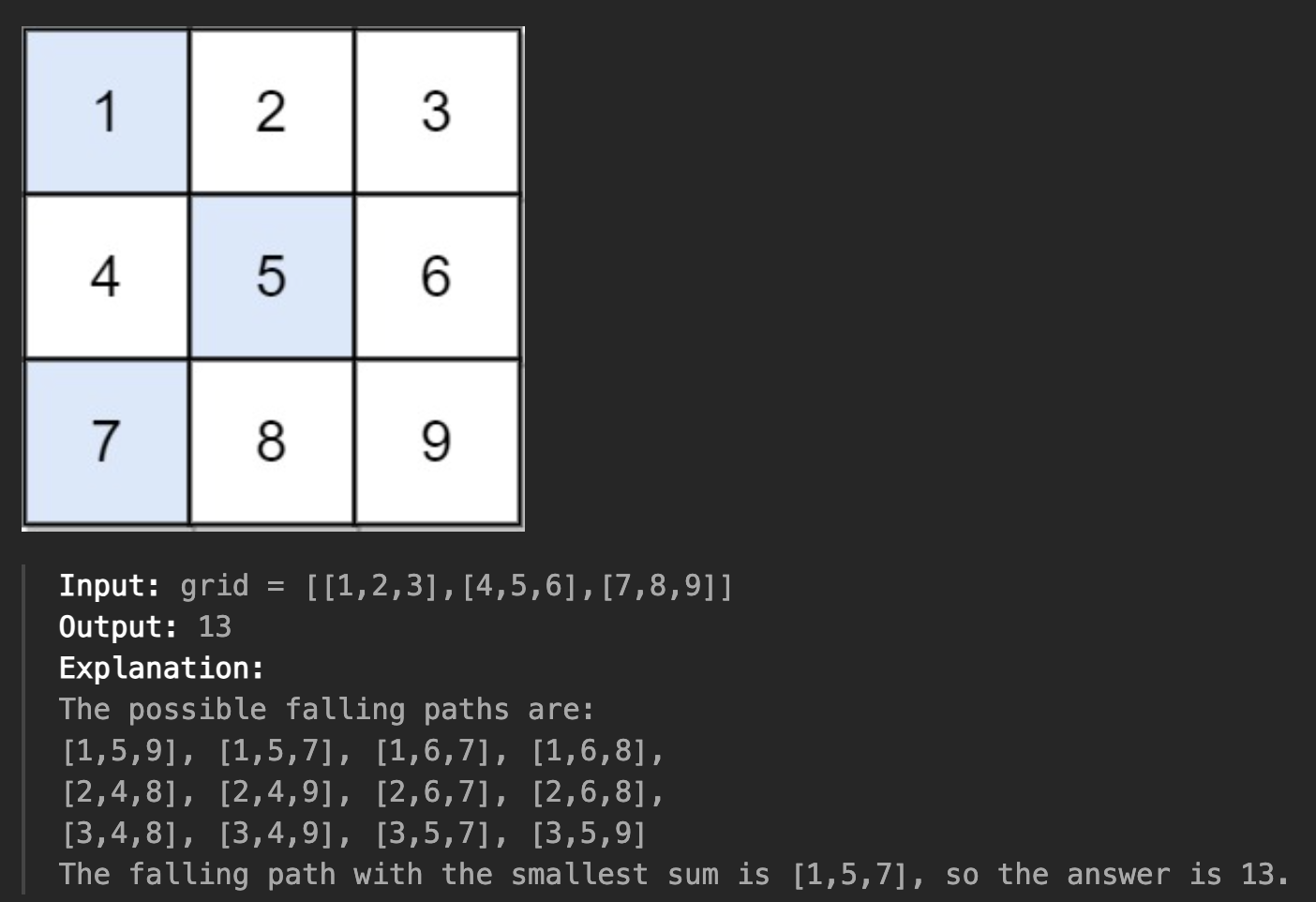
풀이

풀기 전

• DP처럼 보이는데 hard래서 좀 쫄았다.
• 처음에 떠오른 생각은 i번째 행에 있을 때, i-1번째 행에 있는 값 중에서 제일 작은 값을 누적해서 더해주면서 밑바닥 행까지 내려가는 방식이었다. grid를 순회하는 데에 n^2이고, 특정 값 위치에서 윗 행에 있는 값 중 열이 다른 최솟값을 구해준 뒤 더해줘야 하므로 총 시간 복잡도는 O(n^3)이 됐다. 안 되겠지 하면서 제약 조건을 봤는데 n이 200 이하여서 충분히 가능할 거 같았다. 가능하다는 기준은 대충 1억 번 이하의 연산으로 판단한다. 그래서 위 방식으로 풀었고 실제로 풀렸다.
• 위 방식을 조금 더 개선하면, 특정 값 위치에서 매번 윗 행의 최솟값을 구해줄 필요 없이, 미리 최솟값 두개까지만 구해주면 된다. 같은 열에 있지 않은 최솟값을 사용하려면 2개까지만 구하면 되기 때문이다. 이렇게 개선하면 시간 복잡도는 O(n^2)이 된다.

코드

class Solution {
    public int minFallingPathSum(int[][] grid) {
        int n = grid.length;

        for (int i=1; i<n; i++) {  // 0번째 행은 그대로 두면 되므로 1행부터 시작한다.
        	// 첫번째 최솟값과 두번째 최솟값을 저장할 배열이다.
            int[][] mins = {{-1, Integer.MAX_VALUE}, {-1, Integer.MAX_VALUE}};
            
            // 두 최솟값을 구해준다.
            for (int j=0; j<n; j++) {
                int val = grid[i-1][j];
                if (val < mins[0][1]) {  // 최솟값보다 작으면 갱신해준다.
                	// 기존의 최솟값은 두번째 최솟값으로 옮긴다.
                    mins[1][0] = mins[0][0];
                    mins[1][1] = mins[0][1];
                    
                    // 최솟값 갱신한다.
                    mins[0][0] = j;
                    mins[0][1] = val;
                } else if (val < mins[1][1]) {  // 두번째 최솟값보다 작으면 갱신해준다.
                    mins[1][0] = j;
                    mins[1][1] = val;
                }
            }

            for (int j=0; j<n; j++) {
                if (j != mins[0][0])  // 열이 다르면 첫번째 최솟값을 사용한다.
                    grid[i][j] += mins[0][1];
                else  // 열이 같으면 두번째 최솟값을 사용한다.
                    grid[i][j] += mins[1][1];
            }
        }

		// 밑바닥 행에 있는 값 중에 최솟값을 반환한다.
        int ret = Integer.MAX_VALUE;
        for (int i=0; i<n; i++)
            ret = Math.min(ret, grid[n-1][i]);
        return ret;
    }
}

푼 후

• n 크기의 반복문 2개가 중첩되고 있으니 시간 복잡도는 O(n^2)이다. 주어진 grid 외에 상수 공간만 추가되었으니 공간 복잡도는 O(1)이다.