Merge Sort

병합 정렬이란

---

분할 정복 알고리즘 기법을 사용하는 정렬 방법이다.
정렬할 데이터를 작은 단위로 분할 후, 다시 정렬하며 병합한다.

분할을 할 때는 정렬을 고려하지 않고 그저 분할만 진행하고
병합을 할 때 정렬순서를 고려하여 병합을 한다.

(이는 재귀적 알고리즘으로 이루어진다.)

병합 정렬 과정

---

그림 출처

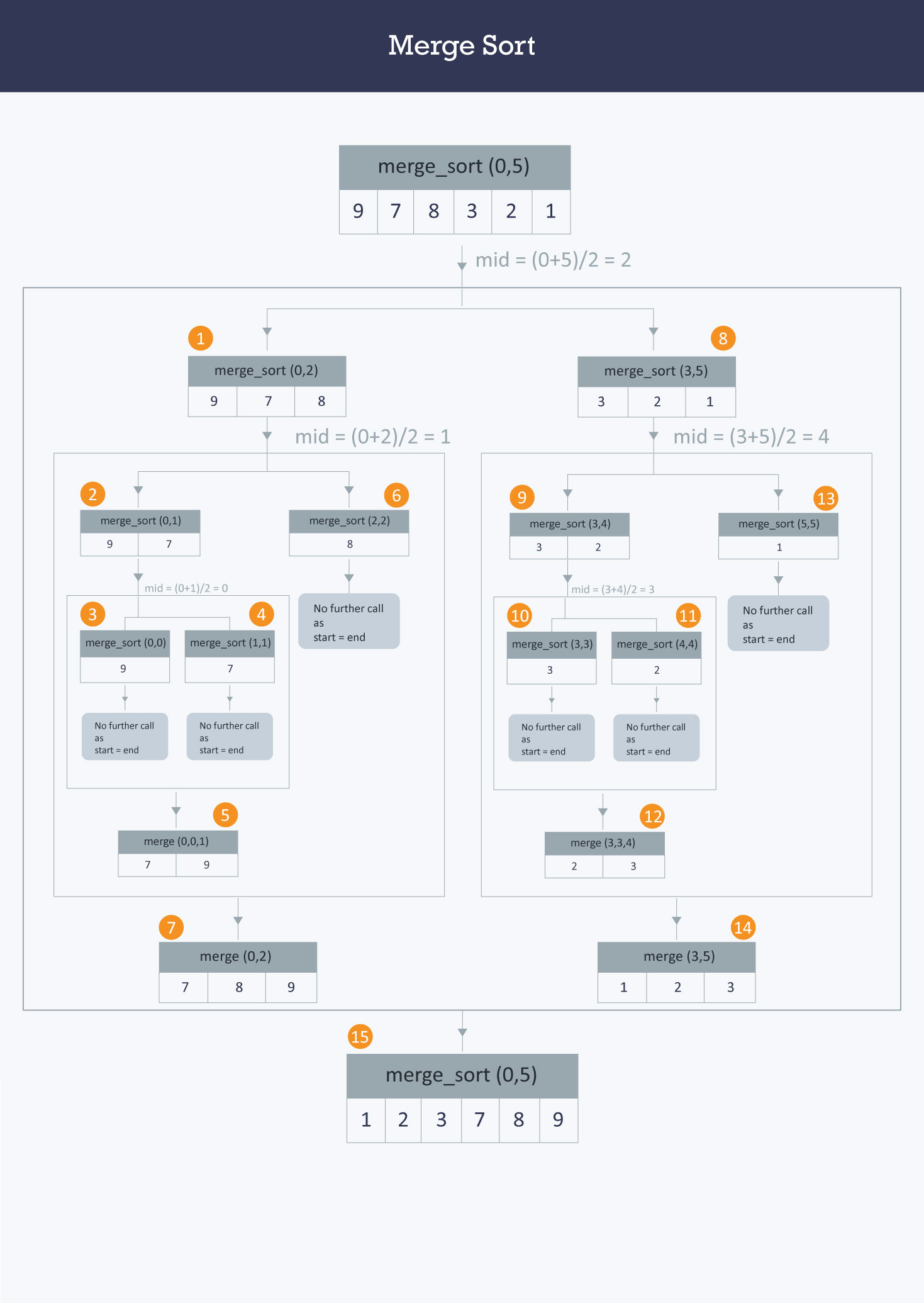
데이터를 반복적으로 더 이상 분할할 수 없는 단위가 될 때 까지 중간값(mid = first index + last index / 2)을 기준으로 분할한다.

분할이 완료되면 병합을 진행하는데 이때 우선 순위에 맞춰 합쳐진다.
모든 부분 배열이 병합되면 최종적으로 전체 배열이 정렬된다.

구현

---

아래는 c언어로 구현된 병합 정렬 입니다.

// C program for Merge Sort
#include <stdio.h>
#include <stdlib.h>

// Merges two subarrays of arr[].
// First subarray is arr[l..m]
// Second subarray is arr[m+1..r]
void merge(int arr[], int l, int m, int r)
{
    int i, j, k;
    int n1 = m - l + 1;
    int n2 = r - m;

    // Create temp arrays
    int L[n1], R[n2];

    // Copy data to temp arrays L[] and R[]
    for (i = 0; i < n1; i++)
        L[i] = arr[l + i];
    for (j = 0; j < n2; j++)
        R[j] = arr[m + 1 + j];

    // Merge the temp arrays back into arr[l..r
    i = 0;
    j = 0;
    k = l;
    while (i < n1 && j < n2) {
        if (L[i] <= R[j]) {
            arr[k] = L[i];
            i++;
        }
        else {
            arr[k] = R[j];
            j++;
        }
        k++;
    }

    // Copy the remaining elements of L[],
    // if there are any
    while (i < n1) {
        arr[k] = L[i];
        i++;
        k++;
    }

    // Copy the remaining elements of R[],
    // if there are any
    while (j < n2) {
        arr[k] = R[j];
        j++;
        k++;
    }
}

// l is for left index and r is right index of the
// sub-array of arr to be sorted
void mergeSort(int arr[], int l, int r)
{
    if (l < r) {
        int m = l + (r - l) / 2;

        // Sort first and second halves
        mergeSort(arr, l, m);
        mergeSort(arr, m + 1, r);

        merge(arr, l, m, r);
    }
}

// Function to print an array
void printArray(int A[], int size)
{
    int i;
    for (i = 0; i < size; i++)
        printf("%d ", A[i]);
    printf("\n");
}

// Driver code
int main()
{
    int arr[] = { 12, 11, 13, 5, 6, 7 };
    int arr_size = sizeof(arr) / sizeof(arr[0]);

    printf("Given array is \n");
    printArray(arr, arr_size);

    mergeSort(arr, 0, arr_size - 1);

    printf("\nSorted array is \n");
    printArray(arr, arr_size);
    return 0;
}

성능평가

---

정렬 해야할 Data가 $N$개 일 때 배열을 반복적으로 절반씩 나누는 과정에서 $\log_2n$의 시간이 소요되고, 각 병합단계에서 $n$개의 요소를 비교해야 하기 때문에
시간복잡도는 $O(nlog_2n)$ 입니다.

장점

---

• Stability : 동일한 값을 가진 요소들의 순서가 유지된다.

• Guaranteed worst-case performance : 시간 복잡도 $O(n\logn)$을 항상 보장하므로, 최악의 경우에도 효율적이다.

• Simple to implement

• Naturally Parallel : 분할된 배열을 독립적으로 처리할 수 있어 병렬 처리가 가능하다.

단점

---

• Space complexity: 추가적인 메모리가 필요하다. 각 단계에서 임시 배열을 사용하여 데이터를 저장해야 하기 때문에 메모리 사용이 크다.

• Not in-place 정렬이다.

정리

---

이러한 병합 정렬은 대규모 데이터 정렬에 유용하며 Python, Java Android and Swift와 같은 언어의 library methods에서 변형된 상태로 사용됩니다.

특히 TimSort는 병합 정렬의 변형으로, 비원시 타입(Object, array 등)을 정렬할 때 자주 사용된다.