자료구조 / 알고리즘 (C)
1.자료구조와 알고리즘의 이해

Linear, binary, Big-Oh
2.재귀

재귀 함수
3.singly Linked List
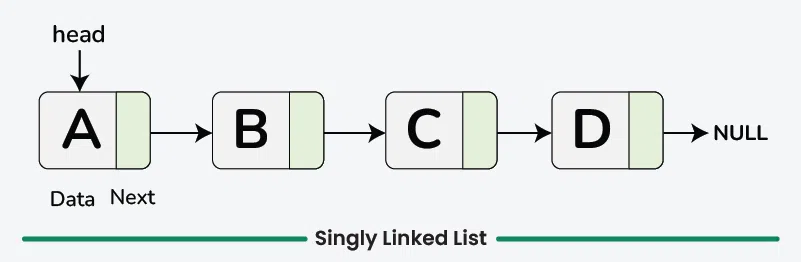
추상 자료형 (Abstract Data Type) 추상 자료형, ADT라고도 하는 이것은 구체적인 기능의 완성과정을 언급하지 않고, 순수하게 기능이 무엇인지를 나열한 것입니다. 지갑을 예시로 ADT를 설명해보면 지갑의 기능은 카드를 넣고, 빼거나 동전, 지폐등을 넣
4.Doubly Linked List
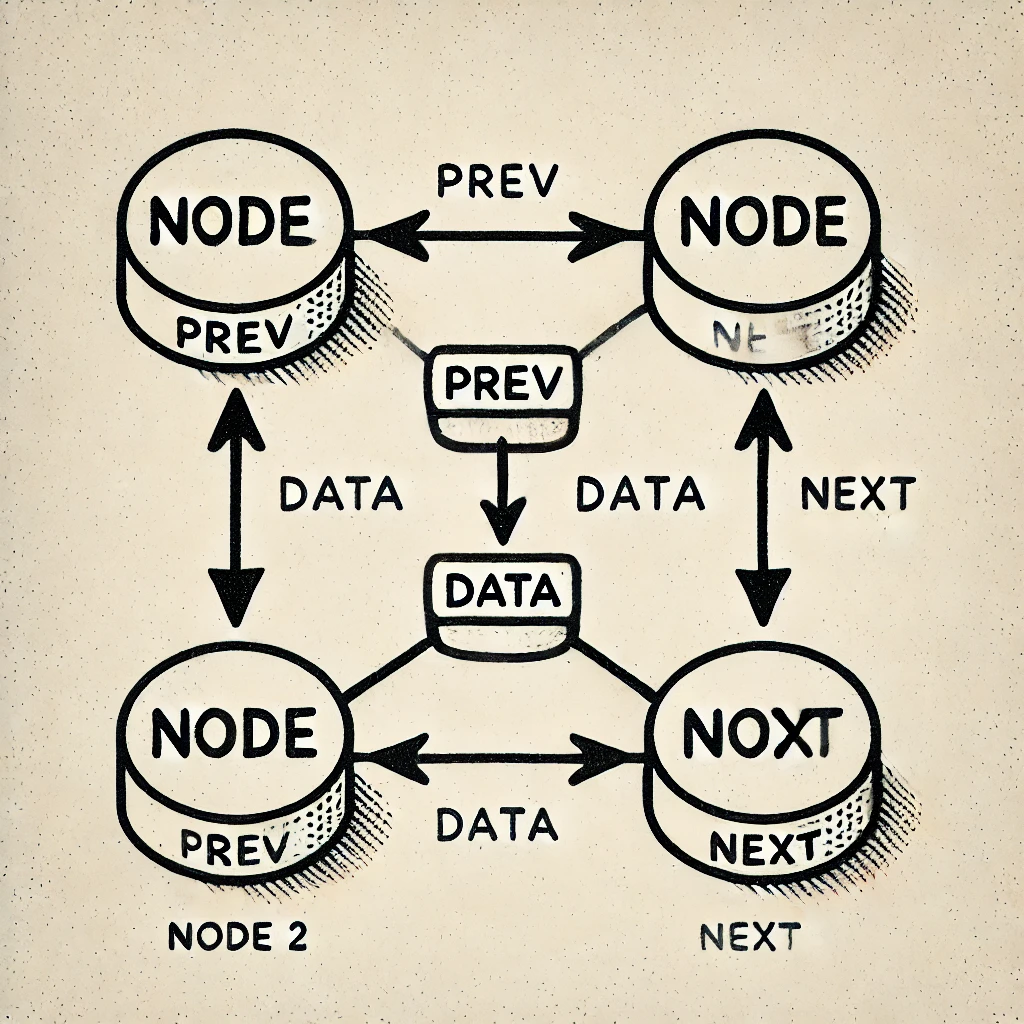
A doubly linked list is a type of linked list in which each node contains 3 parts, a data part and two addresses, one points to the previous node and
5.Stack

스택은 후입선출(LIFO, Last In First Out) 구조의 자료구조로, 들어간 순서의 역순으로 요소가 나옵니다.스택의 ADT(Abstract Data Type) 정의는 다음과 같습니다:ADT의 정의는 위와 같고 헤더파일을 디자인 하기전에스택은 배열과 연결 리스
6.Queue

큐 (Queue) 큐는 선입선출(FIFO, First-In-First-Out) 방식으로 작동하는 자료구조로 먼저 들어간 데이터가 먼저 나오는 구조로, 실생활에서 줄서기와 같은 상황을 떠올리면 쉽게 이해할 수 있습니다. 큐의 ADT (추상 자료형) 큐의 구현 큐는
7.Hash Map / Table

해시맵(Hash Map)은 키-값(key-value) 쌍을 저장하는 자료구조입니다. 키를 통해 값을 빠르게 찾을 수 있도록 설계되어 있으며, 해시 함수를 사용해 데이터를 저장하고 검색합니다. 해시맵은 배열 기반의 자료구조이지만, 해시 함수를 통해 데이터를 일정한 크기의
8.순차 탐색과 이진 탐색 알고리즘

(Binary Search)배열에 저장된 정렬된 데이터를 대상으로 적용 가능하다.반씩 덜어내며 target값과의 비교를 통해 target값을 찾을때 까지 계속해서 반으로 덜어낸다.이진 탐색 알고리즘 구현first는 탐색 대상의 시작 인덱스 값이다. (idx는 0부터)l
9.버블 정렬 알고리즘

버블 정렬(Bubble Sort) 알고리즘은 서로 인접한 두 원소를 비교하여 정렬하는 알고리즘입니다. 선택 정렬(Selection Sort)과 기본 개념이 유사하지만, 매 회전(iteration)마다 가장 큰 값이 배열의 끝으로 이동한다는 특징이 있습니다.버블 정렬은
10.브루트 포스 알고리즘

문제를 해결하기 위해 가능한 모든 경우의 수를 탐색하는 방법직관적이고 간단하지만 하나씩 경우의 수를 체크하므로 비효율적일 수 있다.단순함 : 복잡한 알고리즘을 이해하지 않고도 쉽게 구현할 수 있으며 문제를 해결하는 데 있어서 모든 경우의 수를 고려하기 때문에 매우 직관
11.Quickselect Algorithm

Quickselect Algorithm은 선택 알고리즘 중 하나로, 주어진 배열에서 k번째로 큰(또는 작은) 요소를 찾는 데 사용됩니다.퀵 셀렉트는 퀵 정렬(Quicksort)에서 사용하는 분할 방식(Partitioning)을 응용하여 목표로 하는 k번째 요소를 빠르게
12.Selection Sort

정렬순서에 맞게 하나씩 선택해서 옮기는, 옮기면서 정렬이 되게 하는 알고리즘이다.정렬순서상 가장 앞서는 것을 선택해서 가장 왼쪽으로 이동시키고, 원래 그 자리에 있던 데이터는 빈 자리에 가져다 놓는다.반복문 부분을 확인해보면시간복잡도 : $O(n^2)$
13.Insertion Sort

삽입 정렬 정렬 대상을 두 부분으로 나눠서, 정렬 안 된 부분에 있는 데이터를 정렬 된 부분의 특정 위치에 삽입해가면서 정렬을 진행하는 알고리즘이다. https://www.hackerearth.com/practice/algorithms/sorting/insertio
14.Divide and Conquer

분할 정복(Divide and Conquer) 알고리즘은 문제를 더 작은 하위 문제들로 분할하고, 각 하위 문제를 해결한 후, 그 결과를 결합하여 전체 문제를 해결하는 알고리즘 전략입니다. 이 방법은 재귀적으로 문제를 해결하며, 많은 복잡한 문제들을 효율적으로 해결할
15.Merge Sort
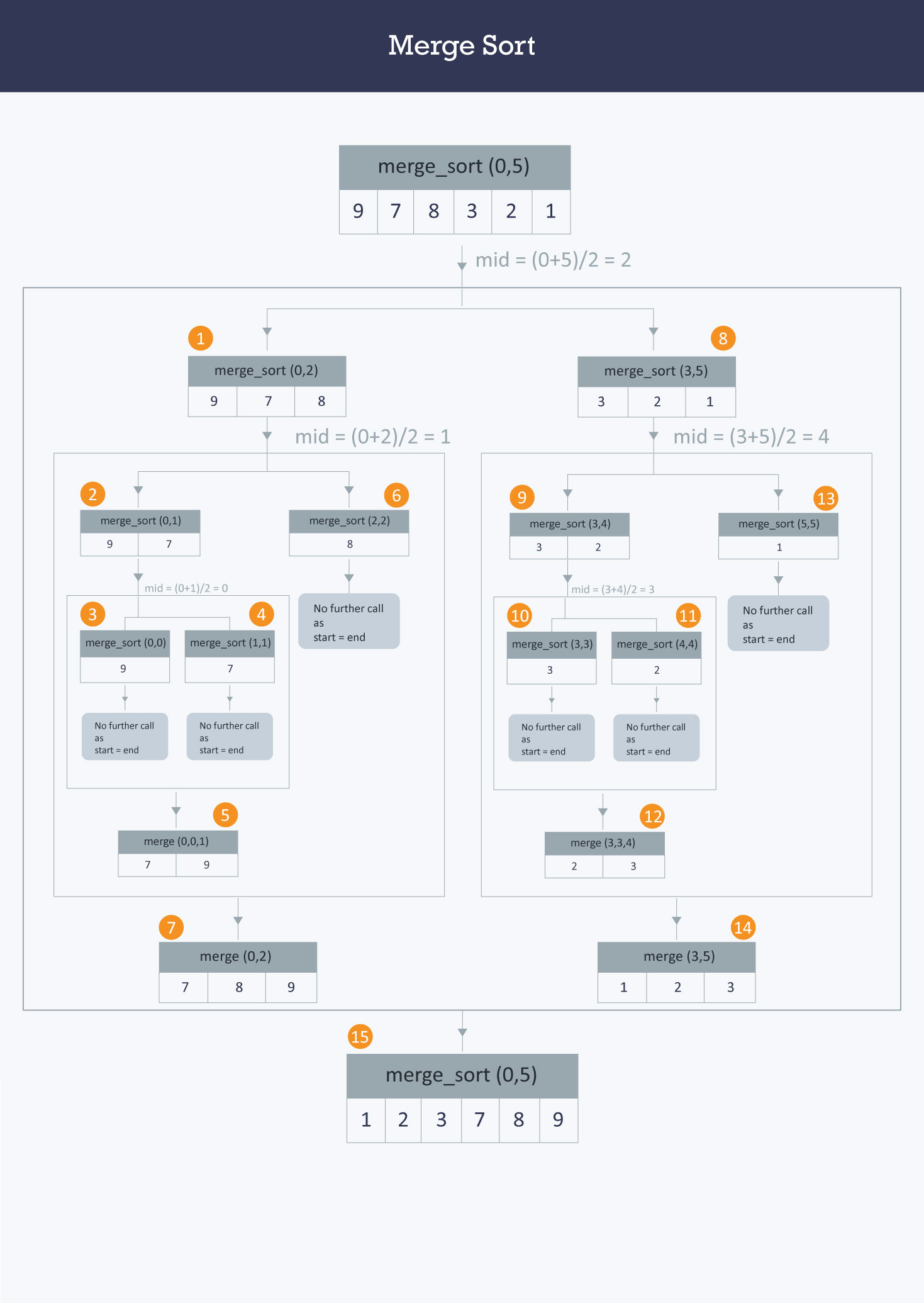
분할정복 알고리즘 디자인 기법에 근거하여 만들어진 정렬 방법.정렬 할 데이터를 정렬하기 쉽게 가장 작은 단위로 분할을 하는데분할을 할 때는 정렬을 고려하지 않고 그저 분할만 하면된다.분할이 끝나면 병합을 하는데 정렬순서를 고려하여 병합을 한다.위와같이 재귀적인 알고리즘
16.Quick Sort
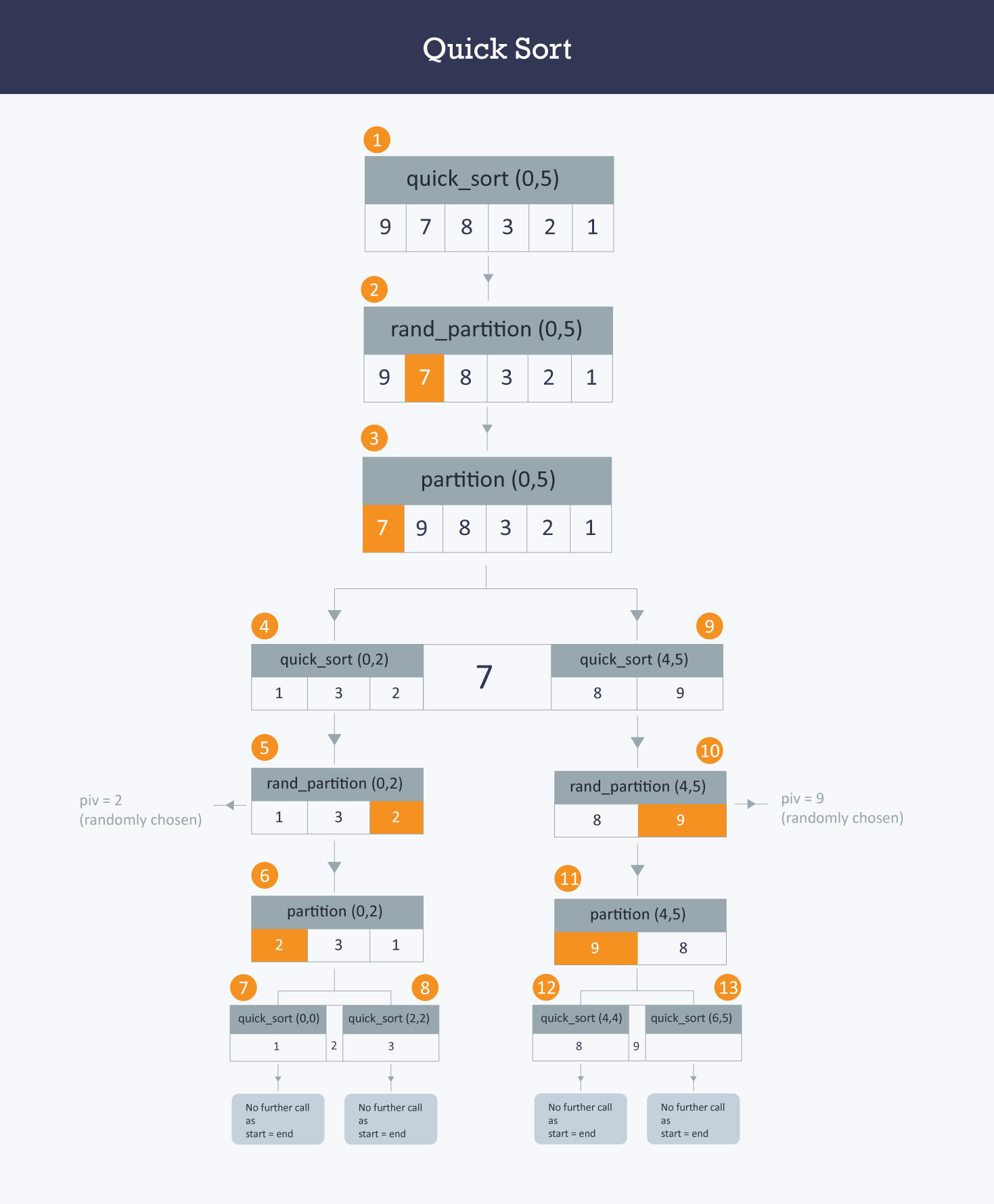
퀵 정렬은 분할 정복(Divide and Conquer) 알고리즘의 일종으로, 평균적으로 $O(n \\log n)$의 시간 복잡도를 가지는 매우 효율적인 정렬 알고리즘이다.퀵 정렬은 피벗(Pivot)이라는 기준점을 선택한 후, 피벗보다 작은 요소들은 왼쪽에, 큰 요소들
17.Counting Sort

카운팅 정렬은 비교 기반이 아닌 분포 기반의 정렬 알고리즘입니다. 정렬하려는 데이터의 크기가 제한적일 때 매우 효율적으로 동작하며, 시간 복잡도가 $O(n)$입니다.특히 정렬할 데이터의 범위가 좁고, 데이터가 중복되어 있을 때 강력한 성능을 발휘합니다.시간 복잡도: $
18.Heap Sort
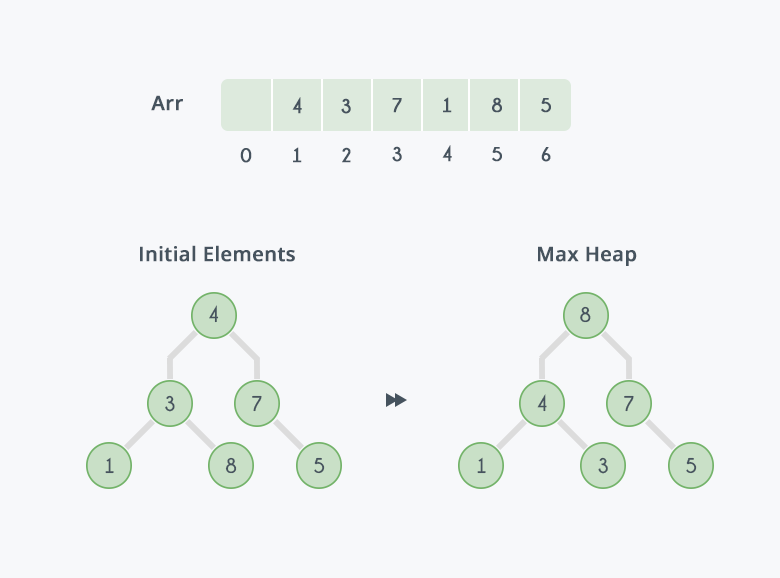
자료구조인 heap을 정렬을 기반으로한 정렬 알고리즘으로max-heaps에서 root node가 가장 큰 값이라는 점을 이용하여 정렬을 수행합니다.정렬 과정을 그림과 함께 이해하는것이 빠른데Heap Sort 그림 출처먼저 array에 있는 값들을 max-heap으로 변
19.Radix Sort

기수 정렬은 숫자를 구성하는 각 자릿수를 기준으로 정렬하는 선형 정렬 알고리즘으로 크기가 고정되어있는 문자나 숫자 정렬에 유용합니다.설명을 위해 {170, 45, 75, 90, 803, 24, 2, 66} 라는 배열이 있다고 가정하고그림 출처해당 배열에서 자릿수가 가장
20.Interpolation Search

보간 탐색(Interpolation Search)은 이진 탐색의 변형으로, 특정 값의 위치를 예측하여 탐색하는 알고리즘입니다.이진 탐색이 중간값(mid)을 기준으로 배열을 나누는 반면, 보간 탐색은 배열의 값 분포를 고려하여 탐색할 위치를 추정합니다.실생활에서 자주 사
21.Binary Search
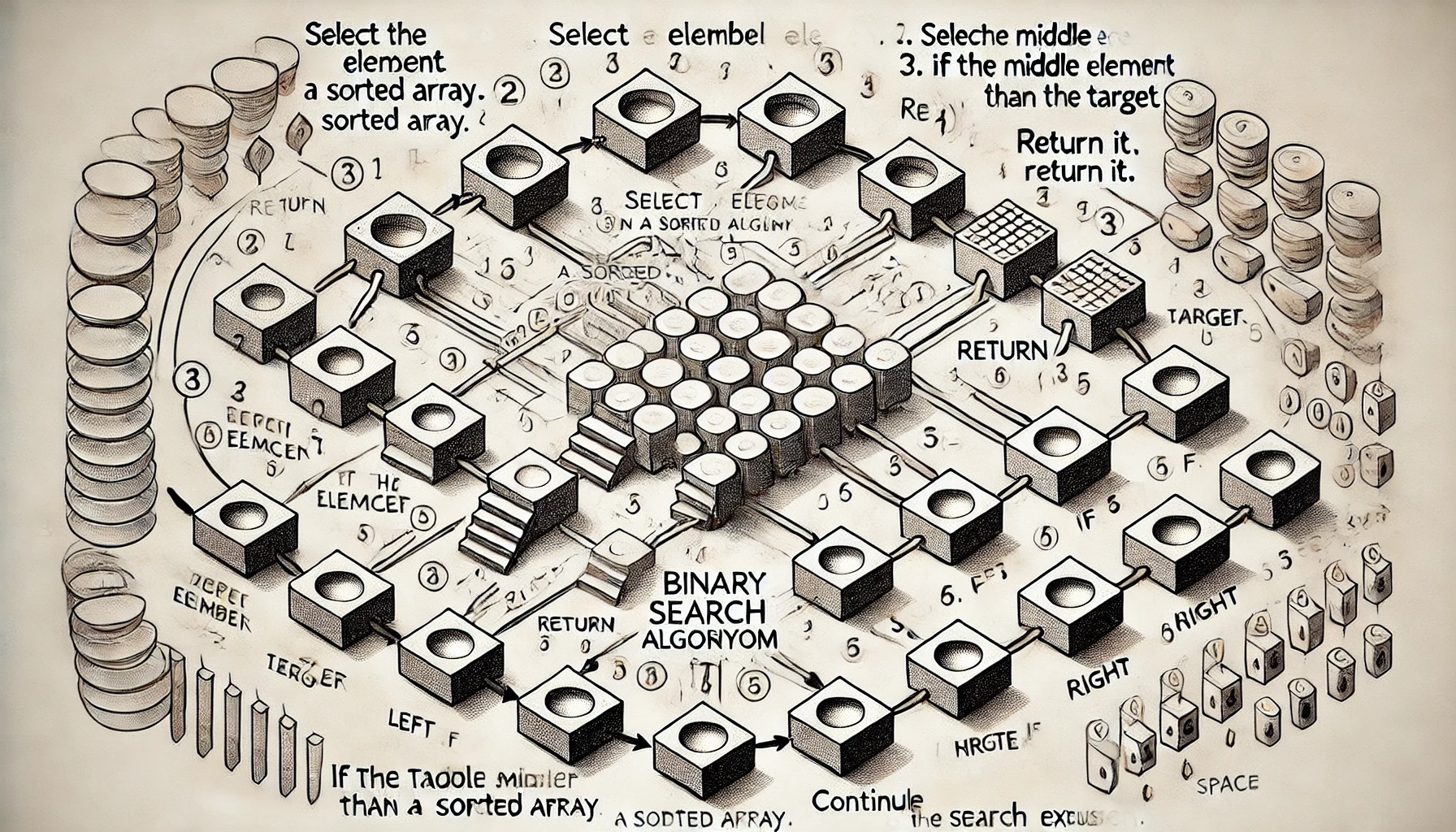
이진 탐색은 정렬된 데이터에서 중간값(mid)을 선택한 후, 목표값과 비교하여 데이터의 절반을 제거하는 방식으로 탐색 범위를 좁혀가는 탐색 알고리즘입니다.이 과정을 반복하여 목표값을 찾거나, 찾을 수 없는 경우 탐색을 종료합니다.이미지 출처중간값 선택: 먼저 배열의 가
22.Ternary Search

삼진탐색은 이진탐색과 같은 분할정복 알고리즘 탐색방법이며 이진탐색과 다른점은 탐색 대상을 세 부분으로 나누어 탐색합니다. 이진탐색과 마찬가지로 정렬된 데이터를 대상으로만 사용 가능합니다. 이진탐색에서 mid값을 기준으로 분할하였듯 삼진탐색에서는 mid1, mid2
23.Graph

그래프는 정점(Vertex)과 간선(Edge)으로 이루어진 자료구조로, 정점 간의 관계를 나타내는 데 사용됩니다.그래프는 네트워크, 소셜 관계, 경로 탐색, 작업 스케줄링 등 다양한 문제를 모델링하는 데 필수적인 구조입니다.정점(Vertex): 그래프를 구성하는 개체.
24.Graph Algoltim

그래프 알고리즘들최소 신장 트리(Minimum Spanning Tree)는 가중치 그래프에서 모든 정점을 연결하면서, 간선의 가중치 합이 최소가 되는 트리를 의미합니다. 최소 신장 트리는 다음 두 가지 알고리즘으로 구할 수 있습니다.작동 방식:모든 간선을 가중치 기준으
25.Eulerian Path

오일러 경로(Eulerian Path)는 그래프 내의 모든 간선을 정확히 한 번씩 통과하는 경로를 의미합니다.만약 이러한 경로가 시작 정점과 종료 정점이 동일하다면, 이를 오일러 회로(Eulerian Circuit)라 합니다.오일러 경로와 회로는 그래프 이론에서 매우
26.Red Black Tree

일반적인 이진 검색 트리(BST)는 평균적으로 $O(log N)$의 시간 복잡도를 가지지만, 최악의 경우 편향 트리(한쪽으로 치우침)가 되어 $O(N)$의 성능을 보이는데, RB Tree는 이러한 문제를 해결하여 최악의 경우에도 $O(log N)$을 보장하는 자료구조이
27.B tree
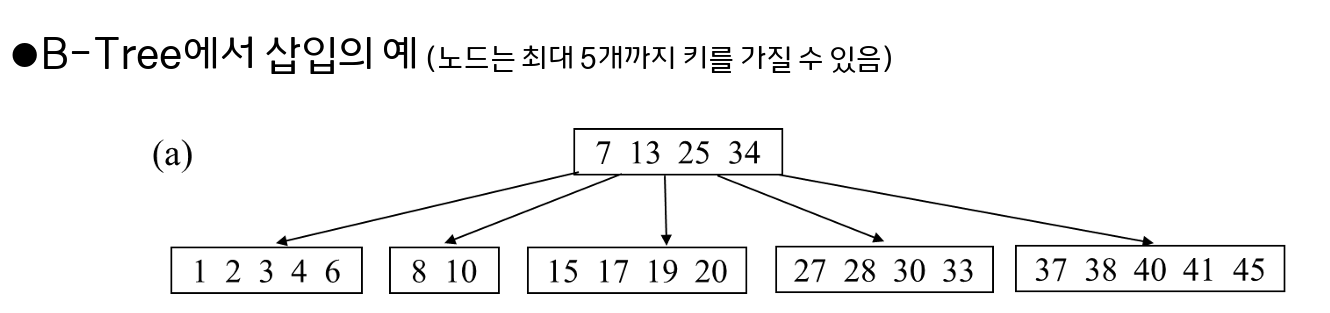
이진탐색트리(BST)를 일반화한 트리로 B-tree는 다진검색트리가 균형을 유지함으로 최악의 경우 디스크 접근 횟수를 줄이고자 하는 트리의 형태이다. 특징 부모 노드는 자식 노드를 2개 이상 가질 수 있다. 루트를 제외한 모든 노드는 x개의 키를 갖는다. 노드가 자녀를 x개 가졌다면, key는 x-1개를 가진다. 노드 내의 key는 오름차순으로...
28.Multidimensional Search Tree
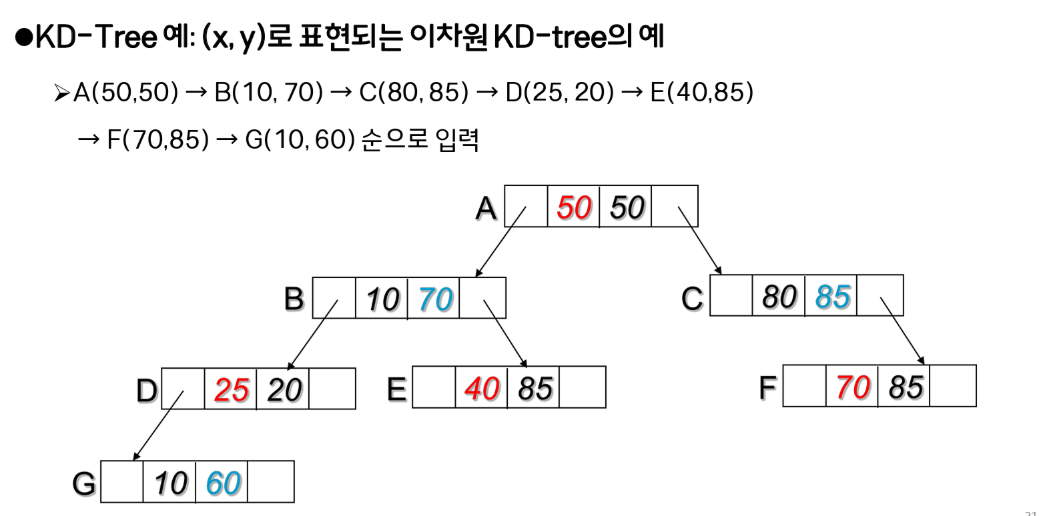
기존 검색 트리(BST, RB Tree, B-Tree)에서는 코드를 식별하는 검색 키(Key)가 하나로 이루어져 있었다. 하지만 지도 상의 위치를 나타내는 $(x, y, z)$ 좌표처럼 여러 속성을 복합적으로 다뤄야 하는 경우에는 일차원 검색트리를 사용할 수 없게된다. 이를 보완하기 위해 나온것이 다차원 검색트리이다. 다차원 검색트리는 KD-Tree...
29.Union-find Data Structure (Disjoint Set)
정의 Union-find는 disjoint set들을 관리하기 위한 data structre로서, 아래 3개의 operation을 지원한다. makeset(x): 단일 element x로 이루어진 set을 하나 생성한다. find(x): x가 포함된 set을 return한다. union(x, y): x가 포함된 set과 y가 포함된 set을 하나의...