예측적 데이터 분석 (Predictive Data Analysis)
- 목표변수와 설명변수 간의 관계를 수식화하여, (modeling) 새로 등장할 데이터를 예측하거나 대응
- 전통 통계 : 회귀분석 (모집단 추정)
- 데이터 마이닝 : 모집단 추정이라는 개념을 사용하지 않는다 / 학습
- 검증하는 단계가 있다
- 전통 통계에서 말하는 회귀분석과 데이터 마이닝의 회귀분석은 다른 매커니즘을 가진다
- 전통 통계 : 학습 / 검증을 나누지 않고 <-> 데이터 마이닝 : 모집단 추정하는 개념이 없다
전통 통계 회귀 분석
- 전통 통계 회귀 분석 절차
- 연속형 자료 간 상관분석 실시
- 변수가 산점도 확인을 통해 경향성을 확인 (비례 / 반비례)
- 상관관계 분석
- 목표변수와 설명변수 선택, 회귀 모델 구성
- 최소제곱법 사용
- 회귀모델의 적합성 확인
- 추정된 표준 오차 확인, 설명력을 나타내는 결정계수 확인
- 모델 유형의 적합성을 나타내는 ANOVA 분석결과 확인
- 회귀 계수 계산
- 선정된 회귀 모델에 대한 회귀계수를 계산
- 회귀계수의 유의성을 검정하고, 영향을 미치는 인자를 선정
- 오차(잔차)의 가정 확인
- 오차 = 실제 데이터 - 예측 데이터 : 회귀선으로 예측한 값
- 오차의 기본 가정사항을 확인 (오차의 정규성, 등분산성, 독립성)
- 모델 선정
- 연속형 자료 간 상관분석 실시
상관분석
- 두 변수간의 관계의 전반적인 윤곽을 확인
- Correlation Coefficient : X와 Y의 상관의 크기 - 비례 / 반비례 정도를 나타냄
- 시각화 방법을 통한 확인 : scatter
px.scatter(df1, x = 'Mean Compactness', y = 'Mean Concavity', color = 'Diagnosis',
trendline = 'ols')- 상관계수 확인 : .corr()
- -1~1 사이의 값
df1[['Mean Compactness', 'Mean Concavity']].corr()- 가설검정 (연속 - 연속)
- 정규성 확인 후
- 모두 정규성을 띈다면 : pearsonr
- 하나라도 정규성을 띄지 않는다면 : pearmanr
- 정규성 확인 후
전통 통계 회귀분석 실습
import statsmodel.api as sm
# X와 Y를 설정
X = df1['Mean Compactness']
Y = df1['Mean Concavity']
# constant 추가 (경향성)
X_const = sm.add_constant(X)
X_const
# 1로 가득 찬 컬럼을 생성- sm모델은 절편을 추가하지 않는 것이 디폴트이기 때문에 상수항, constant를 추가하여 절편값을 계산해줘야 함
- 이후 회귀분석 모델 생성
model = sm.OLS(Y, X_const) # 예측값, 절편
result = model.fit() # 학습
result.summary() # 결과 요약
모델 적합성 확인
- 통계 분석의 모집단에 대한 추정이 정확하려면, 통계적 관점에서 모델 적합성이 모두 만족해야 정확한 모델이라고 판단
- 적은 데이터로 추정하기 때문에 여러 지표로 꼼꼼하게 본다
- R² ( R square : 결정 계수)
- 0에서 1 사이의 값을 가진다
- 1 = 회귀선이 데이터를 완벽하게 설명
- 0 = 회귀선이 데이터를 전혀 설혀 설명하지 못함
- 0.78 : 78% 만큼 회귀선이 데이터를 설명한다 / 나머지 22%는 회귀선이 설명하지 못하는 부분
- adj R² (Adjusted R Square : 수정 결정 계수)
- 단일 변수로 예측할 땐 안봐도 된다
- 다변수로 회귀분석을 하는 경우 봐야한다
- 다중회귀분석 (변수 여럿으로 예측)을 할 때, X가 많아지면 R²가 오르는데, 이때 유의하지 않은 변수들이 추가될 수 있음
- 따라서 다중회귀분석에서 최적모형 선정기준으로 R²가 아닌 adj R²를 본다.
- R square와 adj r square가 10%이상 차이가 난다면, 너무 많은 변수들이 추가된 것이 아닌지 의심해볼 필요가 있음 (그래서 규제항을 추가하거나, 전진/후진 제거법으로 변수를 제거해나감)
- F-statistic (p value)
- 귀무가설 : 모델의 회귀계수가 모두 0이다.
- 대립가설 : 모델의 회귀계수 중 적어도 하나는 0이 아니다.
- 해당 회귀식이 기울기가 있는지, 회귀선이 특정 경향성을 따르는지에 대한 검정 결과
- log-likelihood : 우도 : 통계 모델의 적합도를 나타내는 척도
- 변수 θ가 주어졌을 때, 데이터 x가 발생할 확률
- 우도 <-> 확률변수
- 주사위라는 확률변수는 각 눈이 나올 확률이 1/6이다
- 우도 : 주사위 눈이 4가 관측됐을 때, 이 4가 1/6 확률을 가지는 주사위에서 나왔을 정도를 측정
- AIC (Akaike Information Criterion) : 모델의 적합도와 모델의 복잡성을 동시에 고려하여 모델을 비교하는 통계적 기준
- BIC (Bayesian Information Criterion) : 모델의 적합도와 복잡성을 고려하여 모델을 비교하는 데 사용되는 통계적 기준
- AIC는 데이터가 상대적으로 적거나, 예측 성능을 우선시 하는 경우 유용
- BIC는 데이터가 많고, 모델의 복잡성에 대해 더 강력한 제어가 필요할 때 유용
- 모델 간 유의성을 비교할 때 사용
- Covariance Type : Non Robust : 이상치에 민감
- 공분산 행렬 유형 : 전통적인 최소제곱법을 사용하여 공분산을 추정한다는 의미
- full / tied / diag / spherical
- const : 절편
- mean compactness coef : 기울기
- P > |t| : (t통계량) 해당 회귀 계수값이 유의미한가?에 대한 p value
- 귀무가설 : 회귀 계수는 0이다 / 대립가설 : 회귀 계수는 0이 아니다
- Omnibus 검정 : 회귀 모델 전체가 유의미한가?
- 모델의 적합성에 대한 종합적인 통계량을 제공하며, F검정을 기반으로 함
- 옴니버스 검정이 유의하면, 적어도 하나의 독립 변수가 종속 변수에 유의미한 영향을 미친다는 것을 나타냄
- p value 는 작을수록, 통계량은 클수록 X가 Y를 잘 설명
- 귀무가설 : 해당 모델은 데이터에 적합하지 않다
- 대립가설 : 해당 모델은 데이터에 적합하다
- Durbin-Watson 검정 : 회귀 모델의 오차항 간의 자기상관을 평가하는 검정
- 자기상관이 존재하면 모델의 표준 오차가 편향될 수 있으며, D-W 통계량은 이를 평가하는데 사용
- 오차 편향 여부 : 데이터가 회귀선으로부터 고르게 퍼져있나 아닌가
- 오차가 편향됐다 = 설명변수X가 아닌 다른 요인에 의해 회귀식이 영향을 받는다
- 0~4 사이의 값을 가진다
- 0 = 양의 자기 상관 / 4 = 음의 자기상관을 가질 가능성을 높다
- Jarque-Bera (JB) 검정 : 회귀 모델의 오차항이 정규분포를 따르는지를 검정
- p value : 귀무가설 : 오차항은 정규분포를 따른다 / 대립가설 : 오차항은 정규분포를 따르지 않는다
- 오차항이 정규분포를 따른다는 것은 오차가 평균을 중심으로 대칭적으로 분포하며, 통계적 검정의 신뢰성을 높이고, 모델의 적합성을 평가하는데 도움을 준다.
- 최종모델 Y = 1.33x - 0.05
result.predict( [0, 0.28])
# array([0.37325466])
result.params
# const -0.05
# Mean Compactness 1.33다중 회귀분석 (Multiple Regression Model)
- X가 여럿, Y를 예측
- 여기서도 회귀계수(기울기)는 최소제곱법(Ordinary Least Square)로 구함
- 다중공선성을 고려해야함 (Multi-collinearity)
- 설명변수 (X)간의 상관관계가 높아 발생하는 문제로, 설명변수간 관계가 강한 변수들에 의해 모델을 만들 때, 통제할 수 없는 오차가 발생
- 학생의 성적 A / B / C / F를 예측할 때 (Y)
- 학생의 공부시간 / 학생의 과제 제출 횟수 / 학생이 과제에 쓴 시간
- 위 변수들을 중복된 값으로 예측
- 해소방법
- 변수 선택법 / PCA 차원축소 / 등을 통해 필요한 변수만 남긴다
- 공부시간만 가지고 성적을 예측하는게 더 정확할 수 있다
- 변수 선택법 / PCA 차원축소 / 등을 통해 필요한 변수만 남긴다
- 설명변수 (X)간의 상관관계가 높아 발생하는 문제로, 설명변수간 관계가 강한 변수들에 의해 모델을 만들 때, 통제할 수 없는 오차가 발생
- 분산팽창지수 (Variation Inflation Factor : VIF)
- 다중공선성을 평가하는 지표. 높으면 다중공선성 문제가 발생할 가능성이 높음
- VIF가 1에 가까우면 다른 독립변수들과 상관관계가 낮다
- VIF가 1보다 크면 다른 독립변수들과 상관관계가 있다
- VIF가 5보다 크면 해당 독립변수가 다른 독립 변수들과 상당한 다중공선성을 가질 가능성이 있음
- 이때 변수 선택 / 변수 변환 / 정규화와 같은 방법으로 해결
- 다중공선성을 피하는 변수 선택법
- 후진제거법 : (Backward Elimination) : 모든 설명 변수 중 가장 영향력이 적은 설명변수 순으로 제거
- 전진선택법 : (Forward Selection) : 모든 변수 중 설명력이 가장 큰 변수부터 추가해나감
- 단계적 선택법 (Stepwise) : 후진제거법과 전전선택법의 단점을 보완하여 결합한 형태로 사용
- 다중공선성을 피하는 변수 선택법
- 이렇게 파악한 변수들을 모아 대표 변수만 가지고 분석/예측을 실시
# 학습할 다수의 X 변수
sel_col = [x for x in df1.columns if 'Mean' in x]
X = df1[sel_col]
Y = df1['Mean Radius'] # 예측변수
X.drop(columns = ['Mean Radius'], inplace = True) # 예측할 자기자신 제외
# 회귀모델 생성
X_const = sm.add_constant(X)
model = sm.OLS(Y, X_const)
result = model.fit()
result.summary()
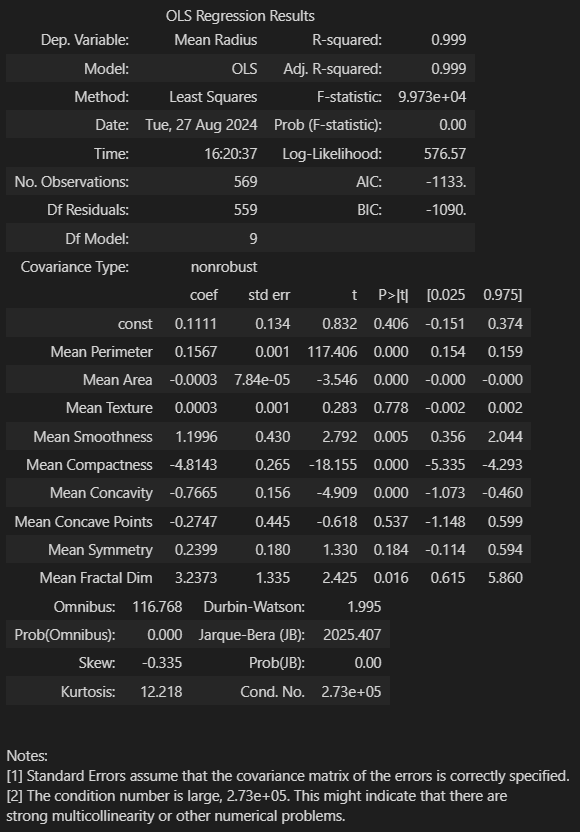
- 강한 다중공선성 문제 발생
- 이에 분산 팽창 지수 (VIF) 계산
from statsmodels.stats.outliers_influence
import variance_inflation_factor
df_VIF = pd.DataFrame()
df_VIF['variables'] = X_const.columns
# VIF 계산
df_VIF['VIF'] = [variance_inflation_factor(X_const.values, i) for i in range(X_const.shape[1])]
# X_const와 i번 컬럼의 VIF 계산
# VIF가 10이 넘어가는 (=안전한) 변수를 선택
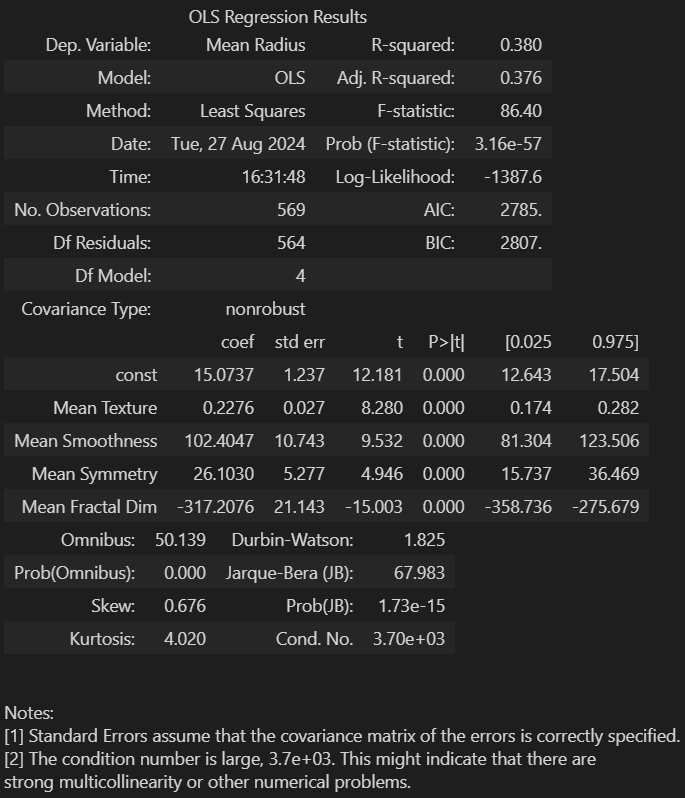
cond1 = df_VIF['VIF'] <= 10
sel_col2 = df_VIF.loc[cond1]['variables'].values
X = df1[sel_col2]
Y = df1['Mean Radius']
# 모델 재생성 / 학습
X_const = sm.add_constant(X)
model = sm.OLS(Y, X_const)
result = model.fit()
result.summary()
Analyse the world