확증적 데이터 분석 (CDA)

XTHK·2025년 3월 20일

Anaysis

목록 보기

5/23

분포 확인/검정 등

import scipy.stats as stats

확증적 데이터 분석 (Confirmatory Data Analysis)

데이터 간 연관성 상관성 유사성 등을 가설로 수립하여 객관적인 수치로 검증
통계적 가설 검정 기법을 이용해 검정을 실시
통계적 가설 검정은 확률 분포를 기반으로 실시
- 확률 분포 : 확률 변수가 어떤 값들을 가질 수 있는지, 그리고 각각의 값이 얼마나 자주 나타날 가능성이 있는지를 그래프나, 표 함수로 표현한 것
  - 예를 들면 주사위의 눈이 나올 확률 / 동전의 뒷면이 나올 확률
확률분포를 파악해야만 데이터 분포에 따른 가설검정 기법을 선택할 수 있음

확률 분포 (probability distribution)

연속형 확률 분포 / 이산형 확률 분포

1. 이산형 확률 분포

베르누이 분포 : 동시에 일어날 수 없는 두 가지 사전의 분포를 나타낸 것
- 이항분포 : 베르누이를 여러 번 시행할 때 성공한 횟수를 나타낸 분포
  - ex) 코로나 양성:음성 / 시험 합격:불합격 / 동전 앞면:뒷면
- 포아송 분포 : n : 시행 횟수 / p : 확률 / n이 매우 크고 p가 작은 매우 경우, np가 일정한 값으로 수렴한다.
  - 연속적인 시간이나, 공간에서 발생빈도가 낮은 희귀한 사건의 단위 단 발생 수 등에 적용되는 분포
pmf(probability mass function) : 확률질량함수
- 각각의 확률 변수에 대한 가능성(likelihood)이 어느 정도인지를 나타내는 함수
- 원소값 : pmf(목표값, 전체값(발생가능한 전체 건수), [확률값])

이항분포 예제 ) A사의 금일 상품 해약율이 15%나 된다고 한다. 3명의 고객을 임의로 선택했을 때, 해약고객이 각각 0, 1, 2, 3명일 확률은?

# 최대 해약고객 수
n = 3

for i in range(n+1) :
	pro = stats.binom.pmf(k=i, n=n, p=0.15)
    print(pro.round(2))
    # 0.61
	# 0.33
	# 0.06
	# 0.0

포아송분포 예제1 ) 한 은행의 고객센터에 하루 평균 5번의 스마트 뱅크 사용 VOC가 발생한다고 가정. 특정 시간 동안 VOC가 발생하지 않을 확률을 계산하시오.

voc_per_day = 5
time1 = 1 # 하루
new_voc = 0

stats.poisson.pmf(new_voc, voc_per_day * time1)
# 6%

포아송분포 예제2 ) H은행 어떤 창구에서 1시간 당 5명의 고객응대를 한다고 한다. 고객응대 횟수가 포아송 분포를 따른다면, 이 창구에서 1시간에 3명의 고객을 응대할 확률?

mean2 = 5 # 한 시간 당 5명

# 1시간에 3명 응대할 확률
stats.poisson.pmf(3, mean2 * 1)
# 14%

위와 동일한 조건에서, 1시간에 2명 이하의 고객을 응대할 확률은?

누적확률분포에서 2명 이하 응대할 확률
'3명 이상'이라면? -> 1(전체) - 2명 이하 응대할 누적확률

stats.poisson.cdf(2, mean2)
# 12%

2. 연속형 확률 분포

: 실험결과(데이터 / 사건의 결과) 연속형 값을 취하는 상황을 모형화하기 위해 사용

정규분포 : 연속형 확률변수 X가 특정 조건 하에서 무한히 많은 값으로부터 형성되는 좌우 대칭 종 모양의 분포.
- 일반적인 연속형 데이터의 분포를 나타내는 데 자주 사용. 많은 자연현상이나 실무 데이터가 정규 분포를 따르는 경향이 있다.
- 용도는 수집된 자료의 분포를 근사하는 데에 자주 사용하며, 이는 중심극한정리에 의해 독립적인 변수들의 평균이 정규분포에 가까워지는 성질 때문.
- 연속형 데이터가 외부의 변수에 의해 크게 영향을 받지 않는 상태에서 일정 개수 이상이 모였을 때, 집단 내 구성원들의 키, 몸무게, 인장강도, 온도 등 다양한 실측 데이터들이 정규분포를 따름

중심극한정리 (Central Limit Theorem)

표본의 크기가 클수록 그 표본 평균의 분포가 정규분포와 가까워진다는 점에서 중요한 통계적 성질을 가지며, 이는 표본 평균이 모평균에 대한 추정을 할 때 유용
주사위 / 동전 뒤집기의 확률은 이항분포 / 이산균등분포라는걸 따르지만, 수 없이 많이 던지는 경우, 앞면이 나오는 평균 / 주사위 합이 7이 되는 경우의 평균은 정규분포를 점점 따르게 된다.

# 정규분포 생성
np.random.seed(seed = 1234)
# seed를 선택하여 매 번 같은 랜덤 난수 생성

normal = np.random.normal(20, 2, 10000)
# 평균 20 / 표준편차 2 / 데이터를 만 개 추출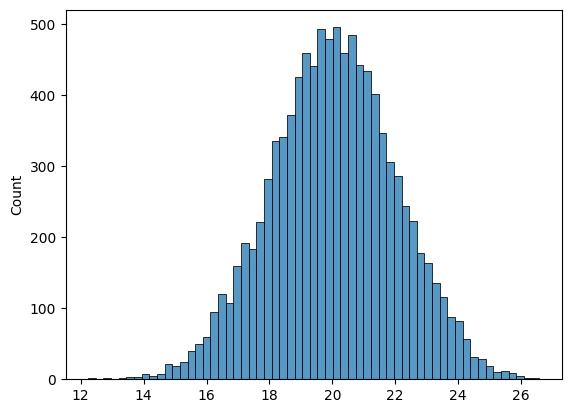

예제) 새로 출시된 어플리케이션에서 신규 고객이 계좌를 개설하는데 걸리는 시간을 측정해본 결과, 평균 16분, 표준편차 4분이 소요된다는 것을 파악했다. 해당 데이터가 정규분포를 따른다고 할 때, 신규 계좌 개설에 걸리는 시간이 20분 이상 걸리는 고객의 비율은 어느 정도인가?

데이터가 없는 상황에서 정규분포를 가정한 데이터의 추정

# 평균개설시간
mean1 = 16

# 표준편차
std1 = 4

# 알고자 하는 시간의 기준
x = 20

# 누적확률 값을 계산하여 해당 X 위치에서 데이터 비율을 알 수 있음
1 - stats.norm.cdf(x, mean1, std1)
# 15.8%

CDF : cumulative distribution function : 특정 값 이하일 때 확률을 계산 (누적분포함수)

표준정규분포 (standard normal distribution)

평균이 0, 표준편차가 1인 정규분포
모든 정규분포를 같은 기준으로 비교하기 위해 만든 틀

T분포 (T distribution)

정규 분포의 평균을 측정하기 위해 고안된 분포로, 정규 분포와 유사하지만, 표본 크기에 따라 분포의 꼬리가 조금 더 두꺼운 모습을 하고 있는 분포
예상하는 값과 같은지를 검정
꼬리가 두껍다는건, 평균에서 멀리 떨어진 극단적인 값이 더 자주 발생한다는 말
정규분포와 유사하지만, 표본 수가 더 작거나, 변동성이 더 클 때 사용

카이제곱 분포 (Chi² Square Distribution)

정규분포에서 유도된다 : 여러 독립적인 정규분포 변수의 제곱합으로부터 유도
정규분포가 데이터의 개별적인 분포를 설명한다면,
카이제곱 분포는 데이터 분석 결과를 검정하는데 쓴다
적합도 검정 : 관찰된 데이터가 특정 이론적 모델 (예:정규분포)를 잘 따르는지 검정합니다
- 예상하는 값과 얼마나 유사한지 보기 위해 사용
독립성 검정 : 두 범주형 변수 간의 관계를 검정합니다 :
- 두 변수가 독립인지 아닌지를 검정할 때 사용

F분포 (F distribution)

실제로 다르다는 것을 검정하기 위해 사용
변동성 평가 : F분포는 두 개 이상의 집단 간의 분산 차이를 비교하는 데 사용
- 집단 간 변동성과, 집단 내 변동성을 평가하여 실제로 유의미한 차이가 있는지 검정
ANOVA 테스트 할 때 F분포를 사용한다
- 회귀 모형 자체의 유의성 검정에 F분포를 사용
- 회귀모형이 전체적으로 통계적으로 유의미한지, 즉 독립 변수들이 종속 변수를 설명하는데 충분한지 평가하는 데는 F 검정을 사용

와이블 분포 (Weibull Distribution)

와이블 분포는 생존 시간 / 실패 시간 같은 지속적인 데이터의 분포를 모델링하는 데 사용됨
어떤 전구는 오래가고 어떤 전구는 수명일 짧을 때, 와이블 분포는 이 차이를 설명해준다
제조 : 부품 수명 / 신뢰성 공학 : 실패 분석 / 제조에 걸리는 시간
금융 : 신용 리스크 모델링 / 수익률 평가 / 파산 예측

from scipy.stats import weibull_min

와이블분포 예제 ) 어떤 전자제품의 수명이 와이블 분포를 따르며, 형태 모수 k 가 1.5, 척도 모수 lambda가 5000인 것으로 알려져 있다. 이 전자제품이 4000시간 이내에 고장 날 확률은 얼마인가?

k = 1.5
lambda_ = 5000
time1 = 4000 # 목표변수

prob = weibull_min.cdf(time1, k, scale = lambda_)

형태 모수(k) : 와이블 분포 곡선의 모양을 결정
- k < 1 : 분포가 오른쪽으로 치우치며, 시간이 감에 따라 고장률이 감소
- k = 1 : 와이블 분포는 지수 분포와 같아지며, 시간에 관계 없이 일정한 고장률을 가짐
- k > 1: 분포가 왼쪽으로 치우치며, 시간이 지남에 따라 고장률이 증가
척도 모수 lambda : 와이블 분포의 스케일(크기)을 조정하는 역할

추론 통계 (Inferencial Statistics)

기술 통계 : 수집된 데이터의 평균, 분산 등의 요약 통계량을 계산해 해당 데이터의 직접적 특성을 파악
추론 통계 : 표본에 포함된 정보로부터 모집단의 특성을 파악하고 타당성을 검토하며 모수를 추론하거나 미래를 예측
- 추론 통계 활용:
  - 통계적 추정 (statistical estimation) : 표본의 성격을 나타내는 통계량을 기초로 모수를 추정
  - 가설검정 (hypothesis test) : 모수에 대한 특정한 가설을 세워놓고, 표본을 선택하여 통계량을 계산한 다음, 이를 기초로 모수에 대한 가설의 진위를 판단
- 이론적 매커니즘 :
  - 모수 (parameter) : 모집단 (population)에서 나온 수치 (모평균/모분산/..)
  - 통계량 (statistic) : 표본 (sample)에서 나온 수치 (평균 / 분산 / ..)
  - 표본과 모집은 같지 않으므로, 표본으로 구해지는 결론과 추정치들은 항상 옳지는 않다
  - 그래서 통계적 추론에 신뢰의 척도, 즉 신뢰수준 (confidence level)과 유의수준 (significant level)이 필요
- 신뢰구간 (confidence interval) : 특정 표본에서 모수를 포함할 수 있는 구간이다
  - 1 - a 를 신뢰 수준이라고 한다 (95%)
  - a : 유의수준 (significant level alpha) : 잘못된 결론을 내릴 확률 (5%)
  - 신뢰수준은 여러 번 표본을 추출해 신뢰구간을 계산했을 때, 그 구간들이 모수를 포함할 비율을 의미

통계적 가설 검정

특정한 주장을 가설로 수립한 후, 이 가설이 주어진 데이터에 비추어 참인지 거짓인지를 통계적 방법을 사용해 판단하는 과정
귀무가설 : 기각시킬 목적으로 수립하는 가설 (대립가설의 반대)
- 현재까지 주장되어온 것이거나 변화에 차이가 없음을 설명하는 가설
- 일반적으로 알려져 있는 사실을 귀무가설로 설정
- 통계적 관점에서 일반적인 상황:
  - 수집된 표본은 서로 독립적이다
  - 위의 가정을 바탕으로, 집단 간 평균이 같다 / 두 데이터가 서로 연관성이 없다 / 두 항목이 서로 독립이다를 이야기할 수 있다
  - 정규분포를 가정하는 방법이 자주 사용된다 (t검정 / anova / 회귀분석)
대립가설 : 주장하려는 바, 샘플로부터 근거를 통해 '증명하고자 하는 가설'
귀무가설이 기각될 때, 대립가설을 채택
집단 간 평균이 다르다 / 두 데이터가 서로 연관성이 있다 / 두 항목이 독립이 아니다 / 정규분포를 따르지 않는다
가설검정의 근간 :
1. 수집된 데이터는 서로 독립적으로 수집되었다
2. 표본은 하나의 모집단에서 추출된 것이다
3. 두 개의 표본은 독립적일 때, 하나의 모집단에서 추출된 것이다

a - risk / b - risk

실제 가설 검정 수행 시, 가설검정의 결과가 실제 벌어지는 현상과 다른 경우가 있음
이유는 가설검정이 현재 수집된 데이터를 표본으로 가정하고, 모집단을 추정해 참인지 거짓인지 결론을 내리는 것이기 때문
그래서 가설 검정에는 2가지 risk가 존재
- a-risk (1종오류) : 귀무가설이 참인데, 대립가설을 선택
- b-risk (2종오류) : 대립가설이 참인데, 귀무가설을 선택
검정력 (power of the test) : 귀무가설이 틀렸을 때, 대립가설을 채택할 확률을 의미
유의 수준 (a = 5 / 5%) : 가설검정의 판단 기준치
- 귀무가설 H0이 참일 때, 귀무가설을 기각할 오류를 범할 확률의 최대 허용한계
  - P-value > 5% : 귀무가설을 채택
  - P-value < 5% : 대립가설을 채택
Ex) 10대와 20대의 주당방문횟수의 평균에는 차이가 있는가?
- 귀무가설 : 10대와 20대의 주당방문횟수의 평균에는 차이가 없다
- 대립가설 : 10대와 20대의 주당방문횟수의 평균에는 차이가 있다
- p value가 3% 라면, 대립가설을 채택한다.
- 10대와 20대의 주당방문횟수의 평균은 통계적으로 유의미하게 차이가 있다

단일변수 검정

정규성 검정
- 귀무가설 : age는 정규분포를 따를 것이다
- 대립가설 : age는 정규분포를 따르지 않을 것이다
- na값이 있으면 na로 나오므로 결측값 처리 (fillna)

stats.normaltest(df1['Age'].fillna(df1['Age'].mean()))
# p-value : 0.0 -> 대립가설 채택

1표본 평균 검정
- 하나의 집단의 평균과 단일값이 같은지 다른지 테스트
- ttest_1samp

df1['Age'].mean()

1표본 평균 검정 예제 ) 2023년도 목표 평균 월렌탈비용이 10만원이라고 할 때, 해당 월렌탈비용의 평균은 10만원과 같다고 볼 수 있는가?

T-Test
정규성 검사 선행 후 1표본 평균 검정 수행 (정규성을 따른다면)
귀무가설 : 23년도 월렌탈비용의 평균은 10만원과 같다
대립가설 : 23년도 월렌탈비용의 평균은 10만원과 다르다

stats.ttest_1samp(p1['Amount_Month'], 100000)
# pvalue = 2.913974690307771e-302
# 대립가설 채택

정규성을 따르지 않는다면

import statsmodel.stats.descriptivestats as statsd

statsd.sign_test(p1['Amount_Month'],100000)

다변수 검정

X 범주형 Y 연속형 : 집단 간 통계량 비교
X 연속형 Y 연속형 : 집단, 두 숫자 데이터의 상관성 비교
X 범주형 Y 범주형 : 두 범주 데이터의 독립성 비교

X 범주형 Y 연속형

두 집단의 비교
- 모두 정규분포를 따른다면
  - 등분산검정 (bartlett) -> 5% 이상이라면
    - ttest_ind
- 둘 중 하나라도 정규분포를 따르지 않는다면 : ranksums
세 집단의 비교
- 모두 정규분포를 따른다면
  - 등분산검정 (bartlett) -> 5% 이상이라면
    - 평균비교 (f_oneway)

예제 ) 렌탈 계약 고객과 멤버십 계약 고객의 월렌탈 비용은 통계적으로 유의미한 차이가 있는가?

귀무가설 : 렌탈 고객과 멤버십 고객의 월렌탈비용에는 차이가 없을 것이다
대립가설 : 차이가 있을 것이다

cond1 = df1['Sales_Type'] == '렌탈'

rental = df1.loc[cond1]
member = df1.loc[~cond1]

# 정규성 검정
stats.normaltest(rental['Amount_Month']) # pvalue=0.0
stats.normaltest(member['Amount_Month']) # pvalue=3.6389427819364256e-123
# 두 고객의 월렌탈 비용 모두 정규성을 따르지 않음
# 둘 중 하나라도 따르지 않으면 ranksums

stats.ranksums(rental['Amount_Month'], member['Amount_Month'])
# pvalue=0.0 -> 대립가설 채택

예제2 ) 3집단 비교 : 평균 월렌탈비용이 높은 상위 3개 채널을 비교하려고 한다.

# 정규성 검정 후, 세 집단 중 하나라도 정규분포를 따르지 않는다면

stats.kruskal(t1['Amount_Month'], t2['Amount_Month'], t3['Amount_Month'])
# pvalue=1.1990045357893553e-05
# 3집단이 모두 통계적으로 유의미하게 다르다

X 연속형 Y 연속형

시각화 방법
- px.scatter : 원형을 띄면 상관성이 매우 약한 것
- trendline = 'ols'로 회귀선 추가 (기울기가 0이면 상관성 x)
정규분포 검정 -> 두 집단 모두 따른다면
- pearsonr 검정
정규분포를 따르지 않는다면
- spearmanr 검정

X 범주형 Y 범주형

chi2_contigency() 검정
- crosstab로 사전 처리 후 검정

XTHK

Analyse the world

이전 포스트

정규표현식 (Regular Expression)

다음 포스트

확증적 데이터 분석 (CDA)

Anaysis

확증적 데이터 분석 (Confirmatory Data Analysis)

확률 분포 (probability distribution)

1. 이산형 확률 분포

이항분포 예제 ) A사의 금일 상품 해약율이 15%나 된다고 한다. 3명의 고객을 임의로 선택했을 때, 해약고객이 각각 0, 1, 2, 3명일 확률은?

포아송분포 예제1 ) 한 은행의 고객센터에 하루 평균 5번의 스마트 뱅크 사용 VOC가 발생한다고 가정. 특정 시간 동안 VOC가 발생하지 않을 확률을 계산하시오.

포아송분포 예제2 ) H은행 어떤 창구에서 1시간 당 5명의 고객응대를 한다고 한다. 고객응대 횟수가 포아송 분포를 따른다면, 이 창구에서 1시간에 3명의 고객을 응대할 확률?

위와 동일한 조건에서, 1시간에 2명 이하의 고객을 응대할 확률은?

2. 연속형 확률 분포

중심극한정리 (Central Limit Theorem)

표준정규분포 (standard normal distribution)

T분포 (T distribution)

카이제곱 분포 (Chi² Square Distribution)

F분포 (F distribution)

와이블 분포 (Weibull Distribution)

와이블분포 예제 ) 어떤 전자제품의 수명이 와이블 분포를 따르며, 형태 모수 k 가 1.5, 척도 모수 lambda가 5000인 것으로 알려져 있다. 이 전자제품이 4000시간 이내에 고장 날 확률은 얼마인가?

추론 통계 (Inferencial Statistics)

통계적 가설 검정

a - risk / b - risk

단일변수 검정

1표본 평균 검정 예제 ) 2023년도 목표 평균 월렌탈비용이 10만원이라고 할 때, 해당 월렌탈비용의 평균은 10만원과 같다고 볼 수 있는가?

다변수 검정

예제 ) 렌탈 계약 고객과 멤버십 계약 고객의 월렌탈 비용은 통계적으로 유의미한 차이가 있는가?

예제2 ) 3집단 비교 : 평균 월렌탈비용이 높은 상위 3개 채널을 비교하려고 한다.

정규표현식 (Regular Expression)

결측치 처리

0개의 댓글