오늘 뭘 했니?

1. 캐글 집값예측 데이터에 피쳐엔지니어링에 대한 기초개념 적용
   실습파일: 0707-house-prices-feature_engineering-input.ipynb

2.0708-house-feature_engineering-predict-input

뭘 배웠니?(new)

변수 스케일링과 트랜스포메이션

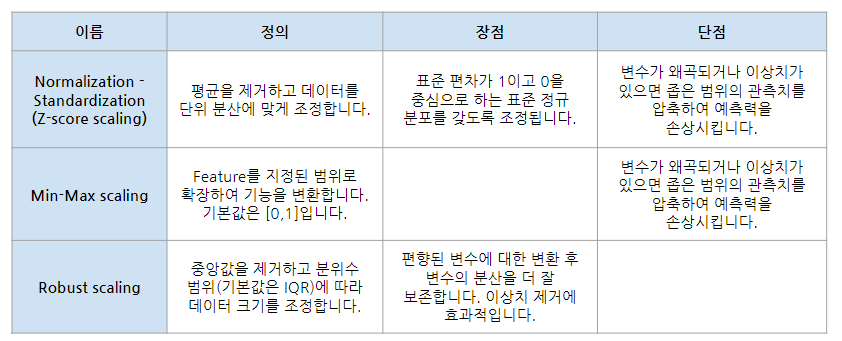
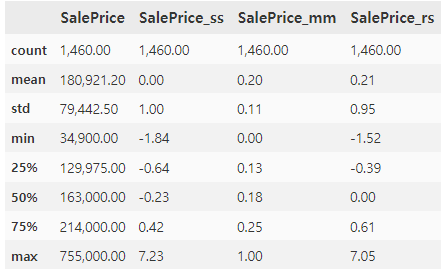
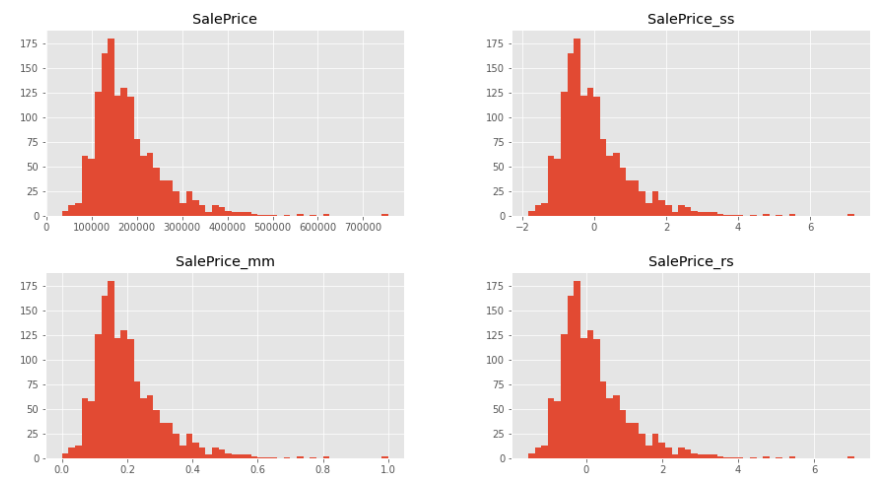
• 트리 모델에서는 스케일러가 큰 성능 X
• 다른 알고리즘에서는 대체적으로 머신러닝 알고리즘이 해석하는데 도움이 됨

Standard Scaler

• 평균이 0, 표준편차가 1
• Z-score scaling
• z = (X - X.mean) / std

MinMax Scaler

• 최소값이 0, 최대값이 1
• X_scaled = (X - X.min) / (X.max - X.min)

Robust Scaler

• 는 IQR을 기준으로 scaling 하기 때문에 Standard Scaler보다 더 큰 최소값, 더 작은 최대값을 갖게 됨
• median 값이 0이므로 데이터의 절반은 양수, 절반은 음수로 생각할 수 있다.
• X_scaled = (X - X.median) / IQR
• 이상치에 대해 비교적 강점이 있음

트랜스포메이션 Log Transformation (log1p)

• 음수값에 로그를 취하려면 체값의 최소값의 절대값만큼 평행이동 시킨다음에 최솟값 +1 을 더한후에 로그 ㄱㄱ
• Feature Scaling을 했어도아직 표준정규분포 형태가 아님
• log transformation → 좀 더 정규분포 형태에 가까워짐
• Log Transformation을 적용하는 이유는 log 함수가 x값에 대해 상대적으로 작은 스케일에서는 키우고, 큰 스케일에서는 줄여주는 효과가 있기 때문
  

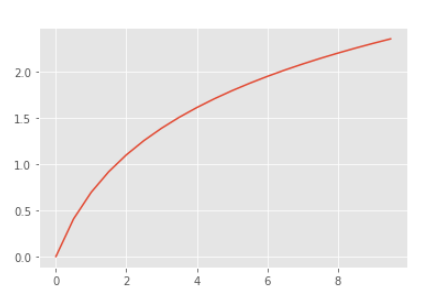
• log 함수는 x값이 커질수록 기울기가 완만해짐
• x값이 작을수록 y의 변화량이 크고, x값이 클수록 y의 변화량이 작다는 뜻
• 작은 숫자들 사이의 차이는 벌어지고, 큰 숫자들 사이의 차이는 줄어듦

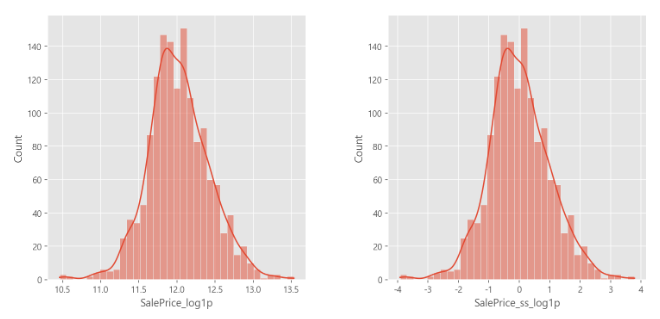
• log transformation만 적용해도 정규분포 형태
• 여기에 Standard Scaler를 적용하면 표준 편차가 1이고 0을 중심으로 하는 표준정규분포 완성!
  

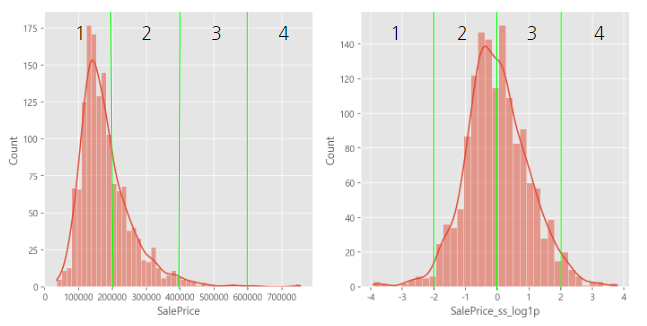
• 이미 잘 분포되어 있는 Feature의 경우에는 Transformation이 불필요할수도 있지만 편향된 Feature에 log적용하면 y값을 예측하는 데 더 유용
• 분포가 완만해져서 학습에 유리함
• 1,4 분위보다 2,3분위가 예측 성능이 더 좋을 확률

💡 예측하려는 Feature가 편향되어 있다면 ?

• label을 transformation해서 예측한 다음, 예측 값에 np.exp() 적용하여 출력
• log 함수는 지수함수와 역함수 관계이기 때문에 np.exp()를 이용하면 둘 사이의 변환이 간편

• log 함수는 x가 0으로 수렴할 때, y가 -∞로 발산하므로 +1 해서 로그변환해주는건이 안전함
• np.log1p
• np.exp1m

fit / transform / fit_transform

• one-hot인코딩처럼 생각하자

fit & transform 과 fit_transform의 차이가 무엇인가요? - 인프런 | 질문 & 답변 (inflearn.com)

이산화

• 이산화(Discretisation)는 Numerical Feature를 일정 기준으로 나누어 그룹화하는 것 (수치 →범주)

1. cut
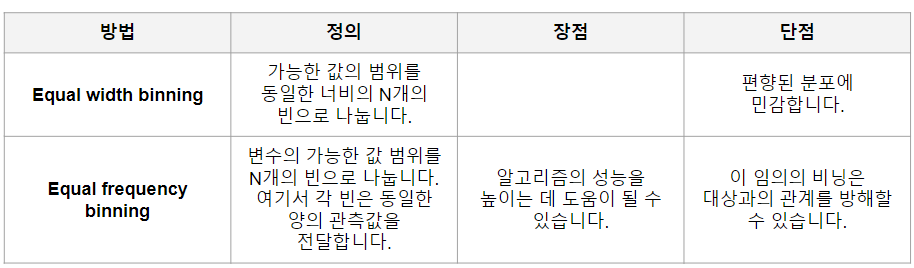
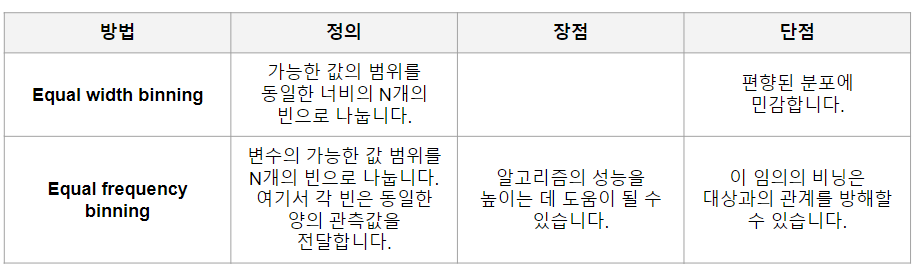
   범위를 기준으로 나누는 것(Equal width binning)
   한 분할 안에 몇개가 들어가는지와 무관하게 n분할 ex) 절대평가
2. qcut
   빈도를 기준으로 나누는 것(Equal frequency binning)
   개수를 기준으로 n분할 ex) 상대평가

인코딩

• Categorical Feature를 Numerical Feature로 변환하는 과정 (범주 → 수치)
• 데이터 시각화와 머신러닝 모델에 유리함
  • 변화의 추이를 관찰(lineplot)하거나, 산점도(scatterplot)를 그려 관찰하고 싶을 경우
  • 선형회귀 모델, 딥러닝 모델 등 Categorical Feature를 이용할 수 없는 모델을 사용하는 경우

오디널 인코딩(Ordinal-Encoding)

• 직관적이다
• 순서가 있어서 비교하기가 쉽다
• 컬럼을 하나만 만들어돼서 메모리 절약
• 단점: 순서에 의미가 생길 수도 있음
• pandas에서는 Ordinal-Encoding을 category 타입에 대해서 cat 속성의 codes 속성으로 지원
• sklearn에서는 Ordinal-Encoding을 OrdinalEncoder 객체로 지원

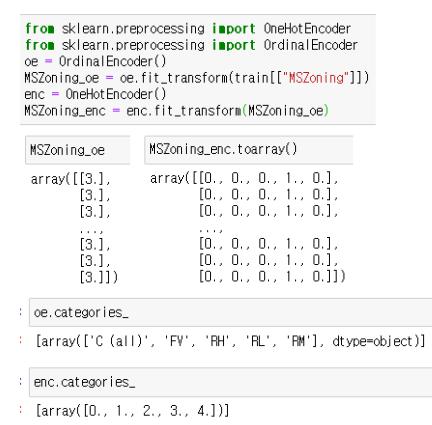
원핫인코딩

• One-Hot-Encoding은 Categorical Feature를 다른 bool 변수(0 또는 1)로 대체하여 해당 관찰에 대해 특정 레이블이 참인지 여부
• 단점: 희소행렬이 생겨 메모리를 너무 많이 차지할 수도 있음 (→ 차원축소 알고리즘으로 극뽁)
• pandas에서는 One-Hot-Encoding을 get_dummies 메서드로 지원
• sklearn에서는 One-Hot-Encoding을 OneHotEncoder 객체로 지원

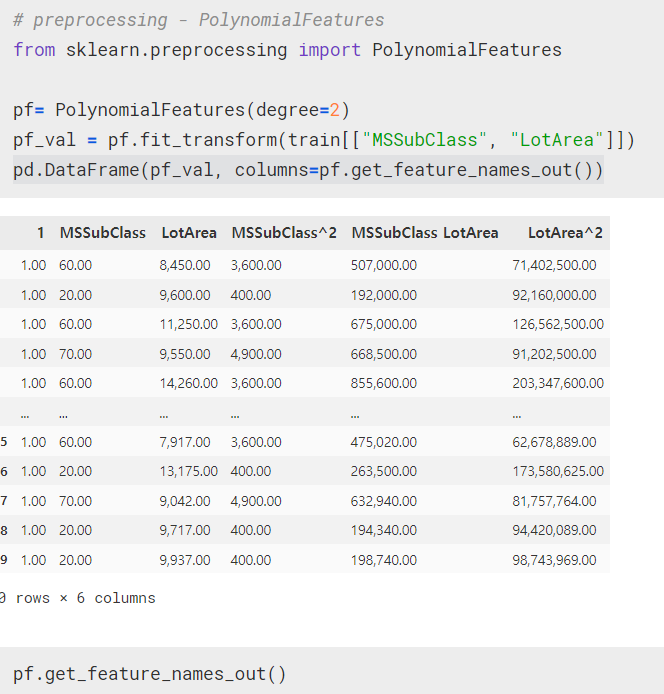
다항식전개에 기반한 파생변수 생성

• sklearn 라이브러리에서는 PolynomialFeatures 객체를 통해 다항식 전개에 기반한 파생변수 생성을 지원
• 머신러닝 모델은 label에 대해서 설명력이 높은 한 두가지 Feature에 의지할 때보다 여러가지 Feature에 기반할 때 성능이 더 뛰어나기 때문
• 다항식 전개에 기반해서 파생변수를 만들게 되면 머신러닝 모델이 여러 Feature에 기반하게 되어 안정성이 높아짐
• degree 파라미터는 다항식의 최대 차수를 지정

Feature Selection 변수선택

분산 기반(Variance Based) Feature Selection

• Feature가 대부분 같은 값으로 이루어져 있거나 모두 다른 값으로 이루어져 있다면, 예측에 도움 안됨( 상황에 따라 특정 Feature가 변동성이 낮다는 것도 중요한 정보가 될 수 있긴 함)

상관관계 기반(Correlation Based) Feature Selection

• 어떤 Feature들은 지나치게 높은 상관관계를 가지고 있어서 하나만 채택하더라도 무관
• 이런 경우에는 머신러닝 모델의 과적합을 막거나 학습 시간을 줄이기 위해서 하나만 채택 가넝

왜도와 첨도

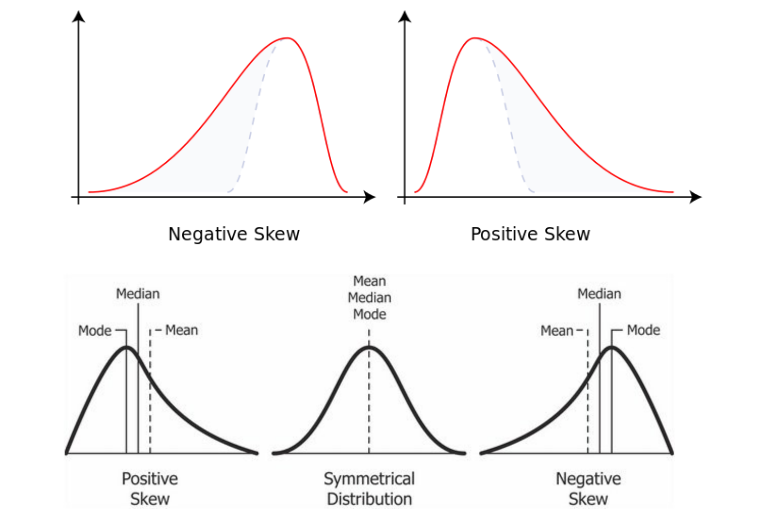
왜도

• 실수 값 확률 변수의 확률 분포 비대칭성을 나타내는 지표
• 왜도의 값은 양수나 음수가 될 수 있으며 정의되지 않을 수도 있다.
• 왜도가 음수일 경우에는 확률밀도함수의 왼쪽 부분에 긴 꼬리를 가지며 중앙값을 포함한 자료가 오른쪽에 더 많이 분포해 있다.
• 왜도가 양수일 때는 확률밀도함수의 오른쪽 부분에 긴 꼬리를 가지며 자료가 왼쪽에 더 많이 분포해 있다는 것을 나타낸다.
• 평균과 중앙값이 같으면 왜도는 0이 된다.

첨도

• 확률분포의 뾰족한 정도를 나타내는 척도
• 관측치들이 어느 정도 집중적으로 중심에 몰려 있는가를 측정할 때 사용
• 첨도값(K)이 3에 가까우면 산포도가 정규분포에 가깝다.
• 3보다 작을 경우에는(K<3) 정규분포보다 더 완만하게 납작한 분포로 판단할 수 있으며,
• 첨도값이 3보다 큰 양수이면(K>3) 산포는 정규분포보다 더 뾰족한 분포로 생각할 수 있다.
  

print("왜도(Skewness):", train["SalePrice"].skew())
print("첨도(Kurtosis):", train["SalePrice"].kurtosis())

기타

• plt.subplots(행,컬럼)

fig, axes = plt.subplots(1,2)
sns.countplot(data = train, x=train["SalePrice_cut"], ax=axes[0])
sns.countplot(data= train, x=train["SalePrice_qcut"], ax=axes[1])

• 소수점 둘째짜리까지만 보이게 변경
  pd.options.display.float_format = '{:,.2f}'.format

train.select_dtypes(include="number").info()

• heatmap mask

corr = train.corr()
mask = np.triu(np.ones_like(corr))

plt.figure(figsize=(25,12))
sns.heatmap(data=corr, annot=True, cmap="coolwarm", fmt=".2", mask=mask)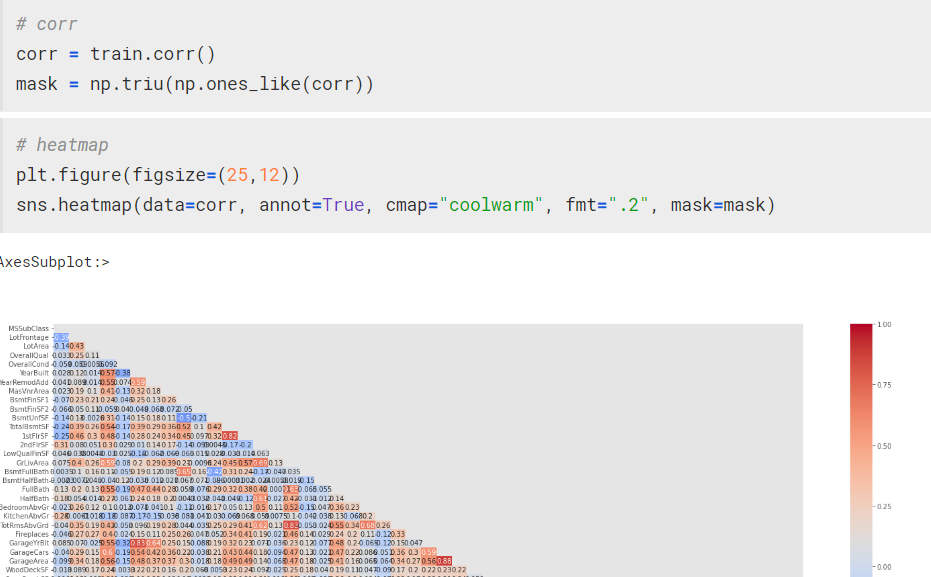

• set으로 train test 컬럼 비교

# set을 활용해서 컬럼을 비교합니다.
set(train.columns.tolist())-set(test.columns.tolist())

부족한 것

fig axes 로 받는다는게 머선말이노

fig, axes = plt.subplots(1,2)

fig, axes = plt.subplots(1,2, figsize=(12,3))
sns.countplot(data = train, x=train["SalePrice_cut"], ax=axes[0])
sns.countplot(data= train, x=train["SalePrice_qcut"], ax=axes[1])

displot이 머더라

# SalePrice 의 displot
sns.displot(data=train, x="SalePrice")

3F

사실(Fact) : 스케일러와 피쳐엔지니어링에 대해 배웠다.
느낌(Feeling) : 조금씩 알 거같으면서도 막상 혼자하라고하면 못할듯..
교훈(Finding) : 체력분배를 잘하자