이번 문제는 다이나믹 프로그래밍을 통해 해결하였다. 점화식을 찾는 과정이 어려웠는데 다른 사람의 풀이를 어느정도 참고하여 2가지의 점화식을 도출해냈다. 점화식을 도출하기 위해 다음과 같이 도식화하였다.


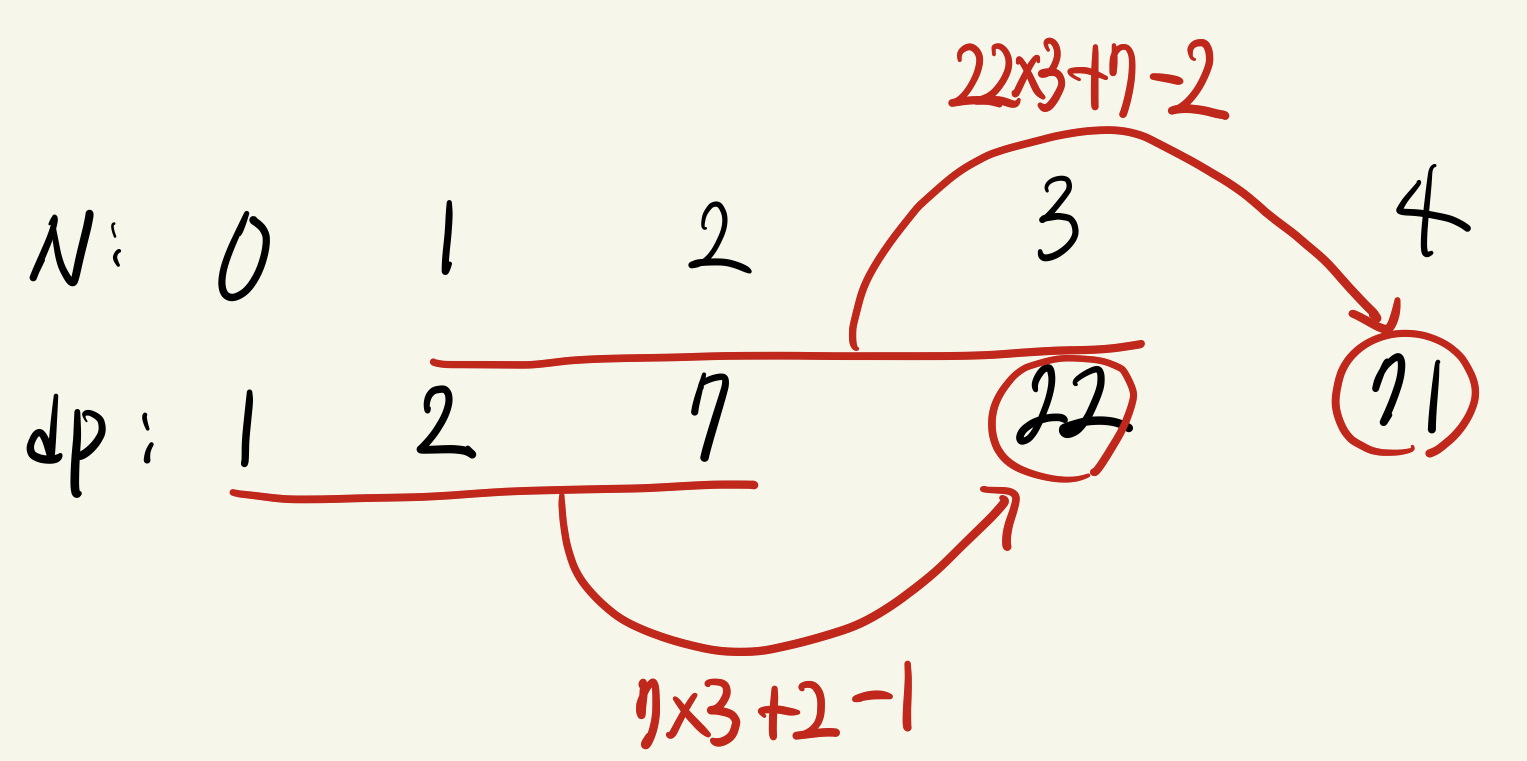
첫번째 점화식은 dp[i-3], dp[i-2], dp[i-1]을 사용하여 구하는 방식으로 다음과 같이 표현할 수 있다.
dp[i]=dp[i-1]*3+dp[i-2]-dp[i-1]
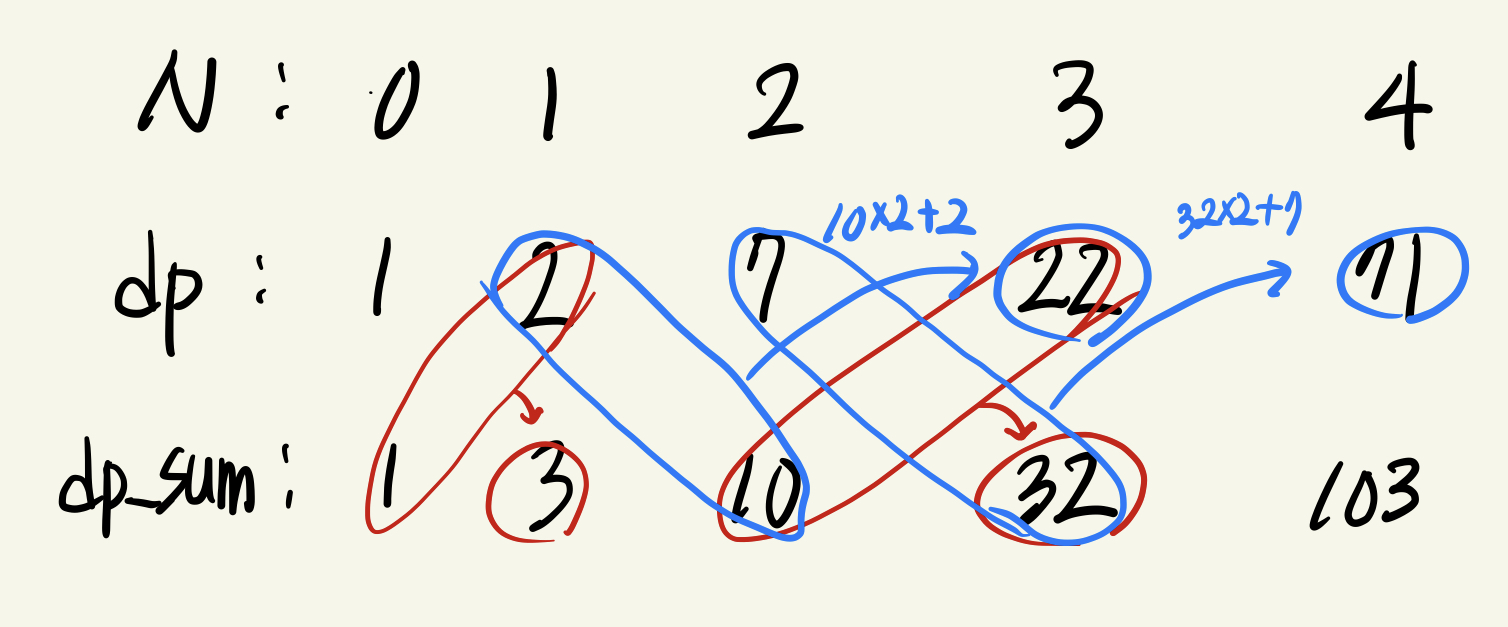
두번째 점화식은 dp[i-2], dp[i-1], 그리고 이전까지의 dp의 누적합을 이용하여 구하는 방식으로 다음과 같이 표현할 수 있다.
dp[i]=dp_sum[i-1]*2+dp[i-2]
dp_sum[i]=dp_sum[i-1]+dp[i]

첫번째 점화식 풀이

• n을 입력받는다.
• dp를 n+2의 크기로 선언하고 0으로 채운다. (dp[2]까지 초기에 선언되어야 하므로 n+2로 선언해야 한다.)
• dp[0]을 1로 갱신한다.
• dp[1]을 2로 갱신한다.
• dp[2]를 7로 갱신한다.
• 만약 n이 2 이하일 경우, dp[n]을 출력하고 프로그램을 종료한다.
• 3부터 n까지 반복하는 i에 대한 for문을 돌린다.
  -> dp[i]를 (dp[i-1]*3+dp[i-2]-dp[i-3])%1000000007 으로 갱신한다.
• dp[n]%1000000007을 출력한다.

두번째 점화식 풀이

• n을 입력받는다.
• dp를 n+1의 크기로 선언하고 0으로 채운다.
• dp_sum을 n+1의 크기로 선언하고 0으로 채운다.
• dp[0], dp[1]을 1, 2로 선언한다.
• dp_sum[0]을 1로 갱신한다.
• dp_sum[1]을 dp_sum[0]+dp[1]로 갱신한다.
• 만약 n이 1 이하일 경우, dp[n]을 출력하고 프로그램을 종료한다.
• 2부터 n까지 반복하는 i에 대한 for문을 돌린다.
  -> dp[i]를 (dp_sum[i-1]*2+dp[i-2])%1000000007 으로 갱신한다.
  -> dp_sum[i]를 (dp_sum[i-1]+dp[i])%1000000007 으로 갱신한다.
• dp[n]%1000000007을 출력한다.

Code

첫번째 점화식 풀이이다.

n=int(input())
dp=[0 for _ in range(n+2)]
dp[0]=1
dp[1]=2
dp[2]=7
if n<=2:
    print(dp[n])
    quit()
for i in range(3, n+1):
    dp[i]=(dp[i-1]*3+dp[i-2]-dp[i-3])%1000000007
print(dp[n]%1000000007)

두번째 점화식 풀이이다.

n=int(input())
dp=[0 for _ in range(n+1)]
dp_sum=[0 for _ in range(n+1)]
dp[0], dp[1]=1, 2
dp_sum[0]=1
dp_sum[1]=dp_sum[0]+dp[1]
if n<=1:
    print(dp[n])
    quit()
for i in range(2, n+1):
    dp[i]=(dp_sum[i-1]*2+dp[i-2])%1000000007
    dp_sum[i]=(dp_sum[i-1]+dp[i])%1000000007
print(dp[n]%1000000007)

두번째 점화식이 누적합 리스트를 함께 이용하여 메모리 사용이 더 많은 것을 확인할 수 있었다.