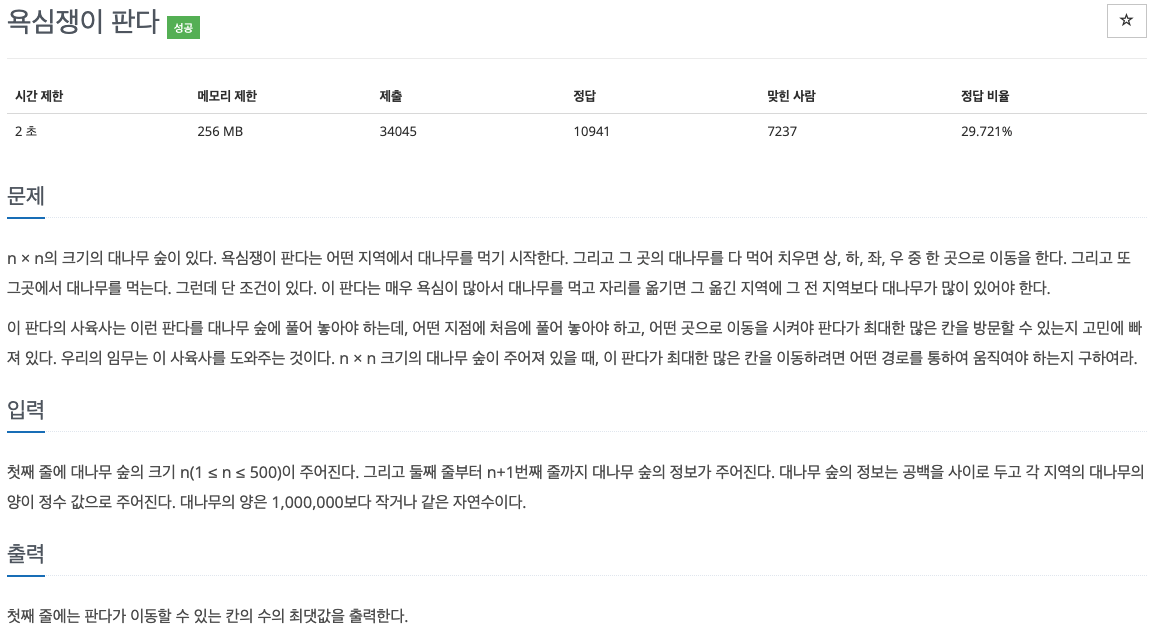
이번 문제는 다이나믹 프로그래밍을 통해 해결하였다. DFS를 통해 탐색해가며 dp리스트에 메모라이제이션한 값을 이용하였다.

처음에는 dp[i][j]에 (i, j)가 최대 몇번째 방문 대나무인지에 대한 값을 저장하도록 하였다. 그러나 이 방법은 시간초과가 발생하였다. 다른 풀이에 대해 생각하였고, (i, j)에서 가장 많이 갈 수 있는 대나무의 수를 dp[i][j]에 저장하기로 하였다. 이 방식으로 접근하자 시간초과가 발생하지 않았고, 해결할 수 있었다.

Code

처음 코드 (시간초과)

import sys
sys.setrecursionlimit(10**6)
n = int(input())
bamboo = [list(map(int, input().split())) for _ in range(n)]
dp = [[1 for _ in range(n)] for _ in range(n)]
dy, dx = [0, 1, 0, -1], [1, 0, -1, 0]
def find_max(y, x):
    for i in range(4):
        ny, nx = y+dy[i], x+dx[i]
        if 0 <= ny < n and 0 <= nx < n:
            if bamboo[ny][nx] > bamboo[y][x] and dp[ny][nx] < dp[y][x]+1:
                dp[ny][nx] = dp[y][x]+1
                find_max(ny, nx)
for i in range(n):
    for j in range(n):
        if dp[i][j] == 1:
            find_max(i, j)
answer = 0
for i in range(n):
    answer = max(answer, max(dp[i]))
print(answer)

정답 코드

import sys
sys.setrecursionlimit(10**6)
n = int(input())
bamboo = [list(map(int, input().split())) for _ in range(n)]
dp = [[-1 for _ in range(n)] for _ in range(n)]
dy, dx = [0, 1, 0, -1], [1, 0, -1, 0]
def find_max(y, x):
    if dp[y][x] == -1:
        dp[y][x] += 1
        for i in range(4):
            ny, nx = y+dy[i], x+dx[i]
            if 0 <= ny < n and 0 <= nx < n and bamboo[ny][nx] > bamboo[y][x]:
                dp[y][x] = max(dp[y][x], find_max(ny, nx))
    return dp[y][x]+1
answer = 0
for i in range(n):
    for j in range(n):
        answer = max(answer, find_max(i, j))
print(answer)