이번 문제는 다이나믹 프로그래밍을 통해 해결하였다. 우선 점화식을 구하기 위해 도식화해보았다.

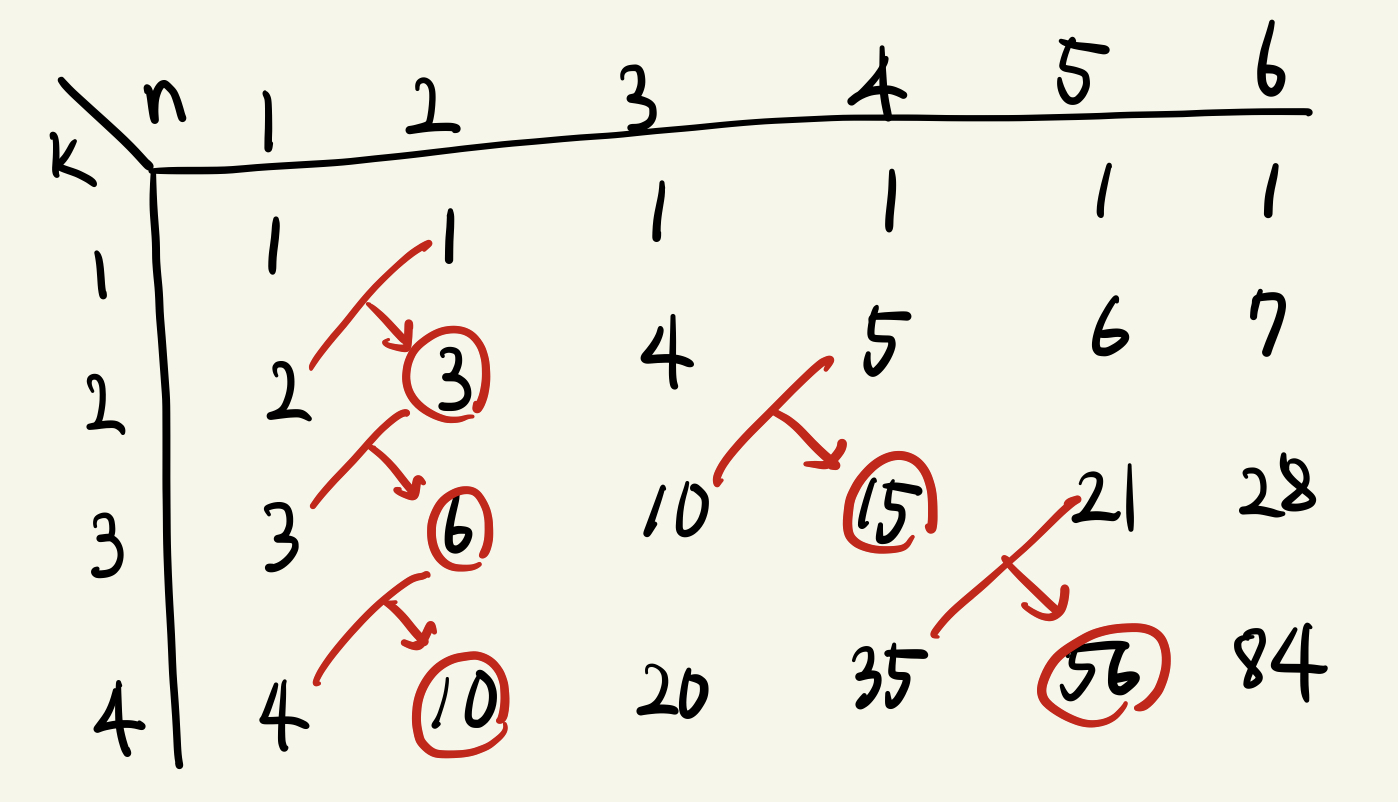
k가 1일 때의 dp는 모두 1로 채워지고, n이 1일 때의 dp는 모두 k로 채워진다. 그리고 dp[i][j]는 dp[i][j-1]+dp[i-1][j]의 값으로 갱신되는 것을 볼 수 있다. 따라서 점화식은 다음과 같이 정의할 수 있다.
dp[i][j]=dp[i][j-1]+dp[i-1][j]
이 점화식을 이용하여 코드를 작성하였다.

• n, k를 입력받는다.
• dp를 (k+1)*(n+1)의 리스트로 선언하고 0으로 채운다.
• 1부터 n까지 반복하는 i에 대한 for문을 돌린다.
  -> dp[1][i]를 1로 갱신한다.
• 1부터 k까지 반복하는 i에 대한 for문을 돌린다.
  -> dp[i][1]을 i로 갱신한다.
• 2부터 k까지 반복하는 i에 대한 for문을 돌린다.
  -> 2부터 n까지 반복하는 j에 대한 for문을 돌린다.
  --> dp[i][j]를 (dp[i][j-1]+dp[i-1][j])%1000000000로 갱신한다.
• dp[k][n]%1000000000을 출력한다.

Code

n, k=map(int, input().split())
dp=[[0]*(n+1) for _ in range(k+1)]
for i in range(1, n+1):
    dp[1][i]=1
for i in range(1, k+1):
    dp[i][1]=i
for i in range(2, k+1):
    for j in range(2, n+1):
        dp[i][j]=(dp[i][j-1]+dp[i-1][j])%1000000000
print(dp[k][n]%1000000000)