이번 문제는 DP를 통해 해결하였다. 수열은 1 -> 01 -> 1001 -> 01101001 -> 1001011001101001 -> ... 으로 구성된다. 이때 만들어진 문자열들을 반으로 잘라 보면 다음과 같은 규칙을 찾을 수 있다.
n 2 3 4 5
[:len//2] 0 10 0110 10010110
[len//2:] 1 01 1001 01101001앞쪽과 뒷쪽이 XOR연산을 했을 때 모두 1로 변환되는 것을 볼 수 있다. 이를 통해서 n-1번째 문자열의 절반 앞쪽을 A, 절반 뒷쪽을 B라고 했을 때 n번째 문자열은 BAAB의 형태가 된다. 이를 이용하여 점화식을 구하기 위해 결과값들을 표로 정리해보았다.
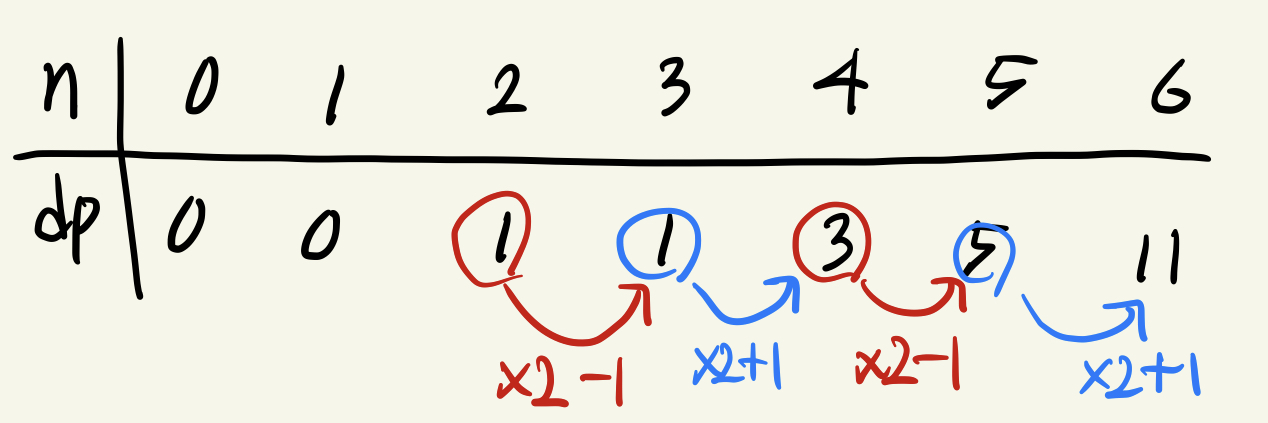
n이 짝수일 경우에는 n-1에서의 0 그룹의 2배보다 1 큰 값이 나왔고, n이 홀수일 경우에는 n-1에서의 0 그룹의 2배보다 1 작은 값이 나왔다. 이를 점화식으로 정의하면 다음과 같다.
dp[n]=dp[n-1]*2+1 (n%2==0)
dp[n]=dp[n-1]*2-1 (n%2==1)
이 점화식을 통해 코드를 작성하였다.
- n을 입력받는다.
- dp 리스트를 n+1의 크기로 선언하고 0으로 채운다.
- 2부터 n까지 반복하는 i에 대한 for문을 돌린다.
-> 만약 i%2가 0이 아닐 경우,
-->dp[i]를dp[i-1]*2-1로 갱신한다.
-> 그 외의 경우,
-->dp[i]를dp[i-1]*2+1로 갱신한다. dp[n]을 출력한다.
Code
n=int(input())
dp=[0 for _ in range(n+1)]
for i in range(2, n+1):
if i%2:
dp[i]=dp[i-1]*2-1
else:
dp[i]=dp[i-1]*2+1
print(dp[n])
