
그래프 (Graph)
그래프 이론에서 그래프란 객체의 일부 쌍들이 연관되어 있는 객체 집합 구조를 말한다.
오일러 경로
그래프 문제 하면 오일러 경로를 빼놓을 수 없다. n개의 섬과 m개의 다리가 있을 때 m개의 다리를 한번만 건너서 도달하는 것을 요구하는 문제이다. 오일러는 이 문제에서 모든 정점이 짝수개의 차수를 갖는다면 다리를 한번만 건너서 도달하는 것이 성립한다고 주장하였고 칼 히어홀저가 이를 수학적으로 증맹해냈다. 이를 오일러의 정리라고 부르고, 모든 간선을 한 번씩 방문하는 유한 그래프를 일컬어 오일러 경로라고 부른다.
해밀턴 경로
해밀턴 경로는 오일러 경로와 다르게 모든 간선을 한번씩 건너는 것이 아닌 모든 정점을 방문하는 경로를 말한다. 현재의 출발점으로 돌아오는 경로는 특별히 해밀턴 순환이라고 하고 이 중에서 최단 거리를 찾는 문제는 알고리즘 분야에서는 외판원 문제로도 유명하다. 외판원 문제는 각 도시를 모두 방문하고 돌아오는 가장 짧은 경로를 찾는 최단 거리 문제이다.
20개의 도시가 있는 외판원 문제를 브루트 포스 알고리즘으로 해결하면 20!개의 경로가 생긴다. 20!은 240경이 넘는 수이다. 외판원 문제를 다이나믹 프로그래밍 알고리즘을 활용하면 O(n^2*2^n)으로 최적화할 수 있고 n이 20일 경우에 약 4억 2천만 정도의 경로가 생긴다. 이 것도 매우 많지만 브루트 포스 알고리즘으로 해결하는 경우보다는 확실하게 적다.
그래프 순회
그래프 순회는 그래프 탐색이라고도 불리며 그래프의 각 정점을 방문하는 과정을 말한다. 그래프 순회에는 크기 깊이 우선 탐색 (DFS)와 너비 우선 탐색(BFS)의 2가지 알고리즘이 있다.
DFS의 경우에는 스택으로 구현하거나 재귀로 구현하고 백트래킹을 통해 뛰어난 효용을 보인다. BFS의 경우에는 큐로 구현하고 그래프의 최단 경로를 구하는 문제 등에 사용된다.
그래프를 표현하는 방법에는 인접 행렬과 인접 리스트의 2가지 방법이 있다. 인접 행렬은 행렬에서의 해당 위치의 값을 유의미한 값으로 갱신하는 방식으로 그래프를 표현하고, 인접 리스트는 출발 노드를 키로, 도착 노드를 값으로 표현하는 방식으로 그래프를 표현한다.
이번 시간에는 인접 리스트로 그래프를 표현하고 이에 대한 DFS, BFS 구현을 알아볼 것이다.
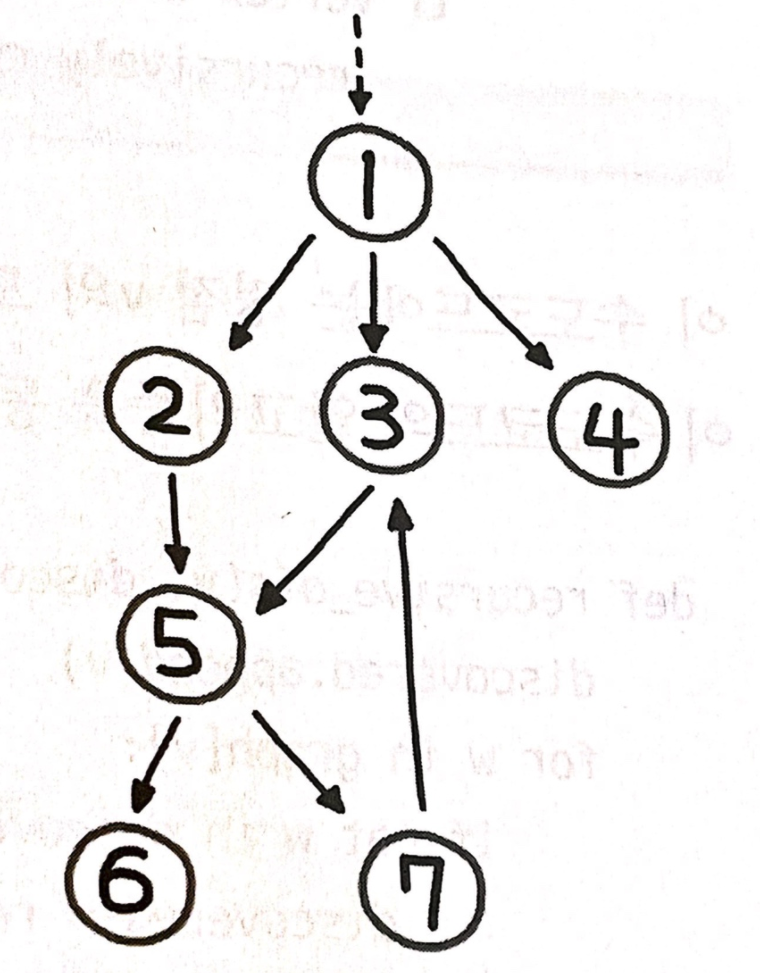
graph = {
1: [2, 3, 4],
2: [5],
3: [5],
4: [],
5: [6, 7],
6: [],
7: [3],
}DFS (깊이 우선 탐색)
일반적으로 DFS는 스택으로 구현하며, 재귀를 이용하면 좀 더 간단하게 구현할 수 있다. 코딩 테스트 시에도 재귀 구현이 더 선호되는 편이다.
재귀 구조로 구현
def recurvise_dfs(v, discovered=[]):
discovered.append(v)
for w in graph[v]:
if w not in discovered:
discovered = recursive_dfs(w, discovered)
return discovered방문했던 정점인 discovered를 계속 누적된 결과로 만들기 위해 리턴하는 형태만 받아오도록 처리했다. 위의 코드의 탐색 결과는 다음과 같다.
>>> f'recursive_dfs: {recursive_dfs(1)}'
'recursive_dfs: [1, 2, 5, 6, 7, 3, 4]'위의 그림을 손으로 DFS를 진행하면 이번 코드의 결과와 같이 1, 2, 5, 6, 7, 3, 4가 나오는 것을 알 수 있다.
스택을 이용한 반복 구조로 구현
def iterative_dfs(start_v):
discovered = []
stack = [start_v]
while stack:
v = stack.pop()
if v not in discovered:
discovered.append(v)
for w in graph[v]:
stack.append(w)
return discovered이와 같은 반복 구현은 앞서 코드가 길고 빈틈 없어보이는 재귀 구현에 비해 우아함은 떨어지지만 좀 더 직관적이기 때문에 이해하기 훨씬 쉽다. 실행 속도 또한 빠른 편이다. 이 코드의 결과는 다음과 같다.
f'iterative_dfs: iterative_dfs(1)}'
'iterative_dfs: [1, 4, 3, 5, 7, 6, 2]'같은 DFS임에도 재귀 구현과 반복 구현의 결과값의 순서가 다르게 나타난 것을 볼 수 있다. 재귀 DFS는 사전식 순서로 방문한 데에 반해 반복 DFS는 역순으로 방문했다. 스택으로 구현하였기 때문에 가장 마지막에 삽입된 노드부터 꺼내 반복하게 되기 때문이다.
BFS (너비 우선 탐색)
BFS는 DFS보다 쓰임새는 적지만 최단 경로를 구하는 다익스트라 알고리즘 등에 매우 유용하게 사용된다.
큐를 이용한 반복 구조로 구현
스택을 이용하는 DFS와 달리 BFS는 큐를 이용하여 구현한다.
def iterative_bfs(start_v):
discovered = [start_v]
queue = [start_v]
while queue:
v = queue.pop(0)
for w in graph[v]:
if w not in discovered:
discovered.append(w)
queue.append(w)
return discovered리스트 자료형을 사용했지만 pop(0)과 같은 큐 연산만 사용하였다. 좀 더 최적화 하기 위해서는 데크 자료형을 사용할 수 있다. 위 코드의 실행 결과는 다음과 같다.
f'iterative_bfs: {iterative_bfs(1)}'
'iterative_bfs: [1, 2, 3, 4, 5, 6, 7]'BFS의 경우 단계별 차례인 숫자 순으로 실행되었고 1부터 순서대로 각각의 인접 노드를 우선으로 방문하는 너비 우선 탐색이 잘 실행된 것을 확인할 수 있다.
BFS는 DFS와 다르게 재귀로 구현할 수 없다. 이 사실을 반드시 숙지해야 한다.
백트래킹 (Back tracking)
백트래킹은 해결책에 대한 후보를 구축해 나아가다가 가능성이 없다고 판단되는 즉시 후보를 포기해 정답을 찾아가는 범용적인 알고리즘으로 제약 충족 문제에 특히 유용하다.
DFS에 대해 공부하다보면 백트래킹이 항상 따라다닌다. 백트래킹은 DFS보다 좀 더 넓은 의미를 가진다. 백트래킹은 탐색을 하다가 더 갈 수 없으면 왔던 길을 되돌아가 다른 길을 찾는다는 데에서 유래되었다. 백트래킹은 DFS와 같은 방식으로 탐색하는 모든 방법을 뜻하며, DFS는 백트래킹의 골격을 이루는 알고리즘이다. 백트래킹은 주로 재귀로 구현되고 알고리즘마다 DFS 변형이 조금씩 일어나지만 기본적으로 모두 DFS의 범주에 속한다. 이는 부르트 포스와 유사하지만 한번 방문 후 가능성이 없는 경우에 즉시 후보를 포기한다는 점에서 부르트 포스보다는 훨씬 더 우아한 방식이라고 할 수 있다.
매우 큰 트리가 있을 때 브루트 포스로 전체 트리를 탐색한다면 매우 긴 시간이 소요될 것이다. 이 때 백트래킹을 이용하면 트리의 불필요한 부분을 버릴 수 있다. 이렇게 백트래킹에서 후보를 포기하는 것은 가지치기라고 하며 이렇게 불필요한 부분을 일찍 포기함으로써 탐색을 최적화할 수 있기 때문에 가지치기는 트리의 탐색 최적화 문제와도 관련이 깊다.
제약 충족 문제
백트래킹은 제약 충족 문제를 해결하기 위해 필수적으로 사용되는 알고리즘이다. 가지치기를 통해 제약 충족 문제를 최적화해주기 때문이다.
제약 충족 문제란 수많은 제약 조건을 충족하는 상태를 찾아내는 수학 문제를 말한다. 제약 충족 문제는 인공지능이나 경영 과학 분야에서 심도 있게 연구되고 있으며 합리적인 시간 내에 문제를 풀기 위해 휴리스틱과 조합 탐색 같은 개념을 함께 결합하여 문제를 풀이한다. 대표적인 제약 충족 문제로는 스도쿠가 있다. 스도쿠를 해결하기 위해서는 백트래킹을 통해 가지치기를 하여 최적화하는 과정이 필요하다. 스도쿠 외에도 십자말 풀이, 8퀸 문제, 4색 문제와 같은 퍼즐 문제와 배낭 문제, 문자열 파싱, 조합 최적화 문제 등 모두 제약 충족 문제에 해당한다.
LeetCode 200.Number of Islands
1을 육지로, 0을 물로 가정한 2D 그리드 맵이 주어졌을 때, 섬의 개수를 계산하라. (연결되어 있는 1의 덩어리 개수를 구하라.)
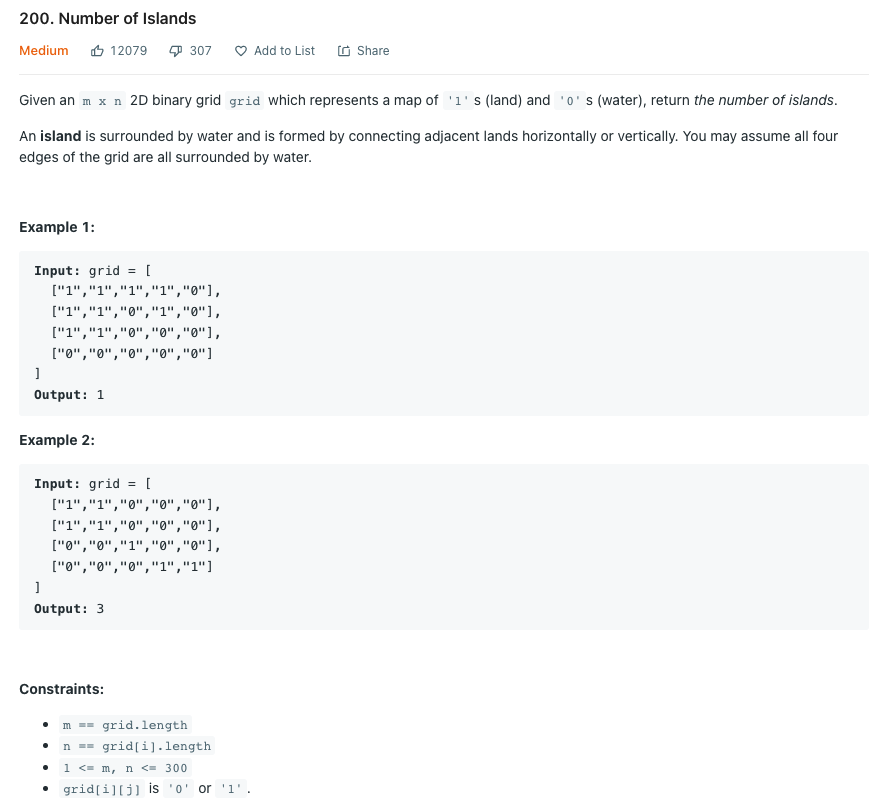
우선 혼자 힘으로 문제를 풀어보았다.
class Solution:
def numIslands(self, grid: List[List[str]]) -> int:
def dfs(h: str, w: str):
grid[h][w]='0'
dh=[0, 0, 1, -1]
dw=[1, -1, 0, 0]
for i in range(4):
nh=h+dh[i]
nw=w+dw[i]
if nh>=0 and nw>=0 and nh<len(grid) and nw<len(grid[0]) and grid[nh][nw]=='1':
dfs(nh, nw)
answer=0
for i in range(len(grid)):
for j in range(len(grid[0])):
if grid[i][j]=='1':
answer+=1
dfs(i, j)
return answer
DFS를 이용하여 접근하였다.
Solution 1 DFS로 그래프 탐색
이 문제는 쾨니히스베르크의 다리 문제처럼 반드시 그래프 모양이 아니더라도 그래프 형으로 변환해서 풀이할 수 있음을 확인해보는 좋은 문제이다. 페이스북을 비롯한 해외 기업에서 면접 시 자주 쓰이는 유명한 문제임과 동시에 국내 모 소셜커머스 회사의 실무 면접에서 화이트보드 코딩 문제로 출제된 문제이기도 하다. 입력값이 정확히 그래프는 아니지만 사실상 동서남북이 모두 연결된 그래프로 가정하고 동일한 형태로 처리할 수 있으며 네 방향 각각 DFS 재귀를 이용해 탐색을 끝마치면 1이 증가하는 형태로 육지의 개수를 파악할 수 있다.
여기서는 행렬 입력값인 grid의 행, 열 단위로 육지인 곳을 찾아 진행하다가 육지를 발견하면 그때부터 self.dfs()를 호출해 탐색을 시작한다.
DFS 탐색을 하는 dfs() 함수는 동서남북을 모두 탐색하면서 재귀호출하고 함수 상단에는 육지가 아닌 곳은 return으로 종료 조건을 설정해준다. 이렇게 재귀 호출이 백트래킹으로 모두 빠져 나오면 섬 하나를 발견한 것으로 간주한다. 이미 방문한 곳은 1이 아닌 값으로 마킹하여 방문 처리 해준다. 이 과정 또한 일종의 가지치기이다.
간혹가다가 또 다른 행렬을 생성해 그곳에 방문했던 경로를 저장하는 형태로 풀이하는 경우가 있는데 이 문제는 그렇게 할 필요가 없다. 별도의 행렬을 생성할 경우 공간 복잡도가 O(n)이 되기 때문에 별도의 행렬을 사용하지 않아도 된다고 판단될 때에는 사용하지 않는 것이 좋다.
dfs()함수를 빠져 나온 후에는 해당 위치에서 탐색할 수 있는 모든 육지를 탐색한 것이므로 카운트를 1 증가시킨다.
class Solution:
def numIslands(self, grid: List[List[str]]) -> int:
def dfs(i, j):
if i<0 or i>=len(grid) or j<0 or j>=len(grid[0]) or grid[i][j]!='1':
return
grid[i][j]=0
dfs(i+1, j)
dfs(i-1, j)
dfs(i, j+1)
dfs(i, j-1)
count=0
for i in range(len(grid)):
for j in range(len(grid[0])):
if grid[i][j]=='1':
dfs(i, j)
count+=1
return count
numIslands() 함수 내에 dfs() 함수 전체가 중첩 함수로 들어갔다. 이렇게 하면 numIslands() 함수에서만 dfs() 함수 호출이 가능한 제약이 생긴다. 그러나 중첩 함수는 부모 함수에서 선언한 변수도 유효한 범위 내에서 사용할 수 있다. 원래 다른 함수에서 변수를 사용하려면 globals()로 선언하는 등이 필요하지만 여기서 dfs()함수는 numIslands() 함수에서 선언된 변수를 자유롭게 사용 가능하다.
중첩 함수
중첩 함수란 함수 내에 위치한 또 다른 함수로, 바깥에 위치한 함수들과 달리 부모 함수의 변수를 자유롭게 읽을 수 있다는 장점이 있다. 실무에서 자주 쓰이지는 않지만 단일 함수로 해결해야 하는 경우가 잦은 코딩 테스트에서는 매우 자주 쓰이는 기능이다.
가변 객체의 경우에는 append(), pop() 등 여러가지 연산으로 조작도 가능하다. 그러나 재할당이 일어날 경우 참조 ID가 변경되어 별도의 로컬 변수로 선언되므로 이 부분은 주의가 필요하다.
리스트의 경우 가변 객체이기 때문에 중첩 함수 내에서 값을 변경하는 연산을 적용할 수 있다.
문자형의 경우 불변 객체이기 때문에 값을 변경할 수 없다. 중첩 함수 내에서 값의 변경을 원할 경우 새롭게 재할당하게 되는데 이때 객체의 참조 ID가 변경되어 서로 다른 변수가 된다. 중첩 함수의 경우에는 함수 내에서만 사용 가능한 새로운 로컬 변수로 선언되며 여기서 수정된 값, 즉 재할당된 값은 부모 함수에서는 반영되지 않으므로 주의가 필요하다.
LeetCode 17.Letter Combinations of a Phone Number
2에서 9까지 숫자가 주어졌을 때 전화 번호로 조합 가능한 모든 문자를 출력하라.

Solution 1 모든 조합 탐색
이 문제는 전체를 탐색하여 풀이할 수 있다. 항상 전체를 탐색해야 하고 가지치기 등으로 최적화할 수 있는 문제는 아니기 때문에 어떻게 풀이하든 결과는 비슷하다. 가능한 경우의 수를 모두 조합하는 형태로 전체를 탐색한 후 백트레킹하면서 결과를 조합할 수 있다.
2 a b c
3 d e f
result=[ad, ae, af, bd, be, bf, cd, ce, cf]각 자릿수에 해당하는 키판 배열을 DFS로 탐색하면 결과가 완성된다. 키판 배열을 우선 딕셔너리로 정의해주고 난 뒤에 DFS로 탐색을 진행한다.
digits='23'
path=''
dic={'2': 'abc', '3': 'def', '4': 'ghi', '5': 'jkl', '6': 'mno', '7': 'pqrs', '8': 'tuv', '9': 'wxyz'}
for i in range(index, len(digits)):
for j in dic[digits[i]]:
dfs(i+1, path+1)입력값을 자릿수로 쪼개어 반복하고, 숫자에 해당하는 모든 문자열을 반복하면서 문자 단위로 재귀 탐색을 진행한다. dfs() 함수는 자릿수가 동일할 때까지 재귀 호출을 반복하다가 끝까지 탐색하면 결과를 추가하고 반환한다. 이렇게 하면 모든 경우의 수를 DFS로 탐색하고 백트래킹으로 결과를 조합하면서 리턴하게 된다.
class Solution:
def letterCombinations(self, digits: str) -> List[str]:
def dfs(index, path):
if len(path) == len(digits):
result.append(path)
return
for i in range(index, len(digits)):
for j in dic[digits[i]]:
dfs(i+1, path+j)
if not digits:
return []
dic={'2': 'abc', '3': 'def', '4': 'ghi', '5': 'jkl', '6': 'mno', '7': 'pqrs', '8': 'tuv', '9': 'wxyz'}
result=[]
dfs(0, '')
return result
LeetCode 46.Permutations
서로 다른 정수를 입력받아 가능한 모든 순열을 리턴하라.
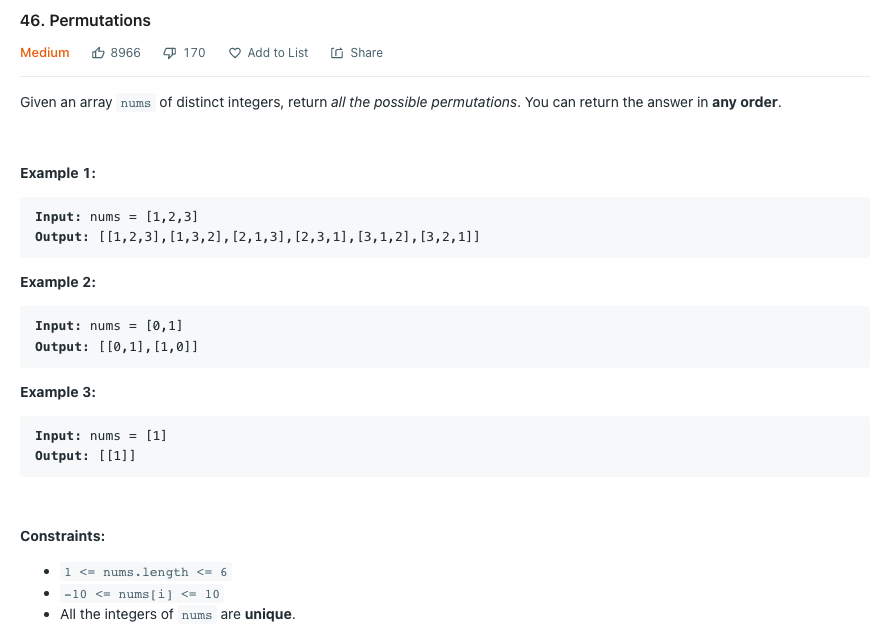
Solution 1 DFS를 활용한 순열 생성
모든 순열을 구하기 위해서는 모든 가능한 경우를 그래프 형태로 나열한 결과라고 할 수 있다. 이를 그래프로 나타내면 다음과 같다.
A(0, 3) []
A(1, 3) [1] [2] [3]
A(2, 3) [1,2] [1,3] [2,1] [2,3] [3,1] [3,2]
A(3, 3) [1,2,3] [1,3,2] [2,1,3] [2,3,1] [3,1,2] [3,2,1]위의 그래프에서 리프 노드, 즉 A(3, 3)의 모든 노드가 순열의 최종 결과이다. 레벨이 증가할수록 자식 노드의 개수가 점점 작아지는 것을 확인할 수 있다. 만약 입력값이 5였다면 자식 노드의 개수는 5x4x3x3x1이 되었을 것이다.
def dfs(elements):
if len(elements)==0:
result.append(prev_elements[:])
for e in elements:
next_elements = elements[:]
next_elements.remove(e)
prev_elements.append(e)
dfs(next_elements)
prev_elements.pop()이전 값을 하나씩 덧붙여 계속 재귀 호출을 진행하다 리프 노드에 도달한 경우(len(elements)==0의 경우) 결과를 하나씩 담는다. 이때 주의할 점은 결과를 추가할 때 prev_elements[:]로 처리해야 한다는 점이다. 파이썬은 모든 객체를 참조하는 형태로 처리되기 때문에 만약 results.append(prev_elements)를 하게 되면 결과 값이 추가되는 것이 아닌 prev_elements에 대한 참조가 추가되고 이 경우 참조된 값이 변경될 경우 같이 바뀌게 된다. 따라서 값을 복사하는 형태로 참조 관계를 갖지 않도록 처리해야 한다.
class Solution:
def permute(self, nums: List[int]) -> List[List[int]]:
results = []
prev_elements = []
def dfs(elements):
if len(elements)== 0:
results.append(prev_elements[:])
for e in elements:
next_elements = elements[:]
next_elements.remove(e)
prev_elements.append(e)
dfs(next_elements)
prev_elements.pop()
dfs(nums)
return results
Solution 2 itertools 모듈 사용
파이썬에는 itertools라는 모듈이 존재한다. itertools 모듈은 반복자 생성에 최적화된 효율적인 기능들을 제공하므로 실무에서는 알고리즘을 직접 구현하기보다는 가능하다면 itertools 모듈을 사용하는 편이 낫다. 이미 잘 구현된 라이브라리라 직접 구현함에 따른 버그 발생 가능성이 낮고, 무엇보다 효율적으로 설계된 C라이브러리라 속도에도 이점이 있다.
물론 온사이트 인터뷰 시 순열 구현을 풀이하는데 itertools 모듈을 사용하겠다고 하면 라이브러리르 쓰지 말고 구현하라는 주문을 받을 가능성이 높다. 그러나 온라인 테스트의 경우 별도의 제약 사항이 없다면 사용하지 않을 이유가 없다. 주석으로 "구현의 효율성, 성능을 위해 사용했다." 등의 설명을 달아둔다면 더할나위 없이 좋다. 대면 인터뷰 시에도 면접관에게 한 번쯤 어필할 필요가 있다. "이런 라이브러리가 있고, 지금은 알고리즘을 직접 풀이 중이라 사용하지 않겠지만 실무에서는 사용하지 않을 이유가 없다."는 정도로 가볍게 어필해볼 필요가 있다. 항상 그렇듯 잘 만들어진 라이브러리를 사용하면 풀이가 매우 간단해진다.
class Solution:
def permute(self, nums: List[int]) -> List[List[int]]:
return list(itertools.permutations(nums, len(nums)))
객체 복사
파이썬의 중요한 특징 중 하나는 모든 값이 객체로 존재한다는 점이다. 숫자, 문자까지도 모두 객체이다. 숫자, 문자가 리스트, 딕셔너리와 다른점은 불변 객체라는 차이 뿐이다. 그러다 보니 별도로 값을 복사하지 않는 한, 변수에 값을 할당하는 모든 행위는 값 객체에 대한 참조가 된다. 이 말은 참조가 가리키는 원래의 값을 변경하면 모든 참조, 즉 모든 변수의 값 또한 함께 변경된다는 말이기도 하다. 참조가 되지 않도록 값 자체를 복사하려면 어떻게 해야할까? 가장 간단한 방법은 [:]로 처리하는 방법이다.
>>> a=[1,2,3]
>>> b=a
>>> c=a[:]
>>> id(a), id(b), id(c)
(4362781552, 4362781552, 4361580048)[:]로 처리한 변수 c는 혼자 다른 ID를 가지는 것을 확인할 수 있다. 이외에도 좀 더 직관적으로 처리하는 방법은 다음과 같이 명시적으로 copy() 메소드를 사용하는 방법이다.
>>> d=a.copy()
>>> id(a), id(b), id(c), id(d)
(4362781552, 4362781552, 4361580048, 4363974768)이 경우 변수 d 또한 다른 ID를 가지게 된다. 값이 복사되어 새로운 객체가 되었음을 확인할 수 있다. 단순한 리스트의 경우 [:]나 copy()로 쉽게 처리가 가능하지만 복잡한 리스트의 경우에는 copy.deepcopy()로 처리해야 한다.
>>> import copy
>>> a=[1,2,[3, 5], 4]
>>> b=copy.deepcopy(a)
>>> id(a), id(b), b
(4480589512, 4481610824, [1, 2, [3, 5], 4])이처럼 리스트 내에 리스트를 갖는 중첩된 리스트도 deepcopy()를 사용하면 문제없이 값을 복사할 수 있으며 다른 ID를 갖는다.
To be continue ...
